1192. Critical Connections in a Network - kumaeki/LeetCode GitHub Wiki
1192. Critical Connections in a Network
There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some server unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
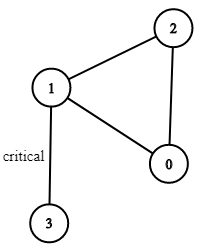
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.
Constraints:
- 1 <= n <= 10^5
- n-1 <= connections.length <= 10^5
- connections[i][0] != connections[i][1]
- There are no repeated connections.
看完题目直接放弃.开始找答案.
-
用timeArr来存储从首次到达当前节点的时间(每经过一个节点增加1), 这里我们固定从0开始, 其实从任意点开始都可以
-
对于每一个节点,我们都去计算到达它的所有后续节点的时间的最小值 min,和当前节点比较
如果min 大于 当前节点的时间, 那么存在环(后续节点可以先于当前节点被访问到)
如果min 等于 当前节点的时间, 那么存在环, 但是这个环是通过当前节点与其他部分相连接
如果min 小于 当前节点的时间, 那么当前节点和其父节点的连接就是 critical connection(如果有父节点的话)
上面等于的部分,有一点绕,可以尝试通过下面这个例子想明白.
Input: n = 6, connections = [[0,1],[1,2],[2,0],[1,3],[3,4],[4,5],[5,3]]
class Solution {
// 到达当前节点的时间
static int ti = 1;
public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
// 定义长度为n的List型数组,graph[i]表示从节点i出发可以到达的节点
List[] graph = new List[n];
for(int i = 0; i < n; i++)
graph[i] = new ArrayList<Integer>();
// 填充graph(非有向图,所以要双向填充)
for(List<Integer> con : connections){
graph[con.get(0)].add(con.get(1));
graph[con.get(1)].add(con.get(0));
}
// 到达所有节点的时间
int[] timeArr = new int[n];
// 结果
List<List<Integer>> res = new ArrayList<List<Integer>>();
getMinTime(graph, timeArr, 0, -1, res);
return res;
}
// 返回到达cur的最小到达时间
private int getMinTime(List[] graph,int[] timeArr, int cur, int parent, List<List<Integer>> res){
// 如果当前节点计算过, 那么直接返回
if(timeArr[cur] > 0)
return timeArr[cur];
// 默认值设置为ti, ti递增1
timeArr[cur] = ti++;
// cur所有后续节点的最小到达时间默认为Integer的最大值
int min = Integer.MAX_VALUE;
// 遍历cur的所有可以到达的节点
for(int next : (List<Integer>)graph[cur]){
// 父节点排除计算,因为在父节点的结算周期中已经计算过这个connection
if(next == parent)
continue;
//递归计算到达next的最小时间
int nextTime = getMinTime(graph, timeArr, next, cur, res);
min = Math.min(min, nextTime);
}
// 如果后续所有节点的到达时间都大于当前节点,并且存在父节点, 那么父接到到当前节点的connection 就是critical
if(min >= timeArr[cur] && parent != -1)
res.add(Arrays.asList(parent, cur));
// 返回最小到达时间
return Math.min(timeArr[cur], min);
}
}