0684. Redundant Connection - kumaeki/LeetCode GitHub Wiki

0684. Redundant Connection

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

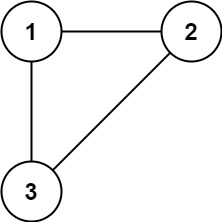
Input: edges = [[1,2],[1,3],[2,3]]

Output: [2,3]

Example 2:

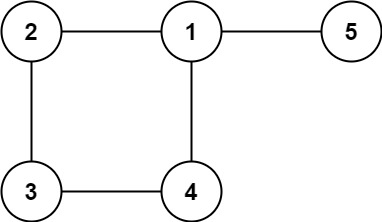
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]

Output: [1,4]

Constraints:

  • n == edges.length
  • 3 <= n <= 1000
  • edges[i].length == 2
  • 1 <= ai < bi <= edges.length
  • ai != bi
  • There are no repeated edges.
  • The given graph is connected.

解法1

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        
        int n = edges.length;
        // 用map来构建图, 初始为空
        Map<Integer, List<Integer>> graph = new HashMap<>(n);
        
        // 从第一条边开始构建图
        for(int[] e : edges){
            // 在当前边加入图之后的访问记录, 每次新加入一条边都清空
            boolean[] isVisited = new boolean[n + 1];
            // 如果两个节点已经存在于图中, 并且在当前边加入图之前是相互连通的, 那么把当前边加入之后就可以形成cycle
            // 返回结果
            if(graph.containsKey(e[0]) && graph.containsKey(e[1]) && helper(isVisited, graph, e[0], e[1]))
                return e;
            
            // 否则, 将边加入图中, 继续计算
            if(!graph.containsKey(e[0]))
                graph.put(e[0], new ArrayList<Integer>());
            if(!graph.containsKey(e[1]))
                graph.put(e[1], new ArrayList<Integer>());
            graph.get(e[0]).add(e[1]);
            graph.get(e[1]).add(e[0]);
        }
        return new int[]{0, 0};
    }
    
    // 深度优先, 判断从start是否可以到达end
    private boolean helper(boolean[] isVisited, Map<Integer, List<Integer>> graph, int start, int end){
        
        // 如果start节点没有被访问过, 那么继续计算
        // 因为是无向图, 需要考虑反向连接的问题,所以要用isVisited来排除1 -> 2 -> 1这种通过同一条边反向重复计算
        if(!isVisited[start]){
            isVisited[start] = true;
            if(start == end)
                return true;
            for(int next : graph.get(start))
                if(helper(isVisited, graph, next, end))
                    return true;
        }
        
        // 如果start节点已经被访问过, 结束计算
        return false;
    }
}
⚠️ **GitHub.com Fallback** ⚠️