Working with Vectors - juniverse1103/ARKitStudy GitHub Wiki
Working with Vectors
Use vectors to calculate geometric values, calculate dot products and cross products, and interpolate between values.
Overview
-
A vector is comparable to a fixed-length array containing integer or floating-point values.
-
The simd library provides support for small vectors, that is, vectors that contain up to eight double-precision or sixteen single-precision values.
-
You can use vectors to represent data such as:
- Color
- R,G,B, and Alpha
- Position
- Coordinates in 2D or 3D space
- Color
-
simd library example for two vectors containing 4 elements
let a = simd_float4(x: 2, y: 4, z: 5, w: 8) let b = simd_float4(x: 5, y: 6, z: 7, w: 8) -
Sum vectors with + operator
let c = a + b // c = (7.0, 10.0, 12.0, 16.0)
Calculate Luminance
-
Calculate the luminance of a color by multiplying each of its red, green, and blue color channels by a certain coefficient, and create a grayscale representation of the color by adding the three products together.
-
Below code uses Rec.709 luma coefficients for the color-to-grayscale conversion.
-
func lumaForColor(red: Float, green: Float, blue: Float){ let luma = (red*0.2126) + (green*0,7152) + (blue*0.0722) return luma } -
simd library simflities this code by treating the color and the coefficients as vecotrs, and returning the dot product of the vectors.
-
let rec709Luma = simd_float3(0.2126, 0.7152, 0.0722) func lumaForColor(red: Float, green: Float, blue: Float){ let luma = simd_dot(rec709Luma, simd_float3(red,blue,green)) return luma }
Calculate Length and Distance
- Calculate the distance between two points using the Pythagorean theorem.
- simd library provides functions for calcuating length and distance in two, three and four dimensions.
Calculate Length
- Length functions, e.g.
simd_length(_:)return the length of a vector.
Calculate Distance
-
Distance functions, e.g.
simd_distance(_:_:)return the distance between two vectors. -
let a = simd_float2(x:3, y:4) let b = simd_float2(x:0, y:0) let dist = simd_distance(a,b) let len = simd_length(a)
Compare Distances
- Comparing vectors' distance or length with comparing the square of those.
let target = simd_float2(x:5, y:2)
if simd_distance_squared(a, target) < simd_distance_squared(b,target){
// 'a' is closest to 'target'
} else{
// 'b' is closest to 'target'
}
Calculate Reflection and Refraction Vectors
-
The simd library provides functions for calculating vectors that describe reflections and refractions in two-, three-, and four- dimensional space.
-
The image below shows:
- An incident ray, described by the vector
simd_double2(x:1.5, y:-1), traveling toward the center of the image. - A normal, described by the vector
simd_double2(x:0, y:1), that's perpendicular to the interface between the two media. - The reflected ray, computed by simd, traveling away from the center of the image.
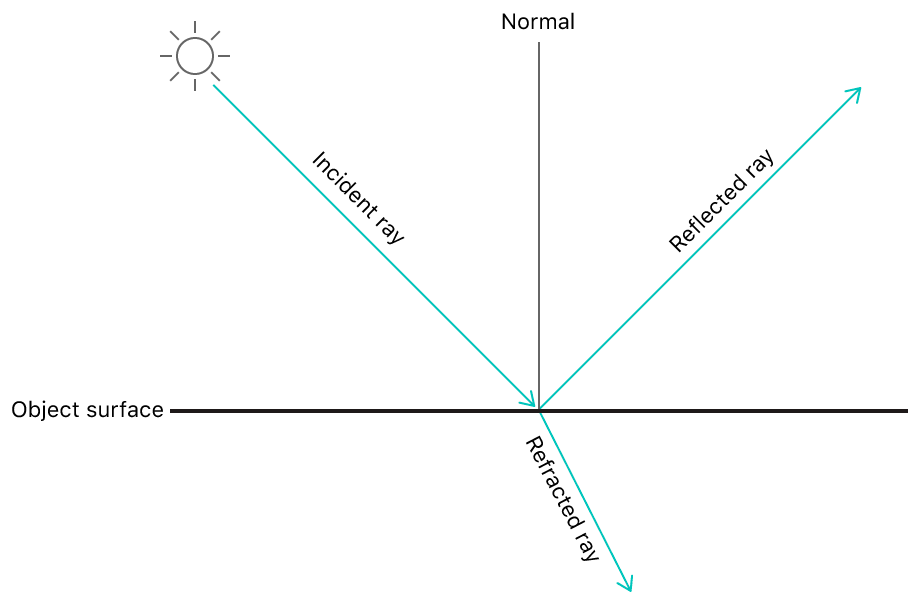
- An incident ray, described by the vector
Normalize Vectors
-
Normalize the vectors(calculate a vector with the same direction as the original, but with a length of 1) passed to the reflect and refract functions to achieve the correct results.
-
Given the values above, the code defines normalized vectors for the incident ray and normal:
let incident = simd_normalize(simd_double2(x: 1.5, y: -1)) let normal = simd_normalize(simd_double2(x: 0, y: 1))
Calculate Reflection
-
You get the reflected vector with
simd_reflect(_:_:): -
let reflected = simd_reflect(incident, normal)
Calculate Refraction
-
For the refraction function, pass an additional parameter(eta) that models the index of refraction for physicacl materials:
-
let air = 1.0 // refractive index for air let glass = 1.5 // refractive index for glass let refracted = simd_refract(incident, normal, air/glass)
Calculate the Normal of a Triangle
-
The normal of a triangle is the vector perpendicular to its surface.
-
Use the simd library's cross product function to calculate the normal of a triangle.
-
This is a common task in 3D graphics programming and is used when calculating the shading of surfaces.
-
In the image below, the triangle's normal is shown as a red line that's perpendicular to the surface of the triangle.

The following code defines the three vertices of the triangle:
let vertex1 = simd_float3(-1.5, 0.5, 0) let vertex2 = simd_float3(1,0,3) let vertex3 = simd_float3(0.5,-0.5, -1,5) -
First step in calculating the normal of the triangle is to create two vectors defined by the difference between the vertices - representing two sides of the triangle:
-
let vector1 = vertex2 - vertex3 let vector2 = vertex2 - vertex1 -
The simd_cross function returns the vector that's perpendicular to the two vectors. Normalize the result to get unit vector of the normal of the triangle to get only the direcitonl.
-
let normal = simd_normalize(simd_cross(vector1, vector2))
Interpolate Between Values
- Interpolation adds new, intermediate data points between known values.
- The simd library provides functions to linearly and smoothly interpolate between scalar and vector values.
- Smooth interpolation is commonly used in animation, and you can, for example, use the functions described below to define the timingFunction of a SpriteKit action.
- example illustration of linear and smooth interpolation between boundary values.

Linearly interpolate
-
Linear interpolation is provided by the
simd_mixfunction. -
The first two parameters specify the range, and the third parameter specifies the normalized(between 0 and 1) position in the range.
-
The following code shows how to populate an array with 1024 elements. The first element in the array has a value of -100, and the last element of the array has a value of 100.
-
Intermediate elements linearly interpolate between the first and last values:
-
let linear: [Float] = stride(from:0.0, to: 1.0, by: 1/1024).map{ x in return simd_mix(-100,100,x) }
Smoothly Interpolate
-
Smooth interpolation is provided by the simd_smoothstep function.
-
This function uses Hermite interpolation based on the following code:
-
simd_double4 simd_smoothstep(simd_double4 edge0, simd_double4 edge1, simd_double4 x){ simd_double4 t = simd_clamp((x-edge0)/(edge1-edge0),0,1); return t*t*(3-2*t); } -
The first two parameters specify the range, and the third parameter specifies the position in the range.
-
Unlike the mix function, the position isn't normalized, but the return value is.
-
The following code shows how to populate an array with 1024 elements.
-
The first element in the array has a value of 0, and the last element of the array has a value of 1. Intermediate elements smoothly interpolate between the first and last valued:
-
let smooth:[Float] = (-512..<512).map{ x in return simd_smoothstep(-512,512,Float(x)) }