数理化札记ツイ(4): 如何得到超大之数续编 - johanzumimvon/1 GitHub Wiki
TREE(4)是指, 准备4种颜色, 红、黄、绿、蓝, 然後先用红色画出树, 之後第2颗~第TREE(4)颗树, 也就是[TREE(4)−1]颗树是用黄、绿、蓝色着色.
士大夫發明的大数数学运算, 虽然比康威链、BEAF链粗糙些, 但是相比於白色人种發明的康威链、BEAF链, 士大夫的發明更加形象直观.
基本等级正向运算
| 等级 | 种类 | 意味 | 反向 |
|---|---|---|---|
| 0 | y=x | y=x | |
| 1 | 後继 | y=x+1 | y=x−1 |
| 2 | 加 | y=x+a | y=x−a |
| 3 | 乘 | y=x·a=ax | y=x÷a |
| 4 | 指数 | y=aˣ | |
| 连幂 | y=a↑↑x | 暂无 |
其中, 後继运算可记作y=フ[x], 即
フ[x]=x+1
フ[フ[x]]=x+1+1=x+2
フ[x]的反函数或者逆运算为y=x−1
ラ[a|x]=a↑⁽ˣ⁾a
ラ₂[a|x]=ラ[a|ラ[a|ラ[a|ラ[a|ラ[a|……ラ[a|a]]]]]]
迭代x次
比如
ラ₂[9|4]
=ラ[9|ラ[9|ラ[9|ラ[9|9]]]]
ラₙ[a|x]=ラₙ₋₁[a|ラₙ₋₁[a|ラₙ₋₁[a|ラₙ₋₁[a|ラₙ₋₁[a|x]……ラₙ₋₁[a|a]]]]]
迭代x次
比如
ラ₁₉₈₉[64|5]
=ラ₁₉₈₈[64|ラ₁₉₈₈[64|ラ₁₉₈₈[64|ラ₁₉₈₈[64|ラ₁₉₈₈[64|64]]]]]
φ(a|x)=ラₓ[a|a]
φ₂(a|x)=φ(a|φ(a|φ(a|φ(a|φ(a|……φ(a|a))))))
迭代x次
比如
φ₂(9|4)
=φ(9|φ(9|φ(9|φ(9|9))))
φₙ(a|x)=φₙ₋₁(a|φₙ₋₁(a|φₙ₋₁(a|φₙ₋₁(a|φₙ₋₁(a|……φₙ₋₁(a|a))))))
迭代x次
ア[a|x]=φₓ(a|a)
ア₂[a|x]=ア[a|ア[a|ア[a|ア[a|ア[a|……ア[a|a]]]]]]
迭代x次
アₙ[a|x]=アₙ₋₁[a|アₙ₋₁[a|アₙ₋₁[a|アₙ₋₁[a|アₙ₋₁[a|x]……アₙ₋₁[a|a]]]]]
迭代x次
イ[a|x]=アₓ[a|a]
イ₂[a|x]=イ[a|イ[a|イ[a|イ[a|イ[a|……イ[a|a]]]]]]
迭代x次
イₙ[a|x]=イₙ₋₁[a|イₙ₋₁[a|イₙ₋₁[a|イₙ₋₁[a|イₙ₋₁[a|x]……イₙ₋₁[a|a]]]]]
迭代x次
기[a|x]=イₓ[a|a]
기₂[a|x]=기[a|기[a|기[a|기[a|기[a|……기[a|a]]]]]]
迭代x次
기ₙ[a|x]=기ₙ₋₁[a|기ₙ₋₁[a|기ₙ₋₁[a|기ₙ₋₁[a|기ₙ₋₁[a|x]……기ₙ₋₁[a|a]]]]]
迭代x次
a↑b=aᵇ
a↑↑2=a↑a=aᵃ
a↑↑3=a↑a↑a=
a↑↑4=a↑a↑a↑a=
a↑↑↑2=a↑↑a
a↑↑↑3=a↑↑a↑↑a=a↑↑[a↑↑a] 超运算的右结合律
a↑⁽³⁾n=a↑↑↑n
a↑⁽⁴⁾n=a↑↑↑↑n
a↑⁽⁵⁾n=a↑↑↑↑↑n
a↑⁽⁶⁾n=a↑↑↑↑↑↑n
罗运算(又名拉运算)ラ[a|x]是指a与a连x个高德纳箭头的运算, 也就是a与a的x阶高德纳运算.
罗运算是高德纳运算的上层次形式, 罗运算又名朱明远运算.
比如
ラ[89|4]=89↑↑↑↑89
二階罗算ラ₂[a|x]是指a被ラ函数迭代了x次, 比如
ラ₂[89|4]
=ラ[89|ラ[89|ラ[89|ラ[89|89]]]]
ラ₂[7|9]
=ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|7]]]]]]]]]
=ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|ラ[7|7↑↑↑↑↑↑↑7]]]]]]]]
ㇰ゙ラハㇺ数可以被标记作ラ₂[3|64, 4]. 其中, 3是指被运算的数; 64是指被被ラ[3|x]迭代了64次; 4是指第一次被迭代时的值为ラ[3|4], 即3↑↑↑↑3
g(64)
=ラ₂[3|64, 4]
=ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|4]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]
=ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|3↑↑↑↑3]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]
=ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|3↑↑↑3↑↑↑3↑↑↑3]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]
=ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|3↑↑↑3↑↑↑[3↑↑3↑↑3↑↑3]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]
=ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|ラ[3|3↑↑↑[3↑↑↑[3↑↑3↑↑7625597484987]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]
其中, 3↑↑7625597484987相当于这个数取自然对数ln(x)取了7625597484987次, 才能得到接近1.22的数. 也就是
ln7625597484987(3↑↑7625597484987)≈1.22
即, 我每秒对3↑↑7625597484987取30次自然对数迭代(按键盘不动), 我至少需要8060年又2.444月方能把这个数变成屈指可数.
3↑3=27
3↑↑3=7625597484987
3↑↑↑3=3↑↑7625597484987相当于按键盘取自然对数用了8060年.
之于3↑↑↑↑3, 我说不出来有多大了.
然而3↑↑↑↑3又要被ラ[3|x]迭代63次. 感觉整个人都超级不可思议了.
不过与TREE(3)相比, 葛立恒数又是小到难以置信. 即使是在本条目中, 葛立恒数也仅仅是第5阶运算而已.
葛立恒数大小位于第5階运算罗运算的等级上, 但是葛立恒数要远远见绌于TREE(3)、第6阶运算毘运算、第7阶运算阿运算、第八阶运算伊运算、第九阶运算基运算所得到的结果.
士大夫对江西钉子户(金刚户, diamond户)的微看法
江西钉子户後悔, 可能是因为钉子户确定认识到自己错了, 也可能是因为忠汞改变了以前暴戾拆迁的态度. 但不论如何, 忠汞脑子裡只有维稳(ヱヱㇴ).
士大夫认为, 即使在未来世, 忠汞承认自己發动了六四大屠杀、迫害中国家庭教会, 那也是中国共产党的金蝉脱壳般推卸责任的技能, 并不是忠汞真的变法悔改了.
因为忠汞的哲学就是唯物辩证法, 认为宇宙的一切都是矛盾, 都是需要被战天斗地的对象, 反正忠汞不论如何, 都改不了牠的罗刹本德!
在国际关系上, 忠汞依靠唯物辩证法, 认为“没有永远的朋友; 只有永远的利益”, 所以中华人民共和国活该没朋友!
n階罗算ラₙ[a|x]是指a被(n−1)階ラ函数迭代了x次, 比如
ラ₄₆₉₈₉₁[64|5]=ラ₄₆₉₈₉₀[64|ラ₄₆₉₈₉₀[64|ラ₄₆₉₈₉₀[64|ラ₄₆₉₈₉₀[64|ラ₄₆₉₈₉₀[64|64]]]]]
![ラ[64|1989]](https://private-user-images.githubusercontent.com/167794740/405064098-3bf0cb52-0edc-427d-821e-947ff1ad2517.jpg?jwt=eyJ0eXAiOiJKV1QiLCJhbGciOiJIUzI1NiJ9.eyJpc3MiOiJnaXRodWIuY29tIiwiYXVkIjoicmF3LmdpdGh1YnVzZXJjb250ZW50LmNvbSIsImtleSI6ImtleTUiLCJleHAiOjE3NjEwMDg2NjcsIm5iZiI6MTc2MTAwODM2NywicGF0aCI6Ii8xNjc3OTQ3NDAvNDA1MDY0MDk4LTNiZjBjYjUyLTBlZGMtNDI3ZC04MjFlLTk0N2ZmMWFkMjUxNy5qcGc_WC1BbXotQWxnb3JpdGhtPUFXUzQtSE1BQy1TSEEyNTYmWC1BbXotQ3JlZGVudGlhbD1BS0lBVkNPRFlMU0E1M1BRSzRaQSUyRjIwMjUxMDIxJTJGdXMtZWFzdC0xJTJGczMlMkZhd3M0X3JlcXVlc3QmWC1BbXotRGF0ZT0yMDI1MTAyMVQwMDU5MjdaJlgtQW16LUV4cGlyZXM9MzAwJlgtQW16LVNpZ25hdHVyZT0xMTllMGM4ZjU3ZGYzOTU4OGI1NzcyMDc4ZmNmOTRlOGRiMTkyNTBjMTc2MmU3YzBiMzBhN2U5NjIwM2MzMjNmJlgtQW16LVNpZ25lZEhlYWRlcnM9aG9zdCJ9.YBktiLe5riBe-9eeMcXnQziFxRHZEK7mRKP7MquHP1k)
大数的运算可被系统地写作ラ[a, b|c|d, h], 其中a表示运算的等级; b表示运算的亚等级; c表示要用什么数计算; d表示迭代次数; h表示第一次迭代所用的值.
比如葛立恒数可记作ラ[5, 2|3|64, 4];
n≥2时有
ラ[5, n|c|b, a]=ラₙ[c|b, a]
ラ[6, n|c|b, a]=φₙ(c|b, a)
ラ[7, n|c|b, a]=アₙ[c|b, a]
ラ[8, n|c|b, a]=イₙ[c|b, a]
ラ[9, n|c|b, a]=기ₙ[c|b, a]
更加简洁的形式是ラ[n|c|b], 就是在n階运算中, c被迭代了b次, 比如
ラ[9|64|4]=기[64|4]
又比如,
ラ₂[9|64|4]=기₂[64|4]=기[64|기[64|기[64|기[64|64]]]]
| n | n階数 |
|---|---|
| 0 | 0~12 |
| 1 | (12+ε)~13 |
| 2 | (13+ε)~24 |
| 3 | (24+ε)~144 |
| 4 | (144+ε)~8916100448256 |
| 5 | (8916100448256+ε)~12↑↑↑↑↑↑↑↑↑↑↑↑12 |
| 6 | [ラ[12ㅣ12]+ε]~ラ₁₂[12ㅣ12] |
| 7 | [φ(12ㅣ12)+ε]~φ₁₂(12ㅣ12) |
| 8 | [ア[12ㅣ12]+ε]~ア₁₂[12ㅣ12] |
| 9 | [イ[12ㅣ12]+ε]~イ₁₂[12ㅣ12] |
| 10 | [기[12ㅣ12]+ε]~기₁₂[12ㅣ12] |
| 11 | [ラ[10ㅣ12ㅣ12]+ε]~ラ₁₂[10ㅣ12ㅣ12] |
| 12 | [ラ[11ㅣ12ㅣ12]+ε]~ラ₁₂[11ㅣ12ㅣ12] |
人们所认识的天文数字, 大多属于4阶或者5阶.
这样的话, 只要标明出某个数的数阶是多少, 就能轻鬆地知道某个大数的等级如何. 比如G(64)的数值恰好为ラ₂[3|64, 4], 且φ(2|3)<ラ₂[3|64, 4]<φ(2|64), 位于第五阶运算罗运算中, 那么G(64)是第6阶数.

下面定義一函数, 叫做大纪元函数, 其在f(n)的取值是二个n经过第n阶运算得到的结果:
f(0)=0
f(1)=1+1
f(2)=2+2
f(3)=3·3
f(4)=4⁴
f(5)=ラ[5|5]=5↑↑↑↑↑5
f(6)=φ(6|6)=ラ₆[6|6]
f(7)=ア[7|7]=φ₇(7|7)
f(8)=イ[8|8]=ア₈[8|8]
f(9)=기[9|9]=イ₉[9|9]
也就是f(n)对应n与n的第n阶运算.
函数值
| n | f(n) |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 9 |
| 4 | 256 |
fₙ(x)=f(f(f(f(f(……f(x)))))), 比如
f₃(64)=f(f(f(64)))
F₂(x)=
F₂(64)=
F₃(64)=
F₄(64)=
F₄(x)=
etc
フ₂(x)=
フ₂(64)=
フ₃(64)=
フ₄(64)=
フ₄(x)=
对于大纪元函数f(x), 令
a₁=f(64)
a₂=f₆₄(64)=f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(f(64))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
a₃=F₆₄(64)
a₄=フ₆₄(64)
aₙ=フ[n, 64, 64]
之後得到的a(64)一定是有史以来最大的数字.
| x | y=ntd(x) |
|---|---|
| 1 | f(1)=2 |
| 2 | F₂(2) |
| 3 | フ₃(3) |
| 4 | フ[4, 4, 4] |
| 5 | フ[5, 5, 5] |
| 6 | フ[6, 6, 6] |
10¹⁰⁰、TREE(3)等等, 但是我的函数也许在f(8)就能超越人类有史以来提出的所有的数, 比如TREE(3)、拉约数、bigfoot、fish(7)等等, 即使对函数运算规则稍作修改亦是如是.
我的函数比康威链定義更加简单明瞭, 但增长起来更为难以置信.
| 种类 | 增长等级 |
|---|---|
| y=x⁻ᵃ | 0 |
| 0 | |
| y=c | 0 |
| y=ln[ln(x)] | |
| y=ln(x) | |
| y=li(x) | |
| y=kx+h | 1 |
| 2 | |
| y=x³ | 3 |
| y=xᵃ | a |
| y=eˣ | ℵ₀ |
| y=x!=Γ(1+x) | >ℵ₀ |
| y=xˣ | >ℵ₀ |
| ℵ₁ |
| x | y |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 1688849860263934 |
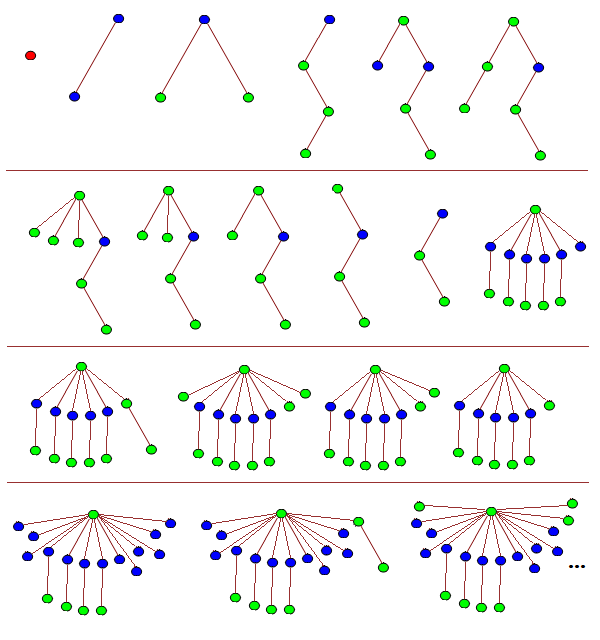
规则: 对于TREE(x), 在作树的时候, 作出的第n颗树最多有n个点, 且其分枝不得包括前边的树(不得使前边的树是这颗树的子集).
| x | y | 意味 |
|---|---|---|
| 1 | 1 | [] |
| 2 | 3 | [], (()), () |
| 3 | {}, [[]], [()()], [((()))], etc |
| T1 | {} |
|---|---|
| T2 | [[]] |
| T3 | [()()] |
| T4 | [((()))] |
| T5 | ([(())][]) |
| T6 | ([(())](())) |
| T7 | ([(())]()()()) |
| T8 | ([(())]()()) |
| T9 | ([(())]()) |
| T10 | ([(())]) |
| T11 | [(())] |
| T12 | ([()][()][()][()][()][]) |
| T13 | ([()][()][()][()][()](())) |
| T14 | ([()][()][()][()][()]()()()) |
| T15 | ([()][()][()][()][()]()()) |
| T16 | ([()][()][()][()][()]()) |
| T17 | ([()][()][()][()][()]) |
| T18 | ([()][()][()][()][][][][][][][][][]) |
| T19 | ([()][()][()][()][][][][][][][][](())) |
| T20 | ([()][()][()][()][][][][][][][][]()()()) |
| T21 | ([()][()][()][()][][][][][][][][]()()) |
| T22 | ([()][()][()][()][][][][][][][][]()) |
| T23 | ([()][()][()][()][][][][][][][][]) |
| x | y |
|---|---|
| 1 | 1 |
| 2 | 6 |
| 3 | 21 |
| 4 | 107 |
| 5 | 47176870 |
| 等级 | 种类 | 意味 | 反向 | 备注 |
|---|---|---|---|---|
| 0 | y=x | y=x | ||
| 1 | 後继 | y=x+1 | y=x−1 | |
| 2 | 加 | y=x+a | y=x−a | |
| 3 | 乘 | y=x·a=ax | y=x÷a | |
| 次幂 | xⁿ | |||
| 4 | 指数 | y=aˣ | x个a相乘 | |
| 阶乘 | y=x!=Γ(1+x) | |||
| 5 | y=a↑↑x | 暂无 | x个a连幂 | |
| a↑↑↑x | 暂无 | x个a连↑↑运算 | ||
| a↑↑↑↑x | 暂无 | x个a连↑↑↑运算 | ||
| 高德纳 | y=a↑⁽ⁿ⁾x | 暂无其明确的逆运算形式 | x个a连(n−1)个箭头的运算 | |
| y=a↑⁽ᵃ⁾(a↑⁽ᵃ⁾(a↑⁽ᵃ⁾(a↑⁽ᵃ⁾……a↑⁽ᵃ⁾(a)))=a₆(x) | 无 | a个a被a阶箭头迭代次(x−1)次 | ||
| y=a₆(a₆(a₆(a₆(……a₆(a)))))=a₇(x) | 无 | a与a被六阶运算迭代(x−1)次 | ||
| a₈(5)=a₇(a₇(a₇(a₇(a)))) | ||||
| 无 | a与a被a₇(a)阶我發明的超运算迭代了(x−1)次 | |||
| $\mathrm{y=a_{a_{a_{a_{a_{{……{a}}}}}}(a)}(a_{a_{a_{a_{a_{{……{a}}}}}}(a)}(a_{a_{a_{a_{a_{{……{a}}}}}}(a)}(a_{a_{a_{a_{a_{{……{a}}}}}}(a)}(……a_{a_{a_{a_{a_{{……{a}}}}}}(a)}(a)))))}$ | 无 | a与a被a₇(a)阶我發明的超运算迭代了很多次 | ||
| 6 | a↑⁽ˣ⁾a=ラ(a, x) |