La odometría es la estimación de la posición de un robot móvil usando para ello la información de sensores tacómetros o encoders de ruedas (ver aquí). Si añadimos información de otros sensores estaríamos hablando de "Navegación por estima" (Dead reckoning), aunque habitualmente la literatura se refiera a ambos términos como odometría.

La odometría es ampliamente utilizada en tareas de localización y navegación, dada la importancia de conocer dónde se encuentra el robot en un determinado instante de tiempo. Si un robot realiza simultáneamente tareas de localización y mapeo (generación de un mapa), estaríamos hablando de SLAM o Simultaneous Localization And Mapping (ver más).

La estimación odométrica es teóricamente sencilla, aunque pueden existir errores debido a las irregularidades del terreno que provoquen deslizamientos en las ruedas y que no se corresponda el movimiento de las mismas con la posición del robot, siendo especialmente significativos dichos errores en los giros. Por este motivo se suelen incluir sensores que estimen estos errores y los corrijan (por ejemplo giróscopos y sensores inerciales como éste).

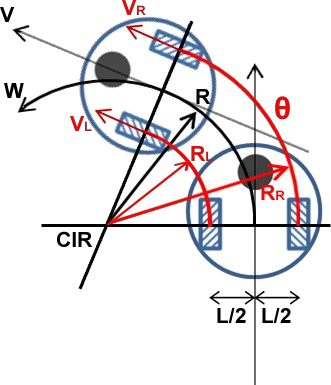
Como se ve en la imagen superior (para un robot diferencial de dos ruedas), el cálculo de la trayectoria trata de estimar la longitud recorrida por cada rueda. Con esta longitud podemos estimar el CIR-Centro Instantáneo de Rotación y conocer la trayectoria que está siguiendo el robot.

El caso de un robot diferencial de dos ruedas es relativamente sencillo (ver otras disposiciones de ruedas aquí), ya que controlamos cada rueda de forma independiente y podemos estimar fácilmente la velocidad lineal de cada una.

V_r=2π*W_r*R_wheel

V_l=2π*W_l*R_wheel

Donde:

V → Velocidad lineal del robot

V_r → Velocidad lineal rueda derecha

V_l → Velocidad lineal rueda izquierda

W → Velocidad angular del robot

W_r → Velocidad angular rueda derecha

W_l → Velocidad angular rueda izquierda

R → Radio de giro del robot

R_wheel → Radio de la rueda

L → Distancia entre ruedas

Si volvemos a comprobar la primera imagen en esta entrada:

El ángulo θ recorrido por ambas ruedas (y por el centro del robot) ha de ser el mismo en un determinado tiempo t, para ello:

θ = W / t = V_r * t / R_r = V_l * t / R_l = V * t / R

Con:

R_r = R + L/2

R_l = R - L/2

Despejando obtenemos que:

R = L/2 * (V_r+V_l) / (V_r-V_l)

y_c = y + R * cos(θ)

x_c = x + R * cos(θ)

Siendo (x,y) la posición actual del robot.

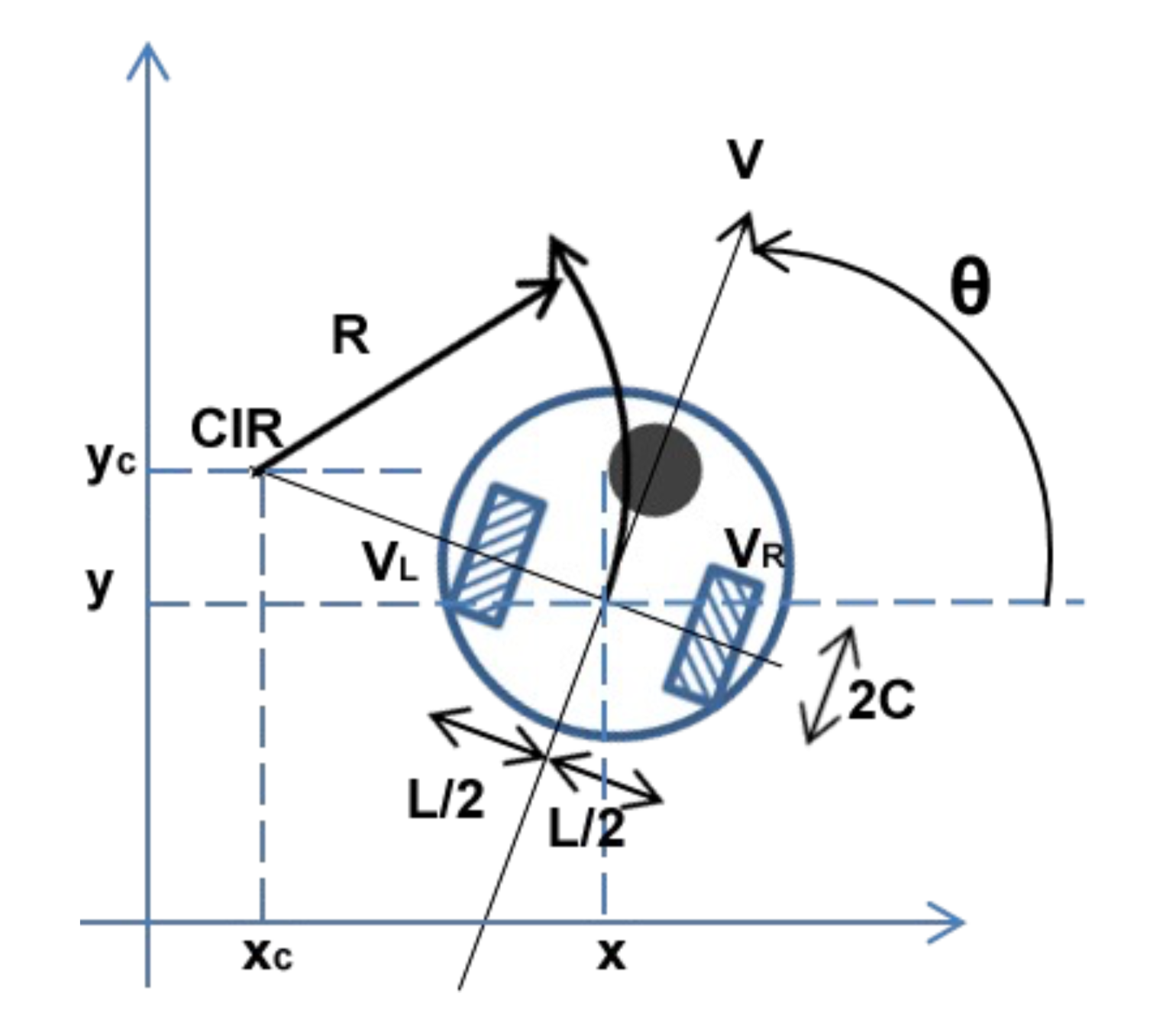
Por lo que:

• Si V_r=V_l, R → ∞ El Robot avanza/retrocede en línea recta. Esto sucede lógicamente cuando ambas ruedas avanzan en el mismo sentido (aunque el sentido de giro sea contrario cuando las miramos de frente).

• Si V_r=-V_l, R → 0 El Robot gira sobre sí mismo (realmente sobre el punto central entre las ruedas) y el CIR coincide con la posición del robot. Sucede lógicamente cuando una rueda trata de avanzar y otra de retroceder con la misma velocidad lineal.

Estas opciones suelen ser las más comunes en robótica diferencial, provocando que el robot se mueva en línea recta o gire sobre sí mismo (aunque con distintas velocidades lineales podría desplazarse en arco). Existen otras configuraciones que permiten otro tipo de movimientos (ver otras disposiciones de ruedas aquí).

Normalmente es difícil estimar las velocidades lineales del robot, por lo que se hace uso de tacómetros o encoders para estimar cuánto está avanzando cada rueda (o incluso para calibrarlas y establecer una relación software entre velocidad estimada y velocidad real).