Z OLD Homework 02 - james-bern/CS136 GitHub Wiki

https://upload.wikimedia.org/wikipedia/commons/e/e6/Conways_game_of_life_breeder_animation.gif

README (Before Lab)

swap

Imagine you want to swap the values of two variables.

This naive solution does NOT work.

int a = 0;
int b = 1;
{ // BAD VERY BAD BROKEN swap
    a = b; // a <- 1
    b = a; // b <- 1
}

The solution is to use a temporary variable.

int a = 0;
int b = 1;
{ // swap
    int tmp = a; // tmp <- 0
    a = b; // a <- 1
    b = tmp; // b <- 0
}

We can use this "swap" operation to reverse an array in-place. Note: An algorithm being "in-place" means it doesn't use any big auxiliary data structures, like, for example, a second array of length $n$.

// reverse an array of integers in-place
//
// x x x x x x x x x x 
// i ->     ^     <- j
//          |
//          array.length / 2
//
for (int i = 0; i < array.length / 2; ++i) {
    int j = (array.length - 1) - i;
    int tmp = array[i];
    array[i] = array[j];
    array[j] = tmp;
}

work array

In-place algorithms are very cool, but, sometimes it can be really convenient to use a second array. For example, when we want to update elements of array based on other elements of that array.

Here is a specific example (permuting an array according to itself):

Consider an array called array containing the integers $0, 1, 2, ..., (n - 1)$ all scrambled up.
We want to (simultaneously) replace array[i] with array[array[i]] for all $i$.
- E.g., $(3, 0, 1, 2) \to (2, 3, 0, 1)$, since for the original array
  - the $3^{rd}$ element is $2$
  - the $0^{th}$ element is $3$
  - the $1^{st}$ element is $0$
  - the $2^{nd}$ element is $1$
- Try working out what happens to $(2, 3, 0, 1)$? Did you get $(0, 1, 2, 3)$?
- Try working out what happens to $(0, 1, 2, 3)$? Did you get $(0, 1, 2, 3)$? 🤔

This naive solution does NOT work.

int[] array = { 3, 0, 1, 2 };
{ // BAD VERY BAD BROKEN update
    for (int i = 0; i < array.length; ++i) {
       array[i] = array[array[i]];
       // i = 0: array stores { 2, 0, 1, 2 }
       // i = 1: array stores { 2, 2, 1, 2 }
       // i = 2: array stores { 2, 2, 2, 2 }
       // i = 3: array stores { 2, 2, 2, 2 }
    }
}

Like the simple swap example from before, the solution is to use a temporary variable (in this case, I'll use an entire temporary array, sometimes called a "work array.")

int[] array = { 3, 0, 1, 2 };
{ // update
    int[] tmp = new int[array.length]; // tmp stores { 0, 0, 0, 0 }

    for (int i = 0; i < array.length; ++i) {
       tmp[i] = array[array[i]];
       // i = 0: tmp stores { 2, 0, 0, 0 }
       // i = 1: tmp stores { 2, 3, 0, 0 }
       // i = 2: tmp stores { 2, 3, 0, 0 }
       // i = 3: tmp stores { 2, 3, 0, 1 }
    }

    for (int i = 0; i < array.length; ++i) {
       array[i] = tmp[i];
    }
    // array stores { 2, 3, 0, 1 }

    // tmp gets garbage collected
}

Learn about how 1D Elementary Cellular Automata work.

a 1D elementary cellular automaton is a row of cells (think about little square-shaped animals living next to each other)
- in any given generation (row), a cell is either dead (0; white) or alive (1; black)
- we evolve the current generation into the next generation by applying an update rule
  - a rule tells us whether a given cell will be dead or alive in the next generation
    - it does this by considering the current state of a cell and its left and right neighbors
  - a rule is encoded as a number between 0 and 255 inclusive

Example of updating with Rule 30

By Cormullion - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=74536115

By Cormullion - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=74536115

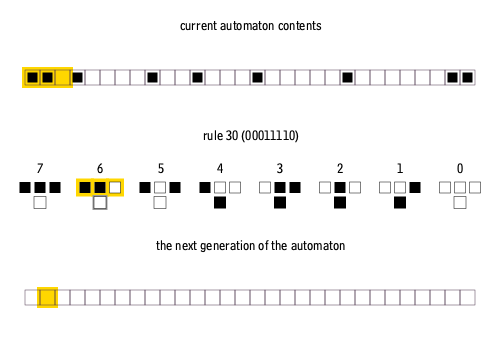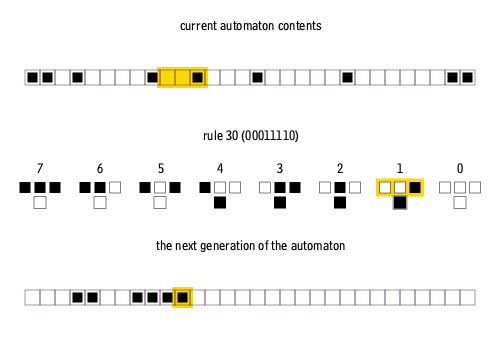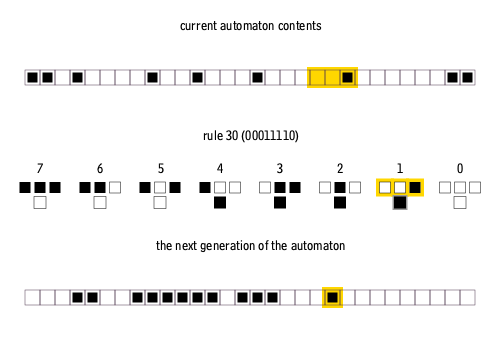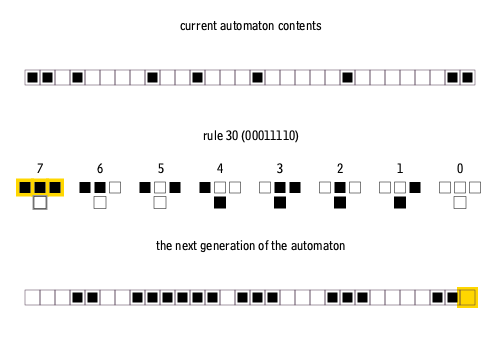
Let's look at the update of just the 1st cell; here is the situation:

The state of "the three cells neighboring [the first cell]" is $110$
- The 1st cell's left neighbor (the 0th cell) is currently alive ($1$).
- The 1st cell is currently alive ($1$).
- The 1st cell's right neighbor (the 2nd cell) is currently dead ($0$).

...110...   // current generation
    |
 Rule 30
    |
    v
    ?       // next generation

Interpreted as a $3$-digit binary number, the state of "the three cells neighboring [the first cell]" is $110_2 = (1 * 4) + (1 * 2) + (0 * 1) = 6.$ (The subscript $2$ in $110_2$ just means "this number is written in binary".)

In this example, we're applying Rule 30.

Written as $8$-digit binary number, $30 = 00011110_2$.

To find out what happens to the 1st cell, we read out the $6$-th digit of the 8-digit binary representation of the rule $00011110_2$

(🚨 Note: Like in the last homework, we index into the digits of this binary number from right-to-left)

 |
 v
00011110 binaryRepresentationOfRule

The 6th digit happens to be $0,$ meaning that the 1st cell will be dead in the next generation. ☹️

...110...   // current generation
    |
 Rule 30
    |
    v
    0       // next generation

Note: The approach described above works for any rule. However, if we just want to implement a single rule, for example Rule 22, we can sometimes take a shortcut.

Additional Reading

Read the first two paragraphs of this Wikipedia article
Read (skim) the Wolfram MathWorld article on ElementaryCellularAutomaton.
Try simulating Rule 22 on paper.
array Documentation

Specification

To get a B:
- ✅ Simulate just Rule 22.
  - ✅ To store the automaton's state, create a new array of 79int's.
    - ✅ Set the middlemost element to '1'; leave all the others elements be '0'.
      - 🚨 There should NOT be a 39 in your code. Use array.length / 2.
  - ✅ For 32 generations...
    - ✅ Print each generation (row) of the automaton using exactly one call to System.out.println (you will call System.out.println 32 times as you simulate the automaton, once for each generation/row).
      - ✅ Print as shown below, where live cells are marked with an 'X' and dead cells are marked with a ' '.
      - ✨ You will need to build up a String. I recommend just using the + operator for String's, though Java also has something called StringBuilder which you are welcome to use.
    - ✅ Update the automaton according to Rule 22 (step one generation into the future)
      - ✨ I chose Rule 22 for this homework because it is easy code up. :) You should need very little code to check it for a given cell. Here is a hint for a shortcut for Rule 22.
        
        ✨ Here is a hint for the hint: +
      - 🚨 You will need to decide how to update the cells with index 0 (far left) and index array.length - 1 (far right); they are special! (The far left cell has no left neighbor; the far right cell has no right neighbor.) What should we do? ✨ I recommend not updating these cells at all; just leave them zero. Problem solved. 🙂👍
  - 🚨 I recommend NOT writing any additional functions for this homework. If you really feel like you absolutely need a function, you can use one. 🙂👍
  - 👀 Given our starting state (just one live cell in the middle), the first 16 generations of Rule 22 must look something like this:
```
                                       X                                       
                                      XXX                                      
                                     X   X                                     
                                    XXX XXX                                    
                                   X       X                                   
                                  XXX     XXX                                  
                                 X   X   X   X                                 
                                XXX XXX XXX XXX                                
                               X               X                               
                              XXX             XXX                              
                             X   X           X   X                             
                            XXX XXX         XXX XXX                            
                           X       X       X       X                           
                          XXX     XXX     XXX     XXX                          
                         X   X   X   X   X   X   X   X                         
                        XXX XXX XXX XXX XXX XXX XXX XXX                              
```
To get an A:
- ✅ Extend simulate1DAutomaton to simulate whatever rule is passed to the funtion. Carefully check your output against the pictures from the reading.
  - 👀 The outputs of Rules 0-4 match images from https://mathworld.wolfram.com/ElementaryCellularAutomaton.html
    - Because of how we handle the boundaries, some of the other pictures may not match. Do no fret. Just check 0-4 and 22 visually.
  - ✨ The README is your friend.
  - 🚨 Do NOT use String's to do anything besides print the automaton. (I.e., do NOT call getInBinary from the last homework and then do a bunch of conversions.)
  - 🚨 To score points, you final submission should NOT use a giant chained if-else of the form if (... == 0) { ... } else if (... == 1) ... else if (... == 6) { ... } else { ... } 🙅‍♂️ Instead, use binary numbers to your advantage :)
  - ✨ There are many approaches to this problem, but I recommend using an array. The sample solution builds an array of 8 ints at the very top of simulate1DAutomatoncalledint[] binaryRepresentationOfRuleRightToLeft = new int[8];` To index into the binary number later, you can just index into this array! Wow! :D
To get an S:
- Implement Conway's Game of Life in 2D.
  - ✨ See the Snippets sections of our Documentation for a function called sleepThenClearTerminal.
  - ✨ See our Lecture Slides for a short explanation of multi-dimensional arrays.

Submission Instructions

Upload your code file to GradeScope by the due date.
Live demo your code to Jim or a Grading TA in Lab.
- 🚨 You must do this in order to receive points.
- If you are trying for an S, you must demo to Jim.

Starter Code

import java.util.*;

class HW02 {
    static void simulate1DAutomaton(int rule) {
        assert (rule >= 0) && (rule < 256);
        // TODO
    }

    public static void main(String[] arguments) {
        simulate1DAutomaton(22);

        // for (int rule = 0; rule < 5; ++rule) {
        //     System.out.println("\n----------------------------------- RULE " + rule + " -----------------------------------\n");
        //     simulate1DAutomaton(rule);
        // }
    }
}