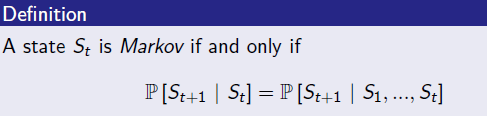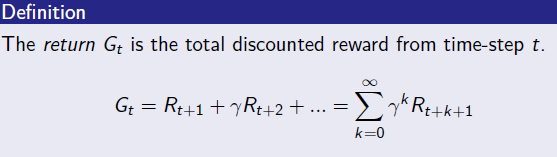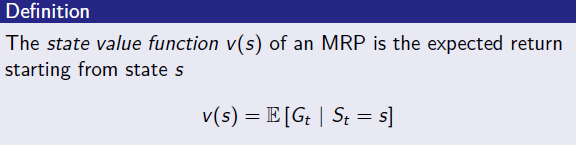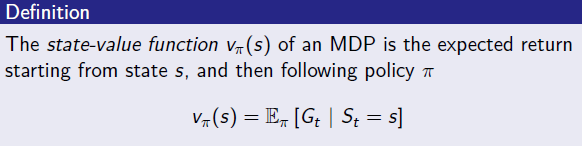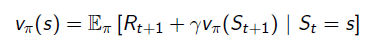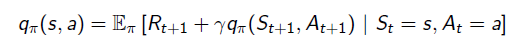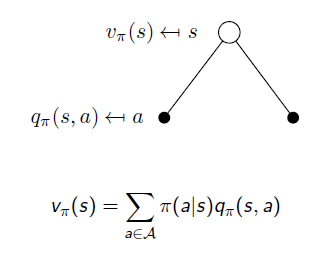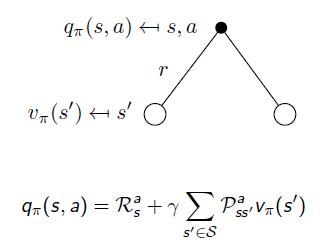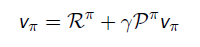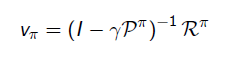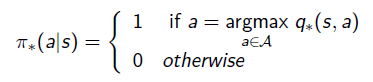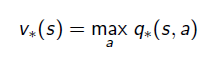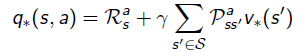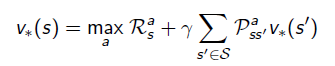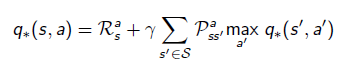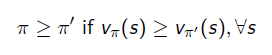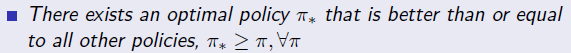학습의 분류

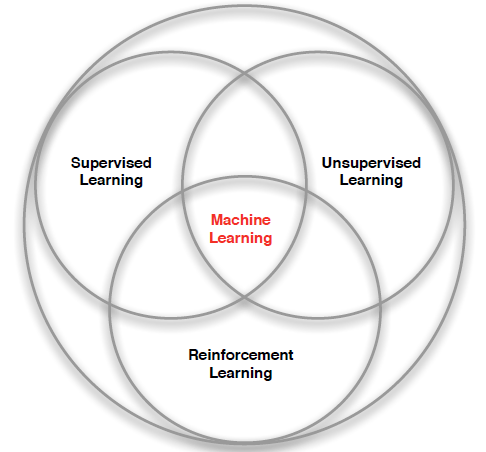
• Machine Learning (기계학습)
  • 기계에 무언가를 배우게 하는 것
• Supervised Learning(지도학습)
  • 훈련 데이터(Training Data)로부터 하나의 함수를 유추해내기 위한 기계 학습의 한 방법
    • 하나의 함수를 유추해내기 위해 정답지(Label)가 존재해야 함.
    • 함수의 유효성을 검증하기 위해 테스트 데이터(Test Data)가 존재하는 것이 관습적.
  • 훈련 데이터는 Raw Input이 될 수도 있고 Raw Input을 가공한 데이터 -> Feature 데이터로 구성할 수도 있음
  • 신경망 학습(or 딥러닝)과 기존의 통계적 머신러닝(Logistic, Decision Tree, Random Forest, SVM etc)의 본질적인 차이는 Layer를 쌓아서 다층적 구조를 만들어 더 동적인 패턴을 발견할 수 있느냐 여부
    • 하지만 일반적으로는 Raw Input만으로도 feature를 자동으로 추출하는 학습 방식이라고도 말하나 이는 엄밀히는 설계의 차이에 가까움
• Unsupervised Learning(비지도학습)
  • 훈련 데이터까진 지도학습과 동일하나 정답지(Label)이 없이 학습하는 방법론
  • 주로, 데이터가 어떻게 구성되어 있는 지(특징,구조)에 관한 문제를 품
    • ex) 클러스터링, PCA
• Reinforcement Learning(강화학습)
  • 순차적 의사결정 문제에서 누적보상을 최대화 하기 위해 시행착오를 통해 행동을 교정하는 학습 과정
    • 순차적 의사결정 문제를 푸는 것을 전제로 하기 때문에 '퀀트'와도 잘 맞는다.
    • 특히, 전제가 순차적 의사결정이기 때문에 non iid여도 상관없다. ML은 iid여야 하기 때문에 다음과 같은 복잡한 절차가 필요 DataStructures

강화학습의 구조

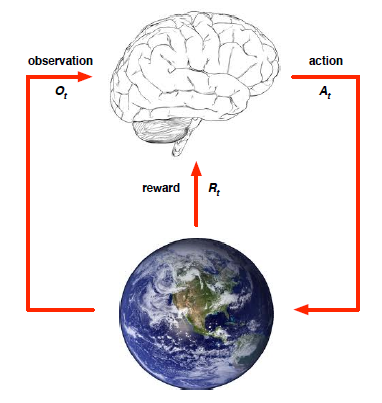
• Architecture
  • Agent : 강화학습의 주체
  • Environment : Agent를 제외한 모든 요소
  • Flow : Agent는 action을 하고 action에 대한 반응을 Environment에서 제공함. State & Reward를 Agent는 응답 받음. 해당 Loop를 일정 주기(time step)로 반복함. 이런 trial & error를 반복하여 정답지(Label, 어떻게)가 없이 최적의 action을 할 수 있는 Agent가 될 때까지 반복.
    • Reward 개념과 지도학습의 Label 데이터 개념은 구별됨.
• vs 지도학습
  • 보상(Reward) 개념 자체가 sparse(희소) & delay(지연) 될 수 있다는 것 자체에서 지도학습의 Label 데이터를 통한 학습과 본질적으로 다르게 만듦.
    • 지도학습에선 훈련데이터와 Label 데이터 간의 관계를 '직접 & 바로' 함수로 표현하기 때문
    • 강화학습에선 action에 시간의 흐름에 따른 고려 자체도 학습의 대상 안에 들어간다고 볼 수 있음
  • Quant 관점
    • 1. 지도학습을 통해 여러 전처리 작업(for iid)을 하는 과정과 리서치를 통한 feature 생성하는 Factory를 만드는 퀀트 시스템
    • 2. 강화학습을 통해 feature(사전지식) 없이 철저한 trial & error를 통한 다수의 agent를 보유한 퀀트 시스템
    • 무조건 한쪽이 좋다고 말할 수 없고 서로가 구조적으로 다르기에 다른 패턴을 찾아낼 가능성은 높다고 보기 때문에 퀀트 시스템 자체도 Ensemble하여야 함.

MDP (Markov Decision Process)

MP (Markov Process)

• MP = (S,P)이고 initial state -> terminal state 까지의 Process에서 P(transition prob matrix)의 원소 P(transition prob)에 의해서 state 간 이동이 결정된다.

Markov Property

• 
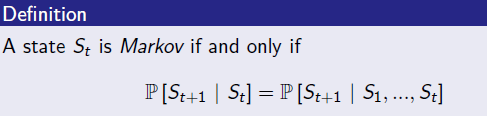
  • "미래는 오로지 현재 상태에 의해 결정된다"는 대전제에 의해 MP가 정의된다.
  • 다만, Markov Property는 두 가지 방향으로 확장될 수 있다. 확장을 통해 다양한 variant version이 탄생할 수 있다.
    • t시점과 t+1시점의 정보가 꼭 State일 필요는 없다. (Reward, Action으로도 확장 가능 > MRP,MDP)
    • 꼭 t+1과 t시점간의 관계일 필요가 없다. (t+1 <- (t,t-1,t-2))

MRP (Markov Reward Process)

• 
• 
• 
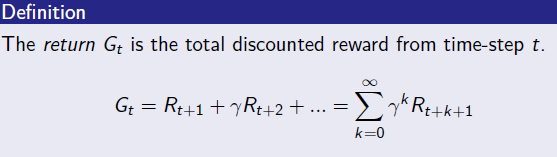
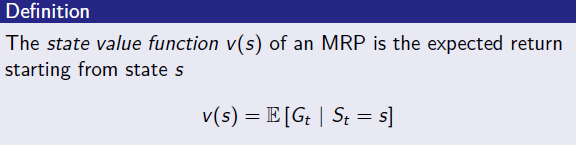
  • MRP = (S,P,R,gamma) 이고 S,P의 정의는 MP와 동일
  • **R(Reward Function)**은 어떤 상태 S_t에 도달했을 때 받는 보상을 의미하고 어떤 상태냐에 따라 달라지는 random variable이기에 Expectation을 활용해 표현됨.
  • gamma 는 decay factor이고 0~1의 값을 가진다.
    • why? 1) 발산을 방지하는 수학적 편리성, 2) 시간 선호 모델링, 3) 미래 가치에 불확실성 투여
  • 강화학습 프로세스를 episode라고 부르며 이는 s0, R0, s1, R1 ... sT, RT 까지의 여정을 의미한다. 이때 임의의 시점 T에서 앞으로 받는 보상의 합은 의미적으로 중요하기에 수학적으로 다음과 같이 표현한다. Return G_t로 정의하고 수식으로 t+1~N시점 까지의 sum of gamma*reward라고 말할 수 있다.
  • T시점에서의 상태가 갖는 가치(value)를 어떻게 정량화 할 것인가? 정량화된 형태를 **상태가치함수(state-value function)**로 정의하고 이는 St=s일 때의 Return의 기댓값으로 표현한다. s부터 어떤 sampling을 하여 어떤 episode가 구성되느냐에 따라 return의 값이 달라지기 때문에.

MDP (Markov Decision Process)

• 
• 
• 
• 
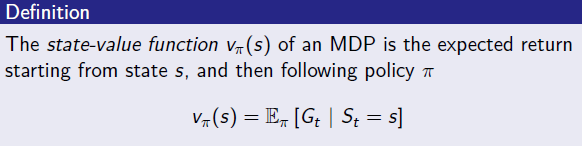
  • MDP = (S,A,P,R,gamma) MRP에 decision 개념 (by action, policy)이 추가되었음.
  • 이전엔 s->s'의 이동이 transition state probability에 의해서만 state가 변했다면 action을 통해서 state가 변하는 것에 영향을 주는 확률적 과정이 하나 더 추가됨
  • policy function(pi function)는 각 상태 s에 따라 어떤 action a를 선택할 확률을 의미함
  • MDP하에서의 state-value function은 s->s' transition 할 때 pi에 따라 움직인다는 점을 제외하고는 수식적으론 동일하다.
  • (state-)action value function은 '각 상태에서의 액션을 평가'하기 위함. 이때 action만 따로 평가는 불가능함.
    • V_pi_(s)는 s에서 pi가 액션을 선택하고 q_pi_(s,a)는 s에서 강제로 a를 선택한 상태를 의미한다. 일종의 A_t=a 조건부 상태.

For What

• Prediction : pi가 주어졌을 때 각 상태의 value를 평가하는 문제
• Control : 최적 정책 pi_star를 찾는 문제

Bellman Equation (MDP)

Bellman Expectation Equation

• 
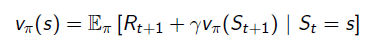
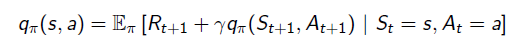
  • G_t의 정의에 따라 재귀적으로 표현하면 위의 수식이 도출됨.

---

• 
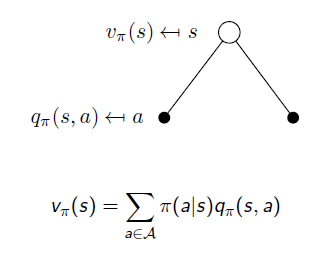
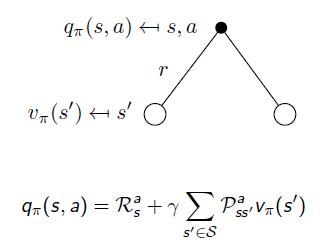
• 위의 수식은 현재 상태와 다음 상태 value를 expectation을 통해서 연결한 식인 반면 위의 식은 실제 계산하는 과정을 수식화
• v_pi_(s) [s의 value]를 1-time-step에서 action a를 실행하기 전을 분해해보면 s에서 a를 실행할 확률과 s에서 a를 실행하는 것의 value의 곱으로 표현된다. 그리고 모든 time-step에 적용하기 위해 집합 A에 대해 sum
• q_pi_(s) [s에서 a를 실행하는 것의 value]는 action a를 통해서 얻는 보상과 s에서 a를 통해 s'갈 확률과 s'의 value를 곱한 것을 이후 모든 상태에 적용한 sum으로 표현할 수 있다.

---

• 
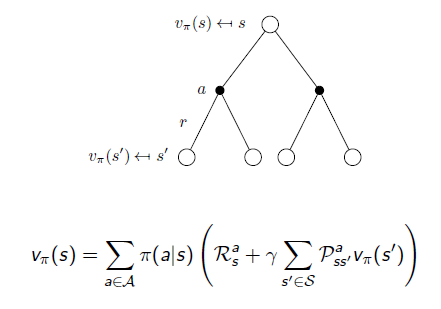
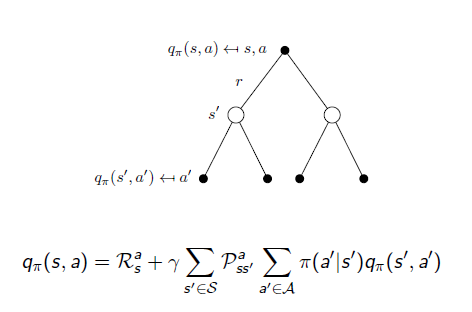
  • 위의 수식을 통해 서로 교차하여 대입하면 다음과 같이 유도된다.
  • 위의 식으로 통해 r_s, P_ss'를 알면 직접적으로 계산할 수 있음을 보여준다.

---

• 
  • matrix form으로 표현한 수식

---

Bellman Optimal Equation

• 
  • 다른 정책을 따를 때 보다 optimal policy pi star를 따를 때 얻는 보상의 총 합이 가장 크다는 것을 의미한다.
  • optimal policy에 관련해서는 partial ordering의 개념으로 생각해야 함.
    • 
  • 여기에 더해 다음과 같은 정리가 증명되어 있으므로 optimal policy를 찾는 것을 증명하는 것에 전념할 수 있음.
    • 

---

• 
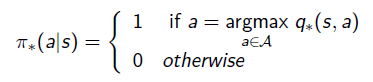
  • policy function은 optimal한 것으로 정해졌기에 deterministic 해짐.

---

• 
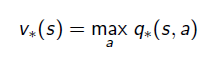
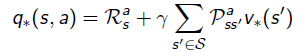
  • Bellman Expectation Equation의 pi를 위의 1 값으로 고정되면서 위와 같은 식이 유도됨. q입장에선 달라지는 것은 없음. 이미 a가 결정된 상태에서의 식이기 때문에.

---

• 
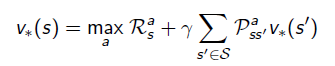
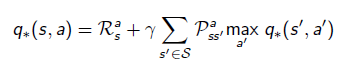
  • v_(s)는 식 전체에 max a를 취한다. 식 전체가 a와 dependecy가 있기 때문에. q_(s,a)의 경우는 action a와 관련한 것은 이미 결정된 것들이고 다음 스텝에서의 action a'에 관해서만 max a를 취한다.

For What

• Bellman Expectation Equation은 정책 pi가 주어져 있고 pi를 평하고 싶을 때 사용하고, Bellman Optimal Equation은 최적의 value를 찾고 싶을 때 사용함
• MDP 문제
  • model-free :r^a_s와 P^a_ss`를 모르는 경우 experience를 통해 해결
  • model-based : r^a_s와 P^a_ss`를 모두 아는 경우

Model-Based (Planning)

Model-Free Prediction

Model-Free Control

Basic of Deep RL

DAVID SILVER, UCL Course on RL