Matrix Calculus - jaeaehkim/trading_system_beta GitHub Wiki
Motivation
- 스칼라 입력을 받고 스칼라 출력을 하는 함수 >> 벡터/행렬 입력으로 받아서 벡터/행렬 출력하는 함수로 확장
- 더 다양한 문제를 함수로 모델링 할 수 있음
- 행렬을 입출력을 미분하는 것을 matrix differentiation이라 하고 편미분의 확장하는 개념
- 표현 방식이 1)분자중심 표현법(Numerator-layout notation), 2)분모중심 표현법(Denominator-layout notation)이 있고, 많은 페이퍼에서 한 가지 방식으로 서술하나 일부 페이퍼는 혼용하는 경우가 있기 때문에 정확히 읽는 습관을 갖는 것이 중요
Input/Output Case
vector -> scalar
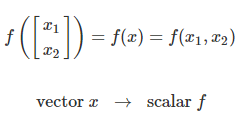
matrix -> scalar
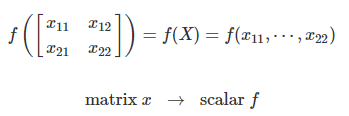
scalar -> vector
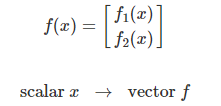
scalar -> matrix
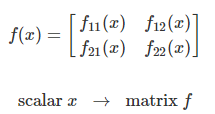
vector -> vector
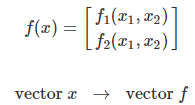
vector -> matrix

scalar를 vector로 미분하는 경우 (입력 : vector -> 출력 : scalar)
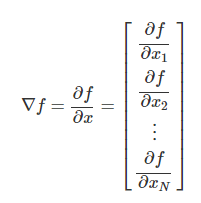
- delta f 를 gradient vector라고 부른다.
- 데이터 분석에선 입력을 벡터로 받고 출력을 스칼라로 하는 경우가 많음.
행렬미분 공식1 : 선형모형
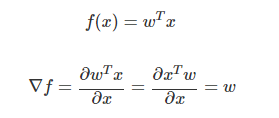
- w, x 는 모두 vector
행렬미분 공식2 : 이차형식
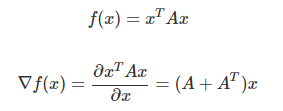
- x는 vector, A는 matrix
vector를 scalr로 미분하는 경우 (입력 : scalar -> 출력 : vector)
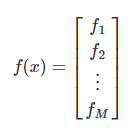
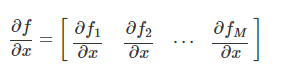
vector를 vector로 미분하는 경우 (입력 : vector -> 출력 : vector)
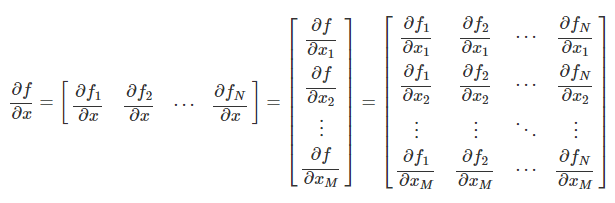
행렬미분 공식3 : 행렬과 벡터의 곱의 미분
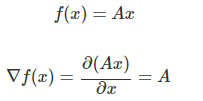
- 행렬A와 벡터x
자코비안 행렬 (Jacobian Matrix)

- 함수의 입출력 모두 다차원인 경우 도함수를 구하면 행렬 형태를 갖게 된다.
- 자코비안 행렬은 벡터 함수를 벡터 변수로 미분해서 생기는 행렬의 전치행렬 (도함수 행렬)
헤시안 행렬 (Hessian Matrix)
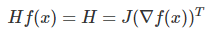
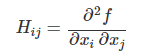
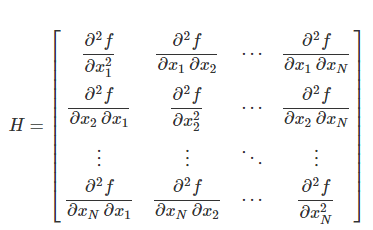
- gradient vector를 입력 변수 vector로 미분한 것이고 다변수 함수의 2차 도함수
scalar를 matrix로 미분하는 경우 (입력 : matrix -> 출력 : scalar)
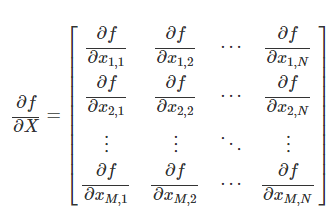
행렬미분 공식4 : 행렬 곱의 대각성분
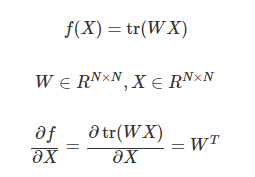
행렬미분 공식5 : 행렬식의 로그
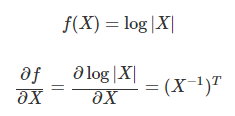
Summary

- a,b : 상수 벡터
- A : 상수 행렬
- y,z : x와 함수관계 갖는 벡터