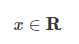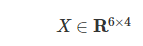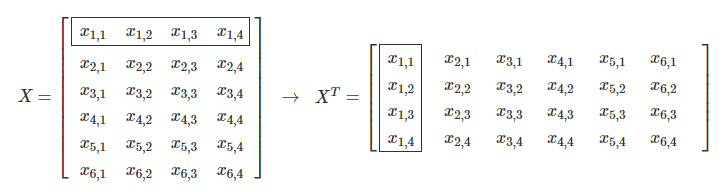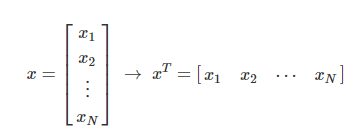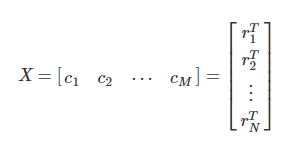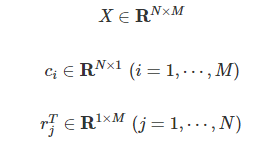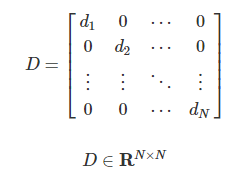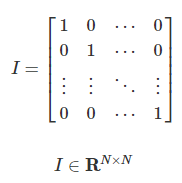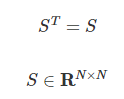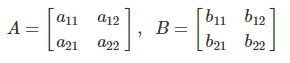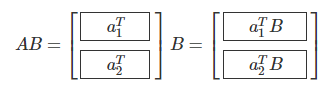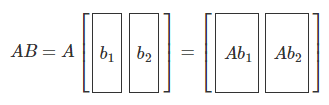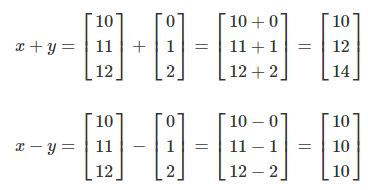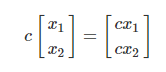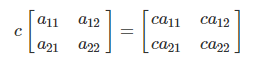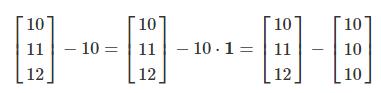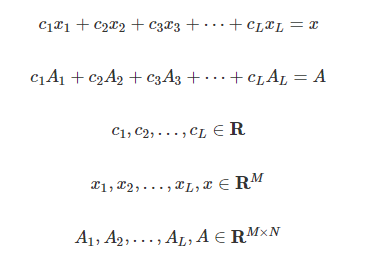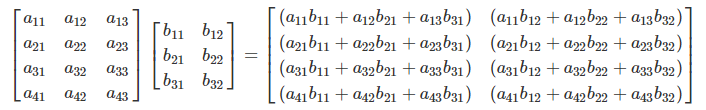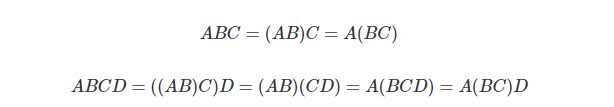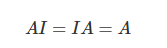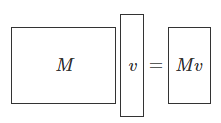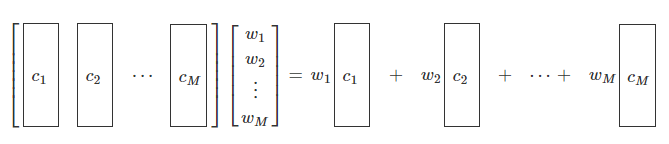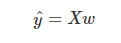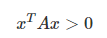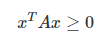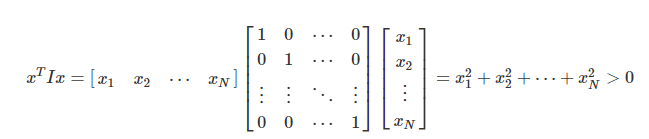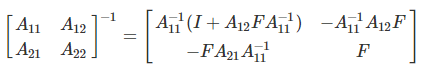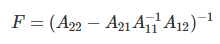Linear Algebra Basic - jaeaehkim/trading_system_beta GitHub Wiki
-
스칼라(scalar) : 숫자 하나로 이루어진 data
-
벡터(vector) : 여러 숫자로 이루어진 data record
-
-
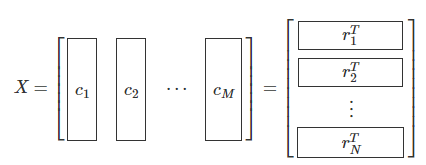
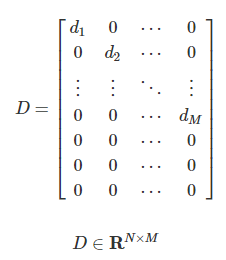
행렬(matrix) : vector가 여럿인 data collection
-
-
텐서(tensor) : 같은 크기의 행렬이 여러 개 있는 것 (768 x 1024 x 3)
- 열 개수 == 행 개수
- 요소별(element-wise) 연산
-
- 1-vector를 활용해 스칼라를 벡터로 변환한 연산을 자동으로 수행하는 것
- 벡터/행렬에 스칼라 값을 곱한 후 더하거나 뺀 것을 의미. 선형조합을 해도 크기는 변하지 않음.
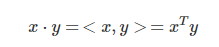
-
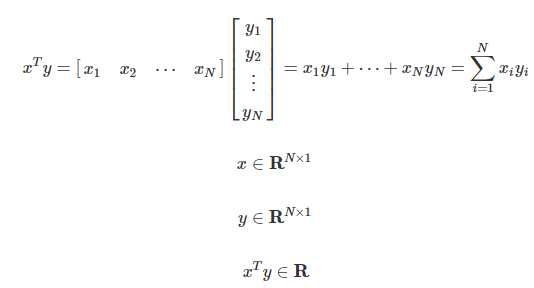
- 조건 1 : 벡터의 차원(길이)이 동일해야 함.
- 조건 2 : 벡터가 전자는 행 벡터, 후자는 열 벡터여야 함.
-

-
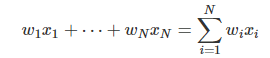
- w = weight vector , x = data vector
-
-
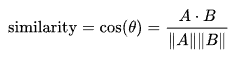
- A,B vector
-
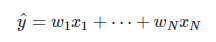
-
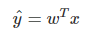
- 독립변수 x에서 종속변수 y를 '설명' or '예측'할 때 사용함 y hat은 예측 또는 추정 값이 된다.
- 어떤 독립변수를 쓰느냐에 따라 설명,예측 퍼포먼스가 달라지고 선형 결합만으로 설명해야 한다는 단점이 존재한다.
-
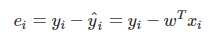
-
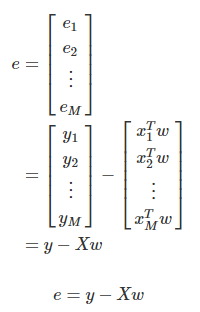
- 예측치와 실젯값(target)의 차이를 오차(error) 또는 잔차(residual)이라고 부른다.
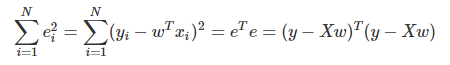
-
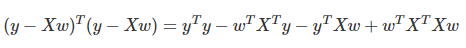
- 잔차 벡터의 제곱 합을 간단하게 표현 가능하며, 분배법칙을 활용해 풀어쓰는 것도 가능하다.
-
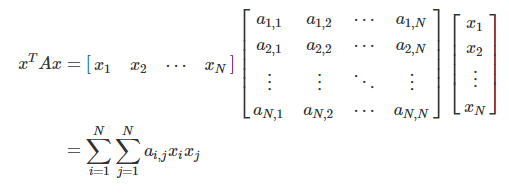
- "행벡터 X 정방행렬 X 열벡터"의 형식으로 되어 있음
- 정부호
- 준정부호
- Example
-
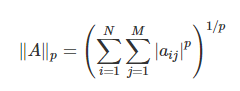
- 행렬의 norm에 다양한 정의가 있지만 entrywise matrix norm로 정의한다. p=2가 일반적인 경우
- Case : p==2:
-
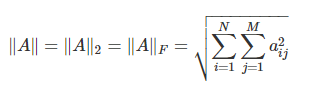
- norm은 항상 0보다 크거나 같다.
-
-
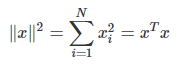
- 벡터의 norm은 벡터의 제곱합과 같다.
- 벡터의 norm을 최고화 하는 것은 벡터의 제곱합을 최소화 하는 것과 같다.
-
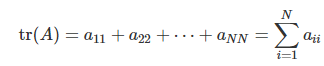
- 대각합은 정방행렬에서만 정의되며 대각 원소의 합으로 계산된다.
- 성질
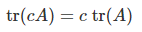
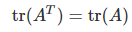
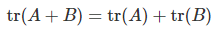
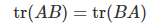
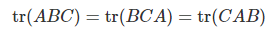
-
Trace Trick
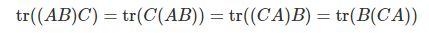
-
Quadratic Form :
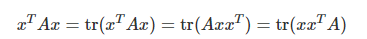
- 행렬 A가 스칼라(1X1)인 경우의 행렬식은 자기 자신의 값이 된다.
- 행렬 A가 스칼라가 아닌 경우 : 여인수 전개(cofactor expansion)
-
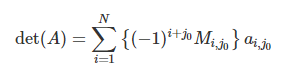
-
Cofactor :
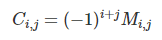
-
Cofactor :
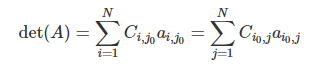
-
-
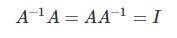
- 위의 식을 만족하는 정방행렬 A는 inverse of A가 존재한다.
- 역행렬이 존재하는 행렬을 가역행렬(invertible matrix), 정칙행렬(regular matrix), **비특이행렬(non-singular matrix)**라고 부른다.
- 역행렬이 존재하지 않는 행렬을 비가역행렬(non-invertible matrix), 특이행렬(singular matrix), **퇴화행렬(degenerate matrix)**라고 부른다
-
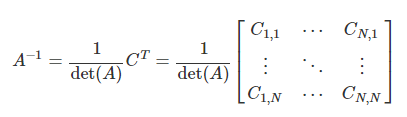
- 행렬 C는 여인수 행렬(matrix of cofactors)라고 부르며, 전치행렬 C(T) (adjoint matrix)라고 부르며 adj(A)라고 표기하기도 한다.
- det(A) != 0일 때만 역행렬이 존재한다.
- 셔먼-모리슨(Sherman-Morrison) 공식
-
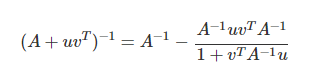
- 정방행렬 A, 벡터 u,v
-
- 우드베리(Woodbury) 공식
-
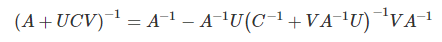
- 정방행렬 A, 적절한 크기 행렬의 U,V,C
-
- 분할 행렬의 역행렬
-
-
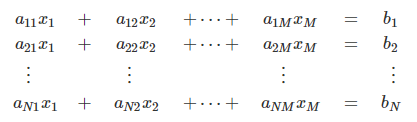
- x : M개의 미지수, N개의 선형 연립방정식, a,b는 방정식의 계수
-

- 행렬의 곱과 벡터를 활용해 표현
-
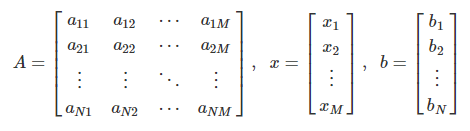
-
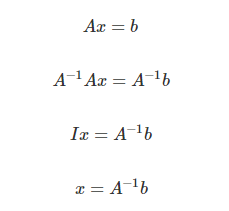
- 행렬 A의 역행렬이 존재한다는 가정 하에서 위와 같이 구할 수 있음.
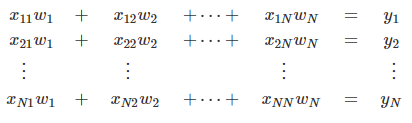
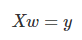
-
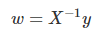
- 선형 예측 모형의 가중치 벡터를 구하는 문제를 푸는 경우에 Train Data x와 label y를 알고 있을 때 weight vector를 구할 수 있다.
- weight vector를 아는 상태에선 Feature X가 주어진다면 y를 예측할 수 있다.
-
미지수의 수와 방정식의 수 Issue
- 미지수의 수(N) == 방정식의 수(M)
- 위에서 다룬 것과 동일
- 미지수의 수(N) > 방정식의 수(M)
- 방정식 M개를 만족하는 해가 무한히 많다.
- 미지수의 수(N) < 방정식의 수(M)
- 방정식 M개를 모두 만족하는 해는 존재하지 않는다.
- 미지수의 수(N) == 방정식의 수(M)
- 해가 존재하지 않는 경우에 선형 예측 모형은 답을 어떻게 구할까?
- 정확한 값을 구하는 것이 아닌 근사 값을 구하자
- 정확한 값을 구하다 보니 만족하는 방정식과 만족하지 않는 방정식이 나오게 된다.
- 모든 방정식의 좌변과 우변의 차이를 최소화하는 문제로 변형 : error vector의 norm을 최소화
- 정확한 값을 구하는 것이 아닌 근사 값을 구하자
- Solution
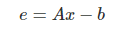
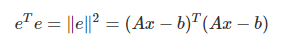
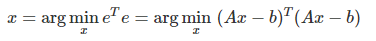
- Flow
-
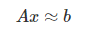
- 같다고 가정 후 계산
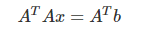
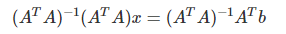
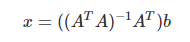
-
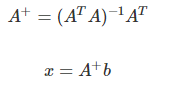
- 디테일한 부분은 행렬의 미분과 최적화를 활용
-