Binary Tree atau Binary Search Tree atau bisa disingkat Tree adalah salah satu struktur data yang fundamental dan lumrah digunakan di dalam ilmu komputer. Berbeda dengan linked list, array, stack, dan queue, Tree secarad esain memiliki desain yang tidak linear (tidak berbaris atau berurut). Tree sendiri merepresentasikan struktur yang hierarki, dimana elemen-elemen tersusun dalam beberapa tingkatan. Hal ini menjadikan urutan informasi pada Tree dapat diabaikan.

Sebuah tree terdiri dari node dan 2 pointer, dua pointer ini sendiri merupakan child kiri dan child kanan dari node induk atau parent node. Untuk memudahkan pembelajaran pada materi ini, perlu dibaca dan dipahami beberapa istilah teknis yang tidak mungkin diterjemahkan ke bahasa indonesia secara baik dan relevan.

• Root

Root dari tree adalah node paling atas dari sebuah tree yang tidak memiliki parent node. Dalam satu buah sistem tree, hanya ada satu buah root

• Parent Node

Parent Node adalah pendahulu dari sebuah node

• Child Node

Child Node dapat diartikan sebagai cabang, atau peranakan, atau pewaris dari sebuah node

• Sibling

Sibling merupakan child node yang berasal dari parent node yang sama

• Edge

Edge adalah sebuah garis yang menghubungkan antara node

• Leaf

Leaf merupakan sebuah node yang tidak memiliki child node dan berada pada bagian paling bawah dari sebuah sistem tree. Leaf merupakan node terakhir dari sistem tree dan sebuah tree dapat memiliki leaf lebih dari satu

• Subtree

Subtree adalah sebuah sistem tree dimana satu parent node dipatok menjadi root di sistem tree yang sama

• Depth

Depth ialah jarak dari root ke sebuah node

• Height

Height adalah jarak yang ditempuh dari satu node ke Leaf (node paling bawah) pada sebuah tree

• Height of tree

Height of tree merupakan jarak maksimal yang ditempuh oleh node apapun. Nilai dari height of tree merupakan jarak dari root ke leaf

• Level

Level atau tingkatan adalah besaran kedalaman dari sebuah tree yang dihitung berdasarkan banyaknya barisan parent node yang ada secara vertikal

• Degree of node

Degree of node merupakan banyaknya children yang dimiliki

Berikut adalah diagram untuk memvisualisasikan sebuah keadaan tree yang melibatkan istilah di atas:

1. Full Tree

Full tree terjadi apabila sebuah node hanya memiliki 2 atau 0 child node, atau yang berarti seluruh parent node di tree tersebut memiliki child node yang lengkap, yaitu 2 buah, kecuali leaf node. Apabila L merupakan jumlah leaf node dan l merupakan jumlah node selain leaf node, didapatkan L = l+1

2. Complete Tree

Complete tree terjadi dimana seluruh level terisi kecuali level terakhir, seperti yang digambarkan di atas

3. Perfect Tree

Perfect tree merupakan tree yang terdiri dari seluruh node memiliki dua children node dan seluruh leaf node berada dalam level yang sama. Perfect tree yang memiliki height h memiliki banyak node sebesar 2^h-1

4. Degenerate Tree

Degenerate tree adalah tree yang dalam keadaan seluruh parnet node hanya memiliki satu child. Apabila dilihat dari cara kerja dan performa, dapat dikatakan bahwa degenerate tree adalah sebuah linked list

5. Balanced Tree

Balanced tree adalah tree yang depth dari dua buah subtree di node yang sama, memiliki perbedaan level yang tidak lebih dari 1.

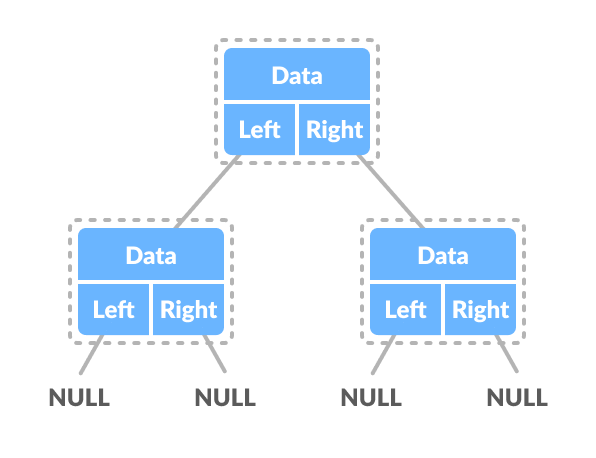
Representasi dasar dari sebuah tree pada kode C++ dapat dilihat melalui kode dan diagram berikut ini

struct node
{
 int data;
 struct node *left;
 struct node *right;
};

Pada dasarnya, tree pada umumnya direpresentasikan sebagai pohon yang terbalik. Tree dimulai dari root, yang berisi key value asli. Root memiliki dua child node, yang setiap child node juga bisa memiliki masing-masing child node sendiri. Struktur ideal dari tree ini adalah sebuah tree yang seimbang, dimana child node dari root memiliki banyak child node yang sama, baik child kiri dengan child kanan. Tree yang seimbang memungkinkan untuk data yang dimasukkan maupun yang diambil dari tree diproses dengan cepat.

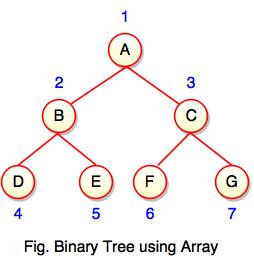
Apabila dibentuk menjadi array, setiap node akan diurutkan berdasarkan level dan posisi node. Node diurutkan dari atas kebawah, dan mendahulukan dari kiri ke kanan. Setiap ruang kosong pada level tersebut juga dihitung.

Operasi-operasi sederhana yang dapat dilakukan di tree diantaranya adalah sebagai berikut:

1. Insertion

2. Search

3. Traversal, yang akan terbagi menjadi tiga metode

4. Insertion

Operasi insertion atau memasukkan data ke dalam tree, dilakukan dengan mencari terlebih dahulu tempat data ditaruh. Algoritma dimulai dari root. Apabila elemen yang akan dimasukkan lebih kecil dari key value, maka arahkan ke subtree sebelah kiri. Selain itu, arahkan ke subtree sebelah kanan. Lakukan hingga selesai (tidak ada elemen yang perlu dikomparasi lagi) dan masukkan data.

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty, create root node
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent  = NULL;

      while(1) {                
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }
			
         //go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

2. Search

Algoritmanya mirip dengan memasukkan elemen ke tree. Apabila data yang dicari lebih kecil dari key value, maka lakukan pencarian ke subtree kiri, selain itu, lakukan pencarian ke subtree kanan. Setelah menemukan elemen yang cocok, lakukan return data. Apabila seluruh tree sudah dicari dan elemen tidak ditemukan, maka lakukan return NULL.

struct node* search(int data) {
   struct node *current = root;
   printf("Visiting elements: ");

   while(current->data != data) {
      if(current != NULL)
      printf("%d ",current->data); 
      
      //go to left tree

      if(current->data > data) {
         current = current->leftChild;
      }
      //else go to right tree
      else {                
         current = current->rightChild;
      }

      //not found
      if(current == NULL) {
         return NULL;
      }
   }
   return current;
}

3. Traversal

Traversal dalam hal ini adalah algoritma sebuah program untuk melakukan pencarian terhadap suatu elemen. Pada tree, bentuk traversal ini ada berbagai macam cara dikarenakan struktur dari tree sendiri yang tidak berbaris maupun tidak terurut, sehingga muncul berbagai pemahaman tentang bagaimana cara mencari suatu elemen pada tree. Ada tiga macam bentuk algoritma yang dapat diterapkan, yaitu:

• Preorder Traversal

Algoritma ini dimulai dengan node awal atau node saat ini (root), lalu bergerak ke arah kiri dari child, hingga ke kanan dari child. Outputnya berupa root -> seluruh child di kiri -> seluruh child di kanan

• Inorder Traversal

Algoritma ini bergerak dengan mengunjungi seluruh child node dari kiri subtree. Apabila sudah habis, maka pencarian akan berlanjut ke child node dari kanan subtree. Outputnya berupa seluruh child di kiri -> root -> seluruh child di kanan

• Postorder Traversal

Algoritma ini bergerak dengan mengunjungi seluruh child node dari kiri subtree. Apabila sudah habis, maka pencarian akan berlanjut ke child node dari kanan subtree. Outputnya berupa seluruh child di kiri -> seluruh child di kanan -> root

Berikut adalah implementasi kode dalam bentuk C

#include <stdio.h>
#include <stdlib.h>

struct node {
   int data; 
	
   struct node *leftChild;
   struct node *rightChild;
};

struct node *root = NULL;

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;

      while(1) { 
         parent = current;
         
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }  //go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

struct node* search(int data) {
   struct node *current = root;
   printf("Visiting elements: ");

   while(current->data != data) {
      if(current != NULL)
         printf("%d ",current->data); 

      //go to left tree
      if(current->data > data) {
         current = current->leftChild;
      }
      //else go to right tree
      else {                
         current = current->rightChild;
      }

      //not found
      if(current == NULL) {
         return NULL;
      }
   }
   
   return current;
}

void pre_order_traversal(struct node* root) {
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}

void inorder_traversal(struct node* root) {
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);          
      inorder_traversal(root->rightChild);
   }
}

void post_order_traversal(struct node* root) {
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}

int main() {
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };

   for(i = 0; i < 7; i++)
      insert(array[i]);

   i = 31;
   struct node * temp = search(i);

   if(temp != NULL) {
      printf("[%d] Element found.", temp->data);
      printf("\n");
   }else {
      printf("[ x ] Element not found (%d).\n", i);
   }

   i = 15;
   temp = search(i);

   if(temp != NULL) {
      printf("[%d] Element found.", temp->data);
      printf("\n");
   }else {
      printf("[ x ] Element not found (%d).\n", i);
   }            

   printf("\nPreorder traversal: ");
   pre_order_traversal(root);

   printf("\nInorder traversal: ");
   inorder_traversal(root);

   printf("\nPost order traversal: ");
   post_order_traversal(root);       

   return 0;
}

Output yang dihasilkan adalah sebagai berikut

Visiting elements: 27 35 [31] Element found.
Visiting elements: 27 14 19 [ x ] Element not found (15).

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27