Stack adalah struktur data fundamental yang digunakan untuk menyimpan elemen secara linear (berurut). Stack mengikuti aturan LIFO (Last In, First Out) untuk melakukan operasinya. LIFO berarti elemen terakhir yang ditmabahkan ke dalam stack, akan menjadi elemen pertama yang akan dihapus. Cukup bayangkan saja tumpukan buku di atas meja. Buku yang terakhir ditumpuk (paling atas) akan menjadi buku pertama yang akan dikeluarkan dari tumpukan apabila ada operasi untuk menghapus elemen.

Berikut adalah ilustrasinya secara piktorial.

Seperti yang sudah diilustrasikan diatas, maka ketika kita ingin menambahkan item lain ke dalamnya, maka kita tambahkan item tersebut diatas tumpukan yang ada. Operasi ini dinamakan Push. Operasi push memiliki algoritma:

1. Memeriksa apakah Stack masih memiliki ruang.
2. Jika Stack sudah tidak memiliki ruang, hentikan operasi dan tampilkan pesan bahwa Stack sudah penuh.
3. Jika Stack masih memiliki ruang, tambahkan nilai pada atas tumpukan yang mengarahkan ke ruang kosong pada stack.
4. Menambahkan data pada ruang kosong yang ditunjuk.

Jika kita melakukan penghapusan item dari tumpukan, maka item yang akan dihapus adalah item yang paling atas. Operasi ini dinamakan Pop. Operasi ini memiliki algoritma operasi sebagai berikut:

1. Memeriksa apakah Stack memiliki isi
2. Apabila tidak berisi atau kosong, hentikan operasi dan tampilkan pesan bahwa Stack sudah kosong
3. Apabila Stack memiliki isi, maka akses data yang paling atas
4. Hapus atau kurangi nilai yang menunjuk ke data paling atas

Operasi lainnya yang ada pada Stack ini adalah sebagai berikut

1. peek --- untuk mengecek elemen paling atas pada stack, dan tidak melakukan modifikasi terhadapnya
2. isFull --- untuk melihat apakah Stack sudah penuh atau tidak memiliki ruang kosong
3. isEmpty --- untuk melihat apakah Stack sudah kosong atau tidak memiliki isi

Dalam hal inisialisasi kode untuk Stack pada C++, maka perlu diketahui beberapa bagian penting pada kode sebagai implementasi algoritma pada Stack.

1. Preprocessor dan Headerfile

#include <iostream>
#define MAX 10
using namespace std;

Stack memiliki Standard Library (STL) khusus pada C++, yaitu <stack>, namun kita juga bisa menggunakan header iostream untuk melakukan algoritma Stack, dan MAX sebagai nilai maksimum array pada stack

2. Struct

struct Stack {
	int top, data[MAX];
}Tumpukan

Deklarasi struct berisi top yang akan menjadi nilai data yang ada di paling atas tumpukan, dan array bernama data[] untuk inisialisasi array sebagai Stack dengan besaran MAX

3. Insialisasi nilai top

void init(){
	Tumpukan.top = -1;
}

Nilai top sendiri diinisialisasi sebagai -1, karena data pertama yang ada pada stack, akan ber-indeks 0. Nilai -1 juga akan menjadi nilai kondisi Stack yang kosong

4. Pengecekan stack

Fungsi-fungsi berikut berfungsi untuk mengecek keadaan stack, apakah Stack dalam keadaan kosong atau penuh.

bool isEmpty() {
  return Tumpukan.top == -1;
}

bool isFull() {
	return Tumpukan.top == MAX-1;
}

Fungsi isEmpty() sendiri akan mengembalikan nilai true (karena tipe data yang digunakan adalah boolean) jika nilai nya -1, dan false apabila tidak sama dengan 1. Fungsi isFull() akan mengembalikan nilai true jika nilai top adalah MAX(ukuran maksimal arrray) dikurangi 1 (karena indeks array dimulai dari 0), dan false apabila tidak sama.

5. Menambahkan data ke stack

void push() {
   if (isFull()) {
		cout << "\nTumpukan penuh"<<endl;
	}
	else {
    Tumpukan.top++;
    cout << "\nMasukkan data = "; cin >> Tumpukan.data[Tumpukan.top];
    cout << "Data " << Tumpukan.data[Tumpukan.top] << " masuk ke stack"<<endl;
	}
}

Dalam hal menambahkan data ke stack, maka algoritma yang perlu diperhatikan adalah

• Cek terlebih dahulu apakah Stack sudah penuh, jika penuh, maka hentikan.
• Jika tidak penuh, maka lakukan increment nilai top
• Masukkan data ke dalam tempat yang diarahlan oleh top

6. Menghapus data dari stack

void pop() {
	if (isEmpty()) {
		cout << "\nData kosong\n"<<endl;
	}
	else {
    cout << "\nData "<<Tumpukan.data[Tumpukan.top]<<" sudah terambil"<<endl;
    Tumpukan.top--;
	}
}

Mirip dengan menambahkan data, ada algoritma yang perlu diperhatikan ketika ingin menghilangkan data dari stack, yaitu:

• Periksa apakah Stack kosong, jika kosong, maka hentikan.
• Jika tidak kosong, maka lakukan decrement pada nilai top untuk menghapus data

7. Menampilkan data pada tumpukan

void printStack() {
	if (isEmpty()) {
		cout << "Tumpukan kosong";
	}
	else {
    cout << "\nTumpukan : ";
		for (int i = Tumpukan.top; i >= 0; i--)
			cout << Tumpukan.data[i] << ((i == 0) ? "" : ",");
	}
}

Dalam menampilkan data, algoritmanya adalah sebagai berikut:

• Periksa apakah Stack kosong, jika kosong, maka hentikan.
• Jika tidak kosong, maka lakukan penampilan data satu-persatu menggunakan perulangan atau looping

Berikut adalah contoh kodingan Stack menggunakan C++

#include <iostream>
using namespace std;
#define MAX 100

class Stack
{
    int top;

public:
    int myStack[MAX];

    Stack() { top = -1; }
    bool push(int x);
    int pop();
    bool isEmpty();
};

bool Stack::push(int item)
{
    if (top >= (MAX - 1))
    {
        cout << "Stack Penuh";
        return false;
    }
    else
    {
        myStack[++top] = item;
        cout << item << endl;
        return true;
    }
}

int Stack::pop()
{
    if (top < 0)
    {
        cout << "Stack Underflow";
        return 0;
    }
    else
    {
        int item = myStack[top--];
        return item;
    }
}

bool Stack::isEmpty()
{
    return (top < 0);
}

int main()
{
    class Stack stack;
    cout << "Add Stack" << endl;
    stack.push(2);
    stack.push(4);
    stack.push(6);
    cout << "Remove Item From Stack : " << endl;
    while (!stack.isEmpty())
    {
        cout << stack.pop() << endl;
    }
    return 0;
}

Dikarenakan Stack memiliki header sendiri, maka kita bisa menggunakan fungsi-fungsi yang ada di headernya secara langsung dan tidak perlu dibuatkan fungsi tersendiri. Lengkapnya bisa dicek di GeeksForGeeks yang membahasnya dengan cukup baik.

Pada dasarnya, fungsi yang ada pada header <stack> tidak berbeda jauh baik dari algoritma, fungsi, hingga penamaan dengan fungsi yang dibuat manual seperti contoh kode diatas. Implementasi Stack menggunakan bantuan header <stack> adalah sebagai berikut.

#include <iostream>
#include <stack>
using namespace std;
int main() {
    stack<int> stack;
    stack.push(21);
    stack.push(22);
    stack.push(24);
    stack.push(25);
    int num=0;
    stack.push(num);
    stack.pop();
    stack.pop();
    stack.pop();
   
    while (!stack.empty()) {
        cout << stack.top() <<" ";
        stack.pop();
    }
}

Materi ini diberikan pada pertemuan pertama struktur data, dimana postfix dan infix sendiri merupakan sebuah ekspresi pada operator, dimana infix merupakan ekspresi dimana bentuk operand-operator-operand, atau operator yang berada di antara operand (a+b), dan postfix merupakan ekspresi dimana bentuk operator-operator-operand dimana operator dituliskan setelah operand selesai dituliskan.

Input: A + B * C + D
Output: ABC*+D+

Input: ((A + B) – C * (D / E)) + F
Output: AB+CDE/*-F+  

Algoritma yang dapat dilakukan untuk mengubah ekspresi infix menjadi expresi postfix adalah sebagai berikut

Anggap, X adalah sebuah ekspresi aritmatika yang ditulis dalam notasi infix, dan algoritma mencari ekspresi matematika yang ekuivalen dengan notasi postfix, yang dilambangkan sebagai Y

1. Masukkan "(" pada stack, dan tambahkan ")" di akhir stack
2. Lakukan pengecekan pada X dari kiri ke kanan, dan ulangi langkah 3 sampai 6 sampai stack kosong
3. Apabila operand ditemukan, maka tambahkan ke Y
4. Apabila kurung buka ditemukan, maka tambahkan ke stack
5. Apabila operator ditemukan, maka

• Lakukan perulangan pada proses pop dari stack dan tambahkan setiap operator ke Y (diatas stack) yang memiliki kedudukan yang sama, atau lebih tinggi
• Tambahkan operator ke stack

6. Apabila kurung tutup ditemukan, maka

• Lakukan perulangan pada proses pop dari stack dan tambahkan setiap operator ke Y (diatas stack) sampai kurung buka ditemukan
• Hilangkan kurung buka

7. END

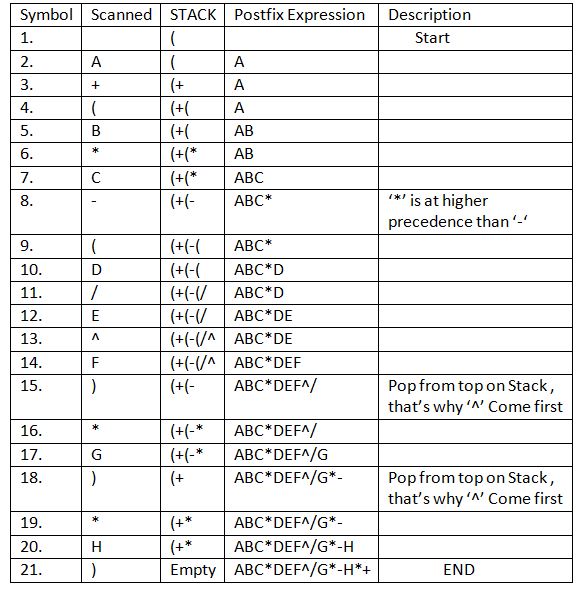
Berikut adalah contoh ekspresi infix A+ (B*C-(D/E^F)*G)*H yang diubah ke postfix, dimana ^ merupakan operator eksponensial

#include<stdio.h>
#include<ctype.h>

char stack[100];
int top = -1;

void push(char x)
{
    stack[++top] = x;
}

char pop()
{
    if(top == -1)
        return -1;
    else
        return stack[top--];
}

int priority(char x)
{
    if(x == '(')
        return 0;
    if(x == '+' || x == '-')
        return 1;
    if(x == '*' || x == '/')
        return 2;
    return 0;
}

int main()
{
    char exp[100];
    char *e, x;
    printf("Enter the expression : ");
    scanf("%s",exp);
    printf("\n");
    e = exp;
    
    while(*e != '\0')
    {
        if(isalnum(*e))
            printf("%c ",*e);
        else if(*e == '(')
            push(*e);
        else if(*e == ')')
        {
            while((x = pop()) != '(')
                printf("%c ", x);
        }
        else
        {
            while(priority(stack[top]) >= priority(*e))
                printf("%c ",pop());
            push(*e);
        }
        e++;
    }
    
    while(top != -1)
    {
        printf("%c ",pop());
    }return 0;
}

Output:

Enter the expression : a*b(c-d)
a b c d - * 

Enter the expression : 5/3(7+(8*4)-2)
5 3 7 8 4 * + 2 - /