1 4 透過數位邏輯電路學習 Bitwise 操作 - ianchen0119/AwesomeCS GitHub Wiki

關於 CPU 的設計要點，我們可以透過維基百科略知一二:

處理器設計關注：

• 數據路徑 (如ALU 和 計算管道)
• 控制單元：邏輯控制的數據路徑
• 記憶體元件，如暫存器文件緩存
• 時脈電路，如時脈驅動器，PLL，時鐘分配網絡
• 墊收發器電路
• 邏輯閘電路的實現 -- wikipedia

本篇文章要從邏輯閘做為起點，一路探討到 C 語言上的 Bitwise 操作。

邏輯閘

NOT

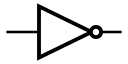
• 功能

NOT gate 可以做到反相的用途，也就是把 1 變成 0 、 0 變成 1。

• CMOS 電路

CMOS 已經被廣泛應用在積體電路上，下圖是使用 PMOS + NMOS 組合而成的 NOT gate 電路。

關於積體電路，可以在這邊參考更多。

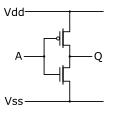
if A = Vdd :
    PMOS = cutoff;
    NMOS = on;
    Q = 0v;
if A = 0v :
    PMOS = on;
    NMOS = cutoff;
    Q = Vdd;

說來慚愧，前陣子去面試交大資工實務組時，性向測驗有考到什麼是 CMOS，我竟然連這麼簡單的問題都答不清楚，有愧於我是電子工程系出來的學生阿 : )

• 真值表

Input	Output
0	1
1	0

OR

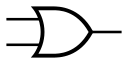
• 功能

簡單來說，OR gate 的功能就是檢查輸入是否有 1 ;如果有，就輸出 1，否則為 0。

• 真值表

Input 1	Input 2	Output
0	0	0
0	1	1
1	0	1
1	1	1

AND

• 功能

AND Gate 就是邏輯上的兩者相乘，輸入都是 1 時，輸出才是 1。

• 真值表

Input 1	Input 2	Output
0	0	0
0	1	0
1	0	0
1	1	1

XOR

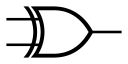
• 功能

XOR Gate 中文為互斥或閘，筆者自己的理解是: 檢查輸入是否相異，如果相異，輸出為 1，否則為 0。

• 真值表

Input 1	Input 2	Output
0	0	0
0	1	1
1	0	1
1	1	0

本篇接續上一篇繼續介紹 Bitwise 、移位以及布林函數。

Bitwise 基本操作

前一篇文章我們已經介紹了基本的邏輯閘，本篇要介紹的是 Bitwise 操作。 至於為什麼要將數位邏輯電路以及 Bitwise 一併介紹則是因為 Bitwise 操作與常用邏輯閘所做到的功能是一樣的。

NOT

在 C 語言中(或是其他語言)以 ~ 表示反向。

int x = 1;
int y = ~x;// 0

AND

在 C 語言中(或是其他語言)以 & 表示及運算。

int x = 1;
int y = ~x;// 0
int z = x & y;// 0

OR

在 C 語言中(或是其他語言)以 | 表示或運算。

int x = 1;
int y = ~x;// 0
int z = x | y;// 1

XOR

在 C 語言中(或是其他語言)以 ^ 表示互斥或運算。

int x = 1;
int y = ~x;// 0
int z = x ^ y;// 1

小試身手

介紹完 bitwise 後，我們可以利用刷題檢驗學習成效。

題目: power-of-two。

解答

1. 一行版本:

return n > 0 && (n & (n - 1)) == 0;

• 解題思維:
  • 2 的 n 次方無法表示出負數，所以輸入值需要大於 0。
  • 參考。

2. 優化版本

bool isPowerOfTwo(int n){
    if(n == 1) return true;
    if(n & 1) return false;
    return n > 0 && (n & (n - 1)) == 0;
}

• 解題思維:
  • 除了 1 以外，奇數不可能為 2 的 n 次方。 因此，我們利用 AND 運算判斷輸入值是否為奇數:

  if(n == 1) return true;
  if(n & 1) return false;
  

經過優化後，在 leetcode 上面的執行時間從 4ms 下降至 0ms，順利達到速度最佳化的目標。

移位

移位是一個二元運算子，能夠將一個二進位數中的每一位全部都向一個方向移動指定位(溢位的部分會被捨棄)，而空缺的部分補 0。 在 C 語言中，左移使用 << 表示，右移則使用 >> 表示。

邏輯左移

捨棄高位，低位補 0。

   0001（十進制 1 ）
<<     （左移 1 位）
 = 0010（十進制 2 ）

  0001（十進制 1 ）
<<4    （左移 4 位）
= 0000（十進制 0 ） -> overflow

邏輯右移

捨棄低位，高位補 0。

  0100（十進制 4 ）
>>    （右移 1 位）
= 0010（十進制 2 ）

算術右移

除了邏輯位移 (Logical shift) 外，還有算術位移 (Arithmetic shift) 它與邏輯位移的差異就是會在最左側補上號數 (sign bit) 的值。

如果讀者看過先前介紹的數值系統，就會知道若今天我們所存放的變數是含正負號的整數，它會在 MSB (高位) 占用一個 bit 去辨別正負號 (0 為正，1 為負)。

  11110（十進制 -14 ）
>>    （右移 1 位）
= 11111（十進制 -15 ）

在 C 語言中，對於有號數的操作都是以邏輯左移 + 算術右移為主。

實際上還是需要參考你所使用的編譯器是如何實作。

若我們想要在 C 語言實現邏輯右移，可以將變數轉為無號數再做操作:

int mian()
{
    int n = 0xfffffffe;
    int m = (unsigned int)n >> 1;
    printf("0x%x\n", m);
}

那個...算術左移呢?

為什麼剛剛都沒有提到算術左移呢? 筆者舉兩個例子方便解說:

• 對正數來說 (signed-bit = 0) 向左移也還是正數，若變成負數則代表該數值已經 overflow 了。
• 對負數來說 (signed-bit = 1) 由於負數會用 2 的補數表示，所以前面都是 1。 若 offset 超過了代表該數值也是有問題的。

邏輯左移和算術左移並沒有任何差異，不像是右移時需要考慮 signed-bit 的問題。就本質上來說，兩者所做的事情根本一模一樣。因此，剛剛才沒有介紹算術左移 XD

小總結

移位的效果幾乎等效於乘法/除法。對電腦硬體來說，乘除法屬於複雜運算，需要使用多條指令才能做到。若我們熟悉位移操作，便能將原先要多條指令才能做到的事情簡化成用一條指令達成，有助於撰寫出更高效的程式碼。

特殊情況可以參考這裡。

此外，若讀者想測驗一下自己對 Bitwise 的操作是否熟練，可以在該網站小試身手。

如果覺得這些都太簡單，可以參考 Jserv 的 Bitwise 教學。

布林函數

圖片取自 wikipedia。

上圖是一個二選一的數據多工器，他的布林函數如下:

我們可以利用剛剛所學的 Bitwise 操作，在 C 語言寫出與上面布林函式等效的表達式:

bool z = (A & ~S) | (B & S);

• 真值表

S	A	B	Z
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

這個真值表表示:

• 當 S = 0 時，Z = A。
• 當 S = 1 時，Z = B。

當然，我們也可以透過 C 語言表達式和布林函數推敲出這個結果。

此外，我們回到剛剛寫下的 C 語言表達式:

bool z = (A & ~S) | (B & S);

一共用了 4 個運算符號，從左至右分別是 & 、 ~ 、 | 、 &。 我們可以把一個運算符號當成一個邏輯閘，這也代表我們可以用兩個 AND gate 、一個 NOT gate 以及一個 OR gate 兜出一個二擇一多工器唷!

參考邏輯閘電路。

總結

讀完本篇章，讀者可以迅速掌握基礎邏輯閘的功能並且學會 Bitwise 操作，有利於我們撰寫出更高效的 C 語言程式。

本篇中的邏輯閘圖片都是取自維基百科。

延伸閱讀

1. 如果對於 CMOS 數位邏輯有興趣，可以看看中興物理的應用電子學講義。
2. 更多 Bitwise 的應用