O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!)

#include <cstdio>
using namespace std;
 
int main(){
    int N, sum = 0;
    scanf("%d", &N);
    for(int i=1; i<=N; i++)
        sum += i;
    printf("%d\n", sum);
}


#include <cstdio>
using namespace std;
 
int main(){
    int N, M;
    scanf("%d %d", &N, &M);
    for(int i=0; i<N; i++)
        for(int j=0; j<M; j++)
            printf("%d %d\n", i, j);
}


#include <cstdio>
using namespace std;
 
int main(){
    int N;
    scanf("%d", &N);
    for(int i=0; i<N; i++)
        for(int j=0; j<N; j++)
            printf("%d %d\n", i, j);
}

입력의 크기를 시간 복잡도에 대입해서 얻은 반복문 수행 횟수에 대해, 1초 당 반복문 수행 횟수가 1억(108)을 넘어가면 시간 제한을 초과할 가능성이 있다.

1<N<100,000,000

1초는 대략 1억번

천만 ⇒ 1초의 제한시간에 넉넉

10억번 무리!

int ⇒ 4byte -(2^31) ~ ( 2^31 - 1 )

char ⇒ 1byte

long long ⇒ 8byte ( 2^63 ) ~ ( 2^63 - 1 )

double ⇒ 8byte ( 1.7E-308 ~ 1.7E+308 )

bool ⇒ 1byte

1KB = 2^10 byte ~ 대략 int 2^6개 ⇒ 64개

1MB = 2^10KB ~ 대략 int 1024*(2^6) 개 ⇒ 대략 int 60000개

1GB = 2^10MG ~ 대략 int 1024*(2^16)개 ⇒ 대략 int 60000000 개

용량 50000 * 50000 character char배열이있다.

25*10^8 Byte

⇒ 2.5 GB

2^10 = 1024 =>1000

256MB 메모리 제한이 있어요~~ int를 !대략! 몇개까지 만들어도 될까?

2^8* 1000 * 1000 byte / 4 byte = 2^6 * 1000 * 1000

2^10 kbytes => 1000

2^10 bytes => 1000

(2^8*1000,000)byte / 4 byte = 2^6 * 1000,000 개 만들어도 된다!

각각의 무게를 가진 9개의 금이 있다.

1kg, 2kg, 3kg, 12kg, 15kg, 9g, 7kg, 8kg, 6kg

이중에 3개를 골라서 가장 무거운 금의 합을 만들라

=> 해결법은?

회의실 배정

1. 회의가 짧은 순서
2. 일찍 시작하는 순서
3. 일찍 끝나는 순서

       -----
  -------  --------


    -------  ----- 
  --------------------------



  -----     ----
     -------   --------
---------------   -------
     -------------            ------
         ------------
              -------------
                     ---------
  -------------------------------



[출처] https://kim6394.tistory.com/67

주어진 문제를 여러개의 부분문제로 나누어 푼다음, 주어진 문제를 푼다.

O(n)

https://www.acmicpc.net/problem/9465

점화식

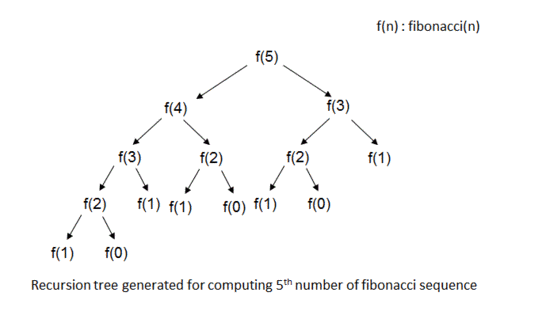
피보나치!

f(0) = 0

f(1) = 1

f(n) = f(n-1)+f(n-2)

$$Fib(n) = { ({1+\sqrt{5}\over2})^2 - ({1-\sqrt{5}\over2})^2 \over\sqrt5}$$

int fibo(int n){
	if (n==0)      return 0;
	else if (n==1)     return 1;
	else return fibo(n-1)+fibo(n-2);
}

[출처] 동적 계획법(Dynamic Programming) (수정: 2019-02-07)|작성자 라이

int fibo(int n){
	if (n==0)      return 0;
	else if (n==1)     return 1;
	else
		if(cache[n]==-1)
		cache[n]=fibo(n-1)+fibo(n-2);
		
		return cache[n];
}

    for(int i=0; i<=N; i++){
        dp[i+2] += dp[i];
        dp[i+1] += dp[i];
    }
    
[출처] 동적 계획법(Dynamic Programming) (수정: 2019-02-07)|작성자 라이

그래서 DP란? 주어진 문제를 여러개의 부분문제를 나누어 푼다음 그결과로 다음것을 푸는것

3
0 : 26 40 83
1 : 49 60 57
2 : 13 89 99

0:r 1:g 2:b
#include <algorithm>

0 1 2

** in[house][color]
in[0][0] = 26
in[0][1] = 40
in[0][2] = 83
in[1][0] = 49


/  \  /  \   /  \
| 0|  |1 |  |2 |
** house[house index][color]

house[0][0] = in[0][0] //26
house[0][1] = in[0][1] //40
house[0][2] = in[0][2] //83

for(int i=1 ; i<n ; i++)
{
	house[i][0] = in[i][0] + min(house[i-1][1], house[i-1][2]);
  house[i][1] = in[i][1] + min(house[i-1][0], house[i-1][2]);
  house[i][2] = in[i][2] + min(house[i-1][0], house[i-1][1]);
}

min(<int>,<int>);

printf("%d", min(house[n-1][0], min(house[n-1][1], house[n-1][2] ));