1. Definisi Operasi Matriks

Operasi pada matriks adalah sekumpulan operasi matematika yang yang diterapkan kepada susunan nilai yang disusun dalam bentuk tabel 2 dimensi yang terdiri dari baris dan kolom. Adapun operasi matriks ini sendiri digunakan untuk menyelesaikan banyak permasalahan seperti sistem persamaan linear dan menghitung statistik.

Contoh dari Matriks adalah sebagai berikut:

Eh salah😅

Dapat kita lihat pada contoh di atas, matriks adalah sekumpulan nilai dalam bentuk 2 dimensi yang disusun dalam baris dan kolom. Dalam implementasinya di python, kita akan menggunakan array multimensional pada numpy yang telah dipelajari pada pertemuan sebelumnya. Adapun yang akan kita pelajari hari ini terdiri dari:

1. Membuat matriks
2. Operasi matriks dengan bilangan skalar
3. Penjumlahan dan Pengurangan Matriks
4. Perkalian matriks
5. Transpose matriks
6. Invers matriks
7. Determinan matriks
8. Penyelesaian persamaan linear menggunakan matriks

2. Operasi Matriks

2.1 Membuat Matriks

Untuk membuat matriks dapat kita lakukan dengan membuat array 2 dimensi menggunakan library numpy. Mungkin sudah diketahui bahwa untuk membuat multidemensional array dapat dilakukan dengan:

a = np.array([baris 1],[baris 2](/fzl-22/modul-alstrukdat-sainsdata/wiki/baris-1],[baris-2))

Namun agar pendefinisiannya lebih ke matriks matriks an kita dapat mendefinisikan/membuat matrik dengan sebagai berikut:

a = np.matrix([baris 1],[baris 2](/fzl-22/modul-alstrukdat-sainsdata/wiki/baris-1],[baris-2))
a = np.matrix([9,10],[11,12](/fzl-22/modul-alstrukdat-sainsdata/wiki/9,10],[11,12))

# Atau

a = np.matrix('baris 1;baris 2;baris 3')
b = np.matrix('1,2;3,4;5,6')

Output:

[[ 9 10]
 [11 12]]

[[1 2]
 [3 4]
 [5 6]]

2.2 Operasi Matriks dengan Bilangan Skalar

Operasi matriks dengan bilangan skalar adalah operasi matematika yang melibatkan matriks dengan bilangan skalar atau bilangan yang hanya memiliki nilai tunggal tanpa arah atau bukan vektor. Operasi matriks dengan bilangan skalar dilakukan dengan menerapkan operasi matematika pada setiap element matriks dengan bilangan skalar. Untuk melakukannya pada python dapat dilakukan langsung sebagai berikut:

print(f"perkalian   = \n{5 * np.array([1,2,3],[4,5,6](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,2,3],[4,5,6))}\n")
print(f"penjumlahan = \n{5 + np.array([1,2,3],[4,5,6](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,2,3],[4,5,6))}\n")
print(f"pengurangan = \n{5 - np.array([1,2,3],[4,5,6](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,2,3],[4,5,6))}\n")
print(f"pembagian   = \n{5 / np.array([1,2,3],[4,5,6](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,2,3],[4,5,6))}\n")

Output:

perkalian   = 
[[ 5 10 15]
 [20 25 30]]

penjumlahan = 
[[ 6  7  8]
 [ 9 10 11]]

pengurangan = 
[[ 4  3  2]
 [ 1  0 -1]]

pembagian   = 
[[5.         2.5        1.66666667]
 [1.25       1.         0.83333333]]

Dapat dilihat dari output di atas hasil dari operasi skalar adalah sebuah matriks dengan jumlah anggota yang sama dengan nilai tiap - tiap anggotanya telah dikenai operasi matematika dengan nilai skalar yang pada kasus di atas adalah 5.

2.3 Penjumlahan dan Pengurangan Matriks

Penjumlahan pada matriks memiliki aturan yaitu matriks yang dijumlahkan haruslah memiliki bentuk yang sama atau memiliki jumlah baris dan kolom yang sama. Hal tersebut dikarenakan operasi penjumlahan dan pengurangan antar matriks dilakukan dengan menjumlahkan penjumlahan atau pengurangan antar elemen yang memiliki posisi yang sama. Agar lebih jelas perhatikan ilustrasi berikut:

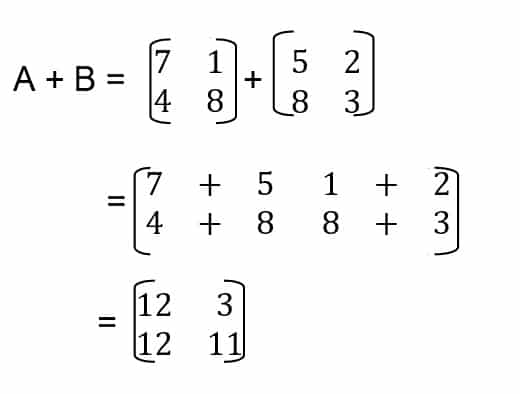
Dapat dilihat pada ilustrasi di atas bahwa penjumlahan dilakukan antar element yang memiliki anggota yang sama. Untuk mengimplementasikan hal tersebut di dalam pemrograman kita bisa melakukannya dengan a + b saja atau menjumlahkan matriks pada python dapat menggunakan method add pada numpy:

np.add(matriks1,matriks2)

# Contoh:
np.add(np.matrix([1,2,3],[4,5,6](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,2,3],[4,5,6)),np.matrix([7,8,9],[10,11,12](/fzl-22/modul-alstrukdat-sainsdata/wiki/7,8,9],[10,11,12)))
np.add(np.add(np.array([1,2,3],[4,5,6](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,2,3],[4,5,6)), np.matrix([7,8,9],[10,11,12](/fzl-22/modul-alstrukdat-sainsdata/wiki/7,8,9],[10,11,12))),np.matrix([1,1,1],[1,1,1](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,1,1],[1,1,1)))

Contoh:

matrix([[ 8, 10, 12],
        [14, 16, 18]])

matrix([[ 9, 11, 13],
        [15, 17, 19]])

Untuk mengurangi antar matriks maka dapat dilakukan dengan method subtract.

np.subtract(matriks1,matriks2)

# Contoh:
np.subtract(np.matrix([1,2,3],[4,5,6](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,2,3],[4,5,6)),np.matrix([7,8,9],[10,11,12](/fzl-22/modul-alstrukdat-sainsdata/wiki/7,8,9],[10,11,12)))
np.subtract(np.subtract(np.array([1,2,3],[4,5,6](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,2,3],[4,5,6)), np.matrix([7,8,9],[10,11,12](/fzl-22/modul-alstrukdat-sainsdata/wiki/7,8,9],[10,11,12))),np.matrix([1,1,1],[1,1,1](/fzl-22/modul-alstrukdat-sainsdata/wiki/1,1,1],[1,1,1)))

Output:

matrix([[-6, -6, -6],
        [-6, -6, -6]])

matrix([[-7, -7, -7],
        [-7, -7, -7]])

Sebenarnya kita dapat melakukan penjumlahan terhadap matriks yang memiliki dimensi yang berbeda pada numpy, namun hal tersebut menyalahi aturan dari operasi matriks yang sebenarnya.

2.3 Perkalian Matriks

Perkalian pada matriks adalah sesuatu yang berbeda dengan penjumlahan/pengurangan. Hal tersebut karena aturan dari perkalian matriks pertama adalah jumlah baris dari matriks pengali haruslah sama dengan jumlah kolom matriks yang akan dikalikan. Agar lebih jelas maka perhatikan ilustrasi berikut:

Dapat dilihat pada gambar di atas, matriks hasil pada posisi [0,0] berasal dari penjumlahan pengalian antar element yang kemudian dijumlahkan sehingga matriks hasil dari perkalian akan memiliki jumlah baris yang sama dengan matriks a dan jumlah kolom yang sama dengan matriks b. Contoh jika matriks a berukuran 2x3 dan b berukuran 3x4 maka akan mengasilkan matriks baru dengan ukuran 2x4

Pada gambar di atas dijelaskan bahwa perkalian pada matriks tidak dilakukan dengan mengalikan antar element yang memiliki indeks yang sama sehingga hasil yang akan didapatkan dengan hanya melakukan a * b adalah hasil yang bernilai salah karena a * b akan mengalikan antar element matriks saja. Namun untuk mengalikan matriks dapat menggunakan method numpy yaitu dot atau dengan simbol @. Hal tersebut dapat dibuktikan sebagai berikut:

A = np.array([  [1, 2], 
                [4, 5]]) #matriks 2x2

B = np.array([  [7, 8], 
                [11, 12]]) #matriks 2x2

C = np.dot(A, B)  # menggunakan fungsi np.dot()
D = A @ B         # menggunakan operator "@"

print(C,end='\n\n')
print(D,end='\n\n')
print(A * B)

Output:

[[29 32]
 [83 92]]

[[29 32]
 [83 92]]

[[ 7 16]
 [44 60]]

Dapat dilihat bahwa hasil dari output dot dan @ berbeda dengan menggunakan * saja. Untuk itulah kita harus menggunakan dot atau @ ketika ingin mengalikan matriks.

2.4 Tranpose Matriks

Tranpose matriks adalah bentuk manipulasi matriks dengan merubah baris menjadi kolom dan sebaliknya. Contoh:

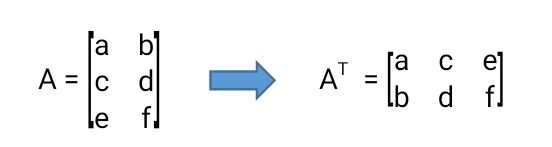
Untuk melakukannya pada numpy maka cukup mudah, hanya gunakan method tranpose atau T. Contoh:

B = np.array([  [7, 8, 9, 10], 
                [11, 12, 13, 14], 
                [15, 16, 17, 18]])

print(B,end="\n\n")

print(B.transpose(),end="\n\n")

print(B.T,end="\n\n")

Output:

[[ 7  8  9 10]
 [11 12 13 14]
 [15 16 17 18]]

[[ 7 11 15]
 [ 8 12 16]
 [ 9 13 17]
 [10 14 18]]

[[ 7 11 15]
 [ 8 12 16]
 [ 9 13 17]
 [10 14 18]]

2.5 Invers Matriks

Matriks invers secara sederhana dapat disebut dengan matriks kebalikan. Namun, untuk mencari invers matriks tidak sesederhana membalikkan posisi dari element matriks seperti transpose. Matriks invers sendiri dapat diketahui dengan jika matriks dikalikan dengan inversnya maka akan menghasilkan matriks identitas. Lantas apa itu matriks identitas? sederhannya maatriks identitas adalah matriks yang diagonalnya memiliki nilai 1 dan sisanya bernilai 0.

Untuk mencari invers dari matriks melalui jalur pemrograman maka dapat dilakukan dengan menggunakan method np.linalg.inv. Namun perlu diketahui, matriks yang dapat diinvers hanya matriks persegi atau jumlah baris sama dengan jumlah kolomnya dan determinannya tidak 0. Contoh:

B = np.array([  [1, 2, 3], 
                [11,1, 5], 
                [23, 4, 21]])

C = np.linalg.inv(B)

identity = np.dot(B,C)

print("B :\n",B)
print("\nB_INVERS :\n",C)
print("\nB * B_INVERS :\n",identity)

Output:

B :
 [[ 1  2  3]
 [11  1  5]
 [23  4 21]]

B_INVERS :
 [[-0.00595238  0.17857143 -0.04166667]
 [ 0.69047619  0.28571429 -0.16666667]
 [-0.125      -0.25        0.125     ]]

B * B_INVERS :
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

2.6 Determinan Matriks

Determinan matriks merupakan sebuah bilangan yang dapat dihasilkan oleh matriks persegi. Nilai determinan ini dapat digunakan untuk menentukkan apakah sebuah matriks persegi memiliki invers atau tidak yaitu jika determinan matriks persegi = 0 maka dapat dipastikan bahwa matriks tersebut tidak memiliki invers meskipun matriksnya berbentuk persegi.

Untuk mencari nilai determinan matriks pada python dapat dilakukan dengan np.linalg.det(matriks):

# Definisikan matriks
A = np.array([3, 4], [5, 6](/fzl-22/modul-alstrukdat-sainsdata/wiki/3,-4],-[5,-6))

# Hitung determinan matriks
det_A = np.linalg.det(A)

# Tampilkan hasil
print("Matriks A:\n", A)
print("Determinan A: ", det_A)

Output:

Matriks A:
 [[3 4]
  [5 6]]
Determinan A:  -2.0000000000000018

2.7 Penyelesaian Permasalahan Persamaan Linear dengan Matriks

Matriks dapat menyelesaikan permasalahan persamaan linear yaitu pencarian solusi dengan mencari nilai dari variabel yang menyusun sebuah persamaan. Contoh persamaan linear adlaah sebagai berikut:

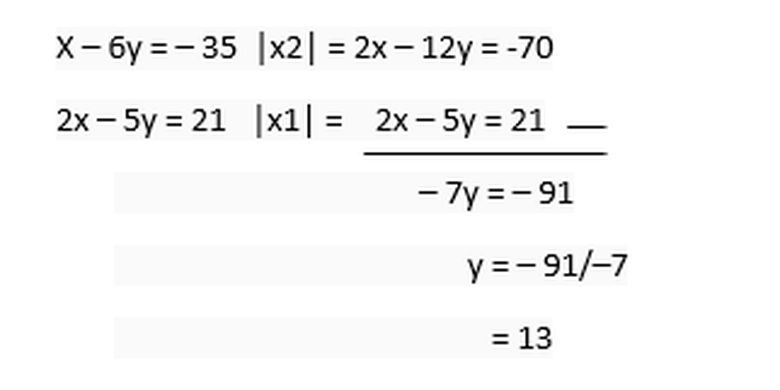
Dengan menggunakan numpy maka permasalahan tersebut sangat mudah untuk diselesaikan, yaitu dengan method np.linalg.solve. Untuk menggunakannya maka perhatikan contoh berikut:

# Misalkan kita memiliki persamaan:
# 3x + 2y - z = 1
# x - y + 2z = -2
# 2x + y + 3z = 3

# Matriks koefisien
A = np.array([2, -2, -2], [1, -6, -3], [3, 2, 1](/fzl-22/modul-alstrukdat-sainsdata/wiki/2,--2,--2],-[1,--6,--3],-[3,-2,-1)) # bagian yang mengandung variabel

# Vektor hasil
B = np.array([9, -28, 16]) # hasil persamaan

# Menyelesaikan sistem persamaan linear
X = np.linalg.solve(A, B)

# Menampilkan solusi
print("Solusi:")
print("x =", X[0])
print("y =", X[1])
print("z =", X[2])

Output:

Solusi:
x = 2.0
y = 12.5
z = -15.0