Algoritma sorting merupakan sebuah metode untuk mengatur susunan dari objek-objek (bisa berupa angka, karakter, hingga string) dalam susunan yang terurut. Susunan yang dimaksud dapat terurut secara ascending (dari urutan terbesar ke terkecil) atau descending (dari urutan terbesar ke terkecil).

Contoh,

myList = [10, 7, 9, 1, -2, 6, 0] # data tidak terurut

Menjadi:

myList = [-2, 0, 1, 6, 7, 9, 10] # ascending
myList = [10, 9, 7, 6, 1, 0, -2] # descending

Dalam bahasa Python, mengurutkan suatu list dapat dengan mudah dilakukan dengan memanggil method .sort() yang sudah disediakan secara built-in, seperti kode program di bawah ini:

myList.sort() # ascending
myList.sort(reverse=True) # descending

Tetapi, perlu digarisbawahi bahwa pada modul ini kita tidak belajar untuk memanggil fungsi/method. Melainkan kita akan belajar membuat fungsi sendiri untuk melakukan pengurutan menggunakan beberapa algoritma berikut:

1. Bubble Sort
2. Insertion Sort
3. Quick Sort
4. Merge Sort

1. Algoritma Bubble Sort

Algoritma bubble sort merupakan algoritma sorting yang idenya paling sederhana, tetapi tidak efisien. Algoritma ini bekerja dengan cara menukar elemen-elemen bersebelahan yang tak terurut secara berulang-ulang. Visualisasi dari algoritma ini dapat dilihat di di sini. Perhatikan bahwa algoritma ini bekerja seperti gelembung, dalam hal algoritma ini membawa elemen terbesar satu-persatu ke ujung array. Secara lebih detail, langkah-langkahnya aja seperti berikut:

1. Lakukan perulangan pada setiap elemen pada array A
2. Pada setiap iterasi, lacak pertukaran elemen dengan mendefinisikan variabel swapped bernilai False
3. Kemudian, lakukan perulangan dari indeks j=0 hingga index (len(A) - i - 1) , karena indeks paling belakang akan menjadi tempat untuk nilai terbesar.
4. Pada setiap iterasi perulangan pada poin 3, bandingkan nilai A[j] dan A[j + 1] . Apabila A[j] lebih besar, tukar nilai kedua elemen tersebut.
5. Setelah pertukaran, berikan tanda bahwa sudah terjadi pertukaran dengan mengganti nilai variabel swapped menjadi True.
6. Jika tidak ada swapping sama sekali setelah perulangan pada poin 3 (artinya variabel swapped tetap bernilai False), maka hentikan looping pada poin 1 karena setiap elemen sudah jelas terurut.

Berikut adalah ilustrasi langkah-langkah algoritma bubble sort:

Berikut adalah implementasinya dalam Python:

def bubbleSort(A):
	for i in range(len(A)):
		swapped = False
		for j in range(0, len(A) - i - 1):
			if A[j] > A[j + 1]: # coba ganti tandanya menjadi <, apa yang terjadi?
				A[j], A[j + 1] = A[j + 1], A[j]
				swapped = True
		if not swapped:
			break

A = [9, -3, 5, 2, 6, 8, -6, 1, 3]
bubbleSort(A)
print(A)

Algoritma ini dikatakan tidak efisien karena pada kasus terbaik dan kasus rata-rata, algoritma ini membutuhkan sebanyak $O(N^2)$ langkah komputasional untuk array sepanjang $N$ element. Artinya, katakanlah kita memiliki sebuah array tak terurut sepanjang 100 elemen, maka algoritma ini membutuhkan kira-kira sebanyak $100^2=10000$ langkah komputasi.

Pada kasus terbaik (yaitu array sudah terurut), algoritma ini memerlukan sebanyak $O(N)$ langkah komputasional (walaupun efisien, tapi seberapa mungkin kita mendapatkan elemen yang sudah terurut untuk diselesaikan?)

2. Algoritma Insertion Sort

Seperti pada namanya, algoritma ini menerapkan konsep penyelipan (insertion) seperti pada saat kita mengurutkan kartu remi. Asumsikan kita punya 5 buah kartu remi bergambar hati dengan urutan angka [2, 8, 7, 1, 3 ] yang berada di tangan kanan. Kita ingin mengurutkannya secara ascending. Maka, cara mengurutkannya adalah sebagai berikut (terdiri dari 5 step, banyaknya step sama dengan banyak elemen dalam array):

1. Pindahkan kartu pertama (2 hati) ke tangan kiri {2}, sedangkan 4 kartu lainnya tetap di tangan kanan.
   • kartu di tangan kiri = [2]
   • kartu di tangan kanan [8, 7, 1, 3]
2. Pindahkan kartu kedua (8 hati) ke tangan kiri. Karena 8 > 2, maka posisinya di sebelah kanan kartu 2 hati. Sehingga kartu di tangan kiri sudah terurut untuk 2 elemen.
   • kartu di tangan kiri = [2, 8]
   • kartu di tangan kanan [7, 1, 3]
3. Pindahkan kartu ketiga (7 hati) ke tangan kiri. Periksa nilai 7 dengan nilai terdekatnya di kiri, yaitu 8. Karena 7 < 8, maka 7 berada di sebelah kiri 8. Periksa lagi nilai 7 dengan nilai terdekatnya di kiri, yaitu 2. Karena 7 > 2, maka kartu 7 hati berada di sebelah kanan 2 hati. Dengan kata lain, kartu 7 hati diselipkan di antara kartu 8 hati dan 2 hati.
   • kartu di tangan kiri = [2, 7, 8]
   • kartu di tangan kanan = [1, 3]
4. Pindahkan kartu keempat (1 hati) ke tangan kiri. Periksa nilai 1 dengan nilai terdekatnya di kiri, yaitu 8. Karena 1 < 8, maka 1 hati berada di sebelah kiri 8 hati. Periksa lagi nilai 1 dengan nilai terdekatnya di kiri, yaitu 7. Karena 1 < 7, maka kartu 1 hati berada di sebelah kiri 7 hati. Periksa lagi nilai 1 dengan nilai terdekatnya di kiri, yaitu 2. Karena 1 < 2, maka kartu 1 hati berada di sebelah kiri 2 hati. Karena tidak ada lagi kartu lagi di sebelah kiri, maka selipkan kartu 1 hati di sebelah kiri kartu 2 hati.
   • kartu di tangan kiri = [1, 2, 7, 8]
   • kartu di tangan kanan = [3]
5. Dengan cara yang sama, maka kartu 3 hati akan diselipkan di antara kartu 2 hati dan 7 hati di sebelah kiri.
   • kartu di tangan kiri = [1, 2, 3, 7, 8]
   • kartu di tangan kanan = []
6. Algoritma selesai, didapatkan urutan kartu secara ascending di tangan kiri.

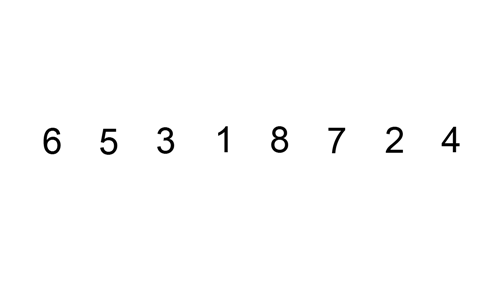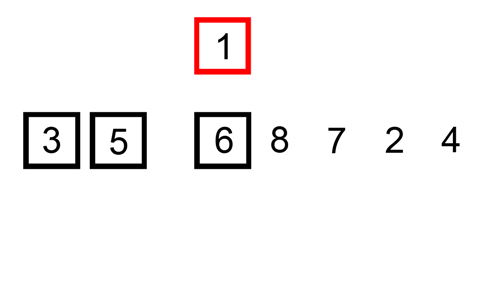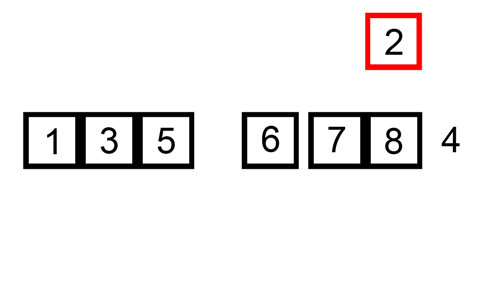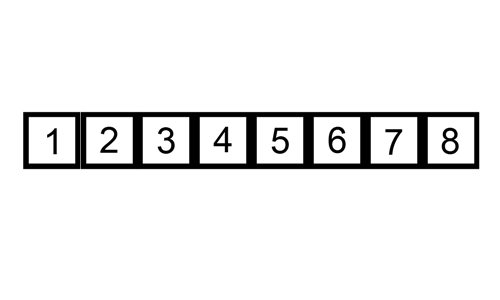
Apabila diimplementasikan dalam bahasa Python, maka kode programnya akan menjadi seperti berikut:

def insertionSort(A):
	for step in range(1, len(A)):
		key = A[step] # simpan nilai key yang akan dipindahkan ke kiri
		j = step - 1 # counter untuk elemen di kiri
		# perulangan selama indeks tidak kurang dari 0
		while j >= 0 and key < A[j]: # kondisi apabila elemen yang akan dipindah kurang dari suatu elemen j yang ada di kiri
			A[j + 1] = A[j] # apabila kondisi benar, geser nilai A[j] ke A[j+1]
			j = j - 1 # mundurkan counter j untuk membandingkan dengan elemen lain
		A[j + 1] = key # jika perulangan berhenti, selipkan nilai key di posisinya yang tepat

A = [9, -3, 5, 2, 6, 8, -6, 1, 3]
insertionSort(A)
print(A)

Algoritma ini memiliki kompleksitas $O(N)$ pada kasus terbaik (elemen sudaha terurut) dan $O(N^2)$ pada kasus rata-rata dan kasus terburuk.

3. Algoritma Quick Sort

3.1 Pendahuluan Quick Sort

Algoritma Quick Sort merupakan salah satu algoritma pengurutan yang memanfaatkan konsep divide and conquer, yaitu konsep untuk menyelesaikan suatu permasalahan dengan cara membagi permasalahan (divide) tersebut menjadi bagian yang lebih kecil, kemudian menyelesaikannya satu-persatu (conquer). Setelah itu, digabung menjadi satu (combine). Selain itu, algoritma ini juga memanfaatkan implementasi rekursif di dalamnya.

Diberikan sebuah array $A[low..high]$ ($low$ merupakan indeks pertama dan $high$ merupakan index terakhir), maka algoritmanya akan berjalan seperti berikut:

• divide : Dilakukan partisi pada array $A[low..high]$ untuk membaginya menjadi dua berdasarkan suatu index $pivot$ (dalam modul ini, yaitu index paling akhir dari $A$), yaitu

  • $A[low..(pivot - 1)]$, dan
  • $A[(pivot+1)..high]$

  sedemikian sehingga semua elemen pada $A[low..(pivot - 1)]$ lebih kecil atau sama dengan $A[pivot]$. Serta nilai $A[pivot]$ lebih kecil atau sama dengan semua elemen pada $A[(pivot+1)..high]$.

• conquer : urutkan dua partisi array $A[low..(pivot - 1)]$ dan $A[(pivot+1)..high]$ menggunakan recursive call.

• combine : Apabila kedua partisi array sudah terurut, maka hentikan proses rekursif karena semua elemen array sudah pasti terurut juga.

Algoritma ini relatif lebih efektif daripada algoritma sorting lainnya karena berjalan dalam kompleksitas waktu $O(N\ log\ N)$ pada kasus rata-rata dan $O(N^2)$ pada kasus terburuk untuk array berukuran $N$ element.

Sebagai gambaran kasar, apabila kita memiliki list sepanjang 100 elemen tak terurut, maka kita dapat mengurutkan list tersebut menggunakan kurang lebih $100 \times log(100)\approx 664$ langkah komputasi pada kasus rata-rata. Pada kasus terburuk (ketika array input sudah terurut, mau tau kenapa? Kita bahas di luar kelas aja wkwk) , kita memerlukan sebanyak $100\times 100=10000$ langkah komputasi.

Sebagai catatan, kompleksitas $O(N\ log\ N)$ merupakan kompleksitas terbaik untuk algoritma sorting pada kasus rata-rata (average case) dibandingkan dengan algoritma sorting lainnya.

3.2 Cara Kerja Algoritma Quick Sort

Dalam implementasinya, terdapat 2 fungsi untuk menjalankan algoritma Quick Sort, yaitu fungsi untuk melakukan dividing (kita beri nama partition) dan fungsi untuk melakukan conquering dan combining (kita beri nama quickSort itu sendiri). Fungsi partition dan quickSort keduanya mengambil 3 parameter, yaitu; A sebagai array, low sebagai index paling awal A, dan high sebagai index paling akhir A.

Untuk melakukan dividing (mencari index pivot untuk mempartisi array), langkah-langkahnya adalah sebagai berikut:

1. Ambil elemen paling kanan sebagai pivot
2. Deklarasikan variabel i sebagai penunjuk dengan nilai low - 1 (sebagai iterator untuk elemen yang lebih besar)
3. Lakukan perulangan menggunakan iterator j dari low hingga high - 1.
4. Pada setiap iterasi, bandingkan A[j] dengan pivot
5. Apabila A[j] lebih kecil atau sama dengan pivot, majukan nilai i sebanyak 1 kemudian tukar nilai A[i] dengan A[j].
6. Setelah perulangan selesai, tukar elemen paling akhir dengan elemen yang ditunjuk oleh i + 1
7. Kembalikan nilai i + 1, yaitu index pivot ketika partisi sudah selesai. Index ini nantinya digunakan untuk menentukan index pivot saat akan melakukan pengurutan pada setiap partisi array A.

Berikut adalah implementasinya menggunakan Python:

def partition(A, low, high):
	pivot = A[high]
	i = low - 1
	for j in range(low, high):
		if A[j] >= pivot: # coba ganti tandanya menjadi <=, apa yang terjadi?
		    i = i + 1
		    A[i], A[j] = A[j], A[i]
	A[i + 1], A[high] = A[high], A[i + 1]
	return i + 1

Untuk melakukan conquering, langkah-langkahnya adalah sebagai berikut:

1. Cari pivot_index yang membagi dua array A dengan semua nilai yang kurang dari atau sama dengan A[pivot_index] berada di sebelah kiri pivot_index dan semua nilai yang lebih dari atau sama dengan A[pivot_index] berada di sebelah kanan pivot_index. Note: nilai ini sudah didapatkan dari fungsi partition.
2. Lakukan recursive call fungsi quickSort untuk partisi di sebelah kiri dari index_pivot
3. Lakukan recursive call fungsi quickSort untuk partisi di sebelah kanan dari index_pivot
4. Apabila, semua elemen sudah terurut, maka recursive call akan berhenti (combining)

Berikut adalah implementasinya menggunakan Python:

def quickSort(A, low, high):
	if low < high:
		pivot_index = partition(A, low, high)
		quickSort(A, low, pivot_index - 1)
		quickSort(A, pivot_index + 1, high)

Untuk mencoba algoritma di atas, ketikkan kode program berikut:

A = [9, -3, 5, 2, 6, 8, -6, 1, 3]
quickSort(A, 0, len(A) - 1)
print(A)

List di atas diproses seperti yang digambarkan oleh gambar di bawah ini:

4. Algoritma Merge Sort

Seperti halnya algoritma Quick Sort, algoritma Merge Sort juga menerapkan konsep divide and conquer serta konsep rekursi namun dengan cara kerja yang berbeda.

Diberikan sebuah array $A$ berukuran $n$ element, maka algoritmanya akan berjalan seperti berikur:

• divide : bagi array $A$ berukuran $n$ elemen menjadi dua subarray dengan panjang masing-masing $n/2$.
• conquer : urutkan masing-masing subarray secara rekursif hingga mencapai base case. Base case dari rekursif ini adalah ketika subarray hanya memiliki 1 elemen saja.
• combine : Ketika setiap langkah conquer sudah mencapai base case, maka hasil dari setiap recursive call digabung hingga menghasilkan array baru $A$ berukuran $n$ yang sudah terurut:

Untuk lebih mendapatkan idenya, perhatikan gambar di bawah ini. Sebagai catatan, angka berwarna hijau menandakan urutan langkah yang dieksekusi.

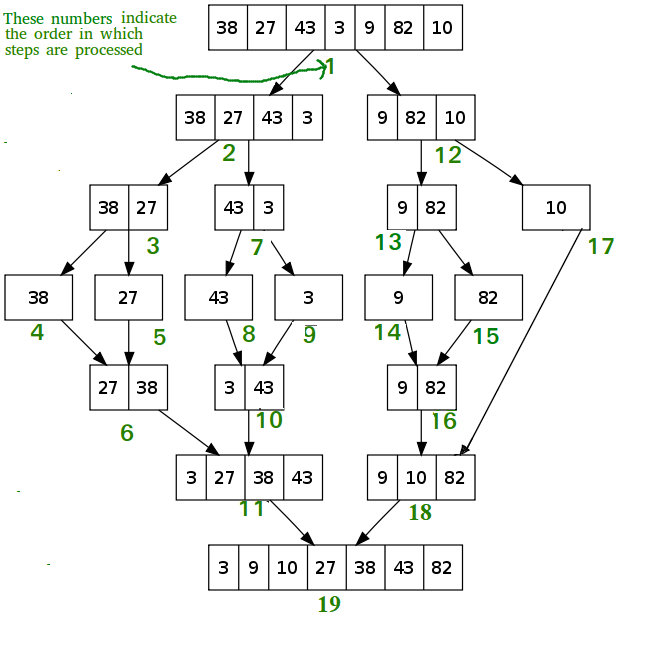
Dalam implementasinya menggunakan bahasa Python, perhatikan kode program berikut:

def mergeSort(A):
	if len(A) > 1:
		mid = int(len(A)/2) # cari pembagi array (median index)
		L = A[:mid] # inisiasikan subarray dari 0 hingga mid - 1
		R = A[mid:] # inisiasikan subarray dari mid hingga len(A) - 1
		mergeSort(L) # urutkan subarray di kiri dengan recursive call
		mergeSort(R) # urutkan subarray di kiri dengan recursive call
		
		i = j = k = 0
		# proses sorting setiap subarray
		while i < len(L) and j < len(R):
			if L[i] <= R[j]:
				A[k] = L[i]
				i = i + 1
			else:
				A[k] = R[j]
				j = j + 1
			k = k + 1
	
		# proses merging dari subarray kiri dan kanan ke array A
		while i < len(L):
			A[k] = L[i]
			i = i + 1
			k = k + 1
		while j < len(R):
			A[k] = R[j]
			j = j + 1
			k = k + 1

A = [9, -3, 5, 2, 6, 8, -6, 1, 3]
mergeSort(A)
print(A)

Algoritma ini berjalan dalam kompleksitas $O(N)$ pada kasus terbaik dan $O(N\ log\ N)$ pada kasus rata-rata dan terburuk. Walaupun relatif lebih efisien secara waktu komputasi daripada Quick Sort, algoritma ini lebih boros memory karena terus-menerus mengalokasikan memory untuk pembuatan subarray baru saat recursive call.

---

Selection Sort

Selection Sort adalah salah satu algoritma pengurutan sederhana yang bekerja dengan cara mencari elemen terkecil dari array dan menukarnya dengan elemen pertama. Kemudian, mencari elemen terkecil kedua dari array dan menukarnya dengan elemen kedua, dan begitu seterusnya hingga seluruh array terurut.

Cara Kerja

1. Pencarian Elemen Terkecil: Pertama, algoritma mencari elemen terkecil dari array.

2. Menukar dengan Elemen Pertama: Setelah menemukan elemen terkecil, algoritma menukarnya dengan elemen pertama.

3. Pencarian Elemen Terkecil Kedua: Kemudian, algoritma mencari elemen terkecil kedua dari array, yang dimulai dari elemen kedua hingga elemen terakhir.

4. Menukar dengan Elemen Kedua: Setelah menemukan elemen terkecil kedua, algoritma menukarnya dengan elemen kedua.

5. Pola Berlanjut: Proses ini berlanjut hingga seluruh array terurut.

Kelebihan

• Sederhana untuk diimplementasikan.
• Membutuhkan sedikit penulisan kode.

Kekurangan

• Tidak efisien untuk array besar karena memiliki kompleksitas waktu O(n^2).
• Tidak efisien untuk array yang hampir terurut karena akan melakukan pertukaran pada setiap langkahnya.

Implementasi Python

def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        # Mencari indeks elemen terkecil yang belum diurutkan
        min_index = i
        for j in range(i + 1, n):
            if arr[j] < arr[min_index]:
                min_index = j
        
        # Menukar elemen terkecil dengan elemen pertama yang belum diurutkan
        arr[i], arr[min_index] = arr[min_index], arr[i]
    
    return arr

# Contoh penggunaan
data = [64, 25, 12, 22, 11]
print("Unsorted Array:", data)
sorted_data = selection_sort(data)
print("Sorted Array:", sorted_data)

Kompleksitas Waktu

• Rata-rata: O(n^2)
• Terburuk: O(n^2)

Kompleksitas Ruang

• O(1) - In-place sorting, tidak memerlukan ruang tambahan.