Modul 11 : Graph - fzl-22/modul-alstrukdat-informatika GitHub Wiki

Non Linear Data Structure

Struktur data non linear merupakan struktur data yang tidak tersusun secara barisan atau linear sehingga struktur data ini berbeda dengan array dan linked list yang telah kita pelajari sebelumnya. Penyusunan data dalam struktur data non linear dilakukan dengan lebih kompleks seperti penyusunan hirarki dan keterhubungan antar element yang lebih banyak. Adapun jenis dari struktur data non linear adalah tree dan graph yang mana akan kita bahas pada pertemuan hari ini.

image

Definisi Graph

Graph adalah salah satu jenis dari struktur data non linear. Adapun terdapat beberapa istilah atau terminologi yang perlu dipahami mengenai graph yaitu:

  1. Vertex/Simpul atau pada linked list biasa disebut node yang mana merupakan element atau object yang menyimpan data dan dapat saling terhubung satu sama lain.
  2. Edge/Sisi, koneksi atau hubungan antar dua vertex dalam graph.
  3. Directed Graph. jenis graph yang memiliki arah dalam edgenya.
  4. Underected Graph, jenis graph yang tidak memiliki arah dalam edgenya.

Untuk lebih memahami perhatikan gambar berikut:

image

Dapat dilihat perbedaan edge atau simpul dari kedua contoh graph di atas. Pada gambar sebelah kiri menunjukkan panah yang mana mengartikan edge dari vertex ke vertexnnya tetapi pada vertex sebelah kanan edge hanya berupa garis biasa yang menunjukkan bahwa tidak ada arah pada edgenya. Maksud dari arah disini adalah perpindahan vertex sebagai contoh:

  • A -> B : Artinya dari vertex A dapat menelusuri atau mengakses ke vertex B tetapi tidak sebaliknya.
  • A - B : Artinya dari vertex A dapat menelusuri atau mengakses ke vertex B dan sebaliknya.

Lalu bagaimana cara mengimplementasikan struktur data graph ke dalam bahasa pemograman bahasa C? Jawabannya adalah ada beberapa metode tetapi pada pembelajaran kali ini hanya akan dibahas dua metode yaitu Adjacency List dan Adjacency Graph.

Adjacency Matrix

Adjacency Matrix merupakan metode pengimplementasian graph menggunakan matrix 2D dengan ukuran n x n. Setiap indeks mewakili satu hubungan atau satu edge antar vertex. Perhatikan contoh berikut:

image

Pada gambar di atas dapat dilihat bahwa terdapat sebuah tabel matrix berukuran n x n yang mana n adalah jumlah vertex dari graph. Kemudian perhatikan pada setiap index terdapat angka 0 yang mengartikan bahwa pada index tersebut tidak terdapat keterhubungan atau edge seperti index[1][0] yang bernilai 0 karena tidak ada edge yang mengarah dari vertex 1 ke vertex 0. Namun, coba perhatikan pada index[0][1] bernilai 1 yang menandakan terdapat edge antar vertex tersebut.

Adapun untuk implementasinya perhatikan contoh berikut:

Mendeklarasikan Struct Graph

struct Graph
{
    int numVertices;
    int **adjMatrix;
};

Graph yang akan kita deklarasikan memiliki dua data yang penting untuk disimpan yaitu numVertices yang menandkan jumlah vertex yang disimpan dan **adjMatrix adalah array2D yang akan menyimpan indeks matrix 2D sehingga diperlukan penggunaan double pointer.

Mendeklarasikan Graph

// Fungsi untuk membuat graph dengan vertex awal
struct Graph *createGraph()
{
    struct Graph *graph = (struct Graph *)malloc(sizeof(struct Graph));
    graph->numVertices = 0;
    graph->adjMatrix = NULL;
    return graph;
}

Pada kode di atas dilakukan pembuatan awal graph sehingga tidak memiliki node. Untuk itu pada numVertices diberikan value 0 karena tidak terdapat vartives pada graph tersebut begitu pula dengan adjMatrix yang bernilai NULL.

Menambahkan Vertex

// Fungsi untuk menambahkan vertex baru ke dalam graph
void addVertex(struct Graph *graph)
{
    int newVertices = graph->numVertices + 1;

    // Alokasi memori untuk adjacency matrix baru
    graph->adjMatrix = (int **)realloc(graph->adjMatrix, newVertices * sizeof(int *));
    graph->adjMatrix[newVertices - 1] = (int *)malloc(newVertices * sizeof(int));

    int i;
    for (i = 0; i < newVertices; i++)
    {
        graph->adjMatrix[i] = (int *)realloc(graph->adjMatrix[i], newVertices * sizeof(int));
        graph->adjMatrix[i][newVertices - 1] = 0;
        graph->adjMatrix[newVertices - 1][i] = 0;
    }

    graph->numVertices++;
}

Kode di atas adalah fungsi untuk menambahkan vertex pada graph yang telah dideklarasikan. Dapat dilihat jumlah dari numVertices dilakukan penambahan dengan 1 di akhir fungsi. Kemudian, dilakukan alokasi memori menggunakan realloc yaitu mengalokasikan memori baru dengan ukuran baru. Fungsi realloc menerima dua parameter yang mana dapat dilihat pada kode di atas yaitu (graph->adjMatrix) yaitu memori awal dari alokasi data lama ke data baru dan newVertices * sizeof(int)) untuk mendeklarasikan ukuran dari memori yang dialokasikan. Kemudian pada vertices baru dengan enggunakan graph->adjMatrix[newVertices - 1] dilakukan alokasi memori sejumlah banyak vertices yang baru. Lalu bagaimana dengan vertices yang lama? Pada kode selanjutnya dilakukan looping kepada seluruh vertices yang ada untuk memperbarui jumlah kolom yang per vertices muat dan dilanjutkan dengan pengalokasian nilai pada vertices baru dengan nilai 0 karena belum memiliki edge.

Operasi Menambahkan Edge

// Fungsi untuk menambahkan sisi antara dua simpul dalam graph
void addEdge(struct Graph *graph, int src, int dest)
{
    if (src >= 0 && src < graph->numVertices && dest >= 0 && dest < graph->numVertices)
    {
        graph->adjMatrix[src][dest] = 1;
        graph->adjMatrix[dest][src] = 1;
    }
    else
    {
        printf("Invalid vertex!\n");
    }
}

Untuk menambahkan edge perlu dipastikan bahwa vertices dari src atau asal dan dst atau tujuannya adalah. Oleh karena itu dilakukan pengecekan terlebih dahulu apakah vertex yang akan digunakan valid atau tidak. Jika vertex telah dipastikan aman maka akses index vertex tersebut dan ubah nilainya menjadi 1.

Menampilkan Graph

// Fungsi untuk mencetak adjacency matrix
void printGraph(struct Graph *graph)
{
    int i, j;
    for (i = 0; i < graph->numVertices; i++)
    {
        for (j = 0; j < graph->numVertices; j++)
        {
            printf("%d ", graph->adjMatrix[i][j]);
        }
        printf("\n");
    }
    printf("\n");
}

Untuk menampilkan graph maka caranya sama saja dengan menampilkan array 2D yaitu menggunakan nested loop yang masing - masing dari 0 hingga jumlah vertex pada graph.

Implementasi Lengkap

Adapun berikut kode full dari implementasi graph menggunakan metode Adjacency Matrix:

#include <stdio.h>
#include <stdlib.h>

struct Graph
{
    int numVertices;
    int **adjMatrix;
};

// Fungsi untuk membuat graph dengan vertex awal
struct Graph *createGraph()
{
    struct Graph *graph = (struct Graph *)malloc(sizeof(struct Graph));
    graph->numVertices = 0;
    graph->adjMatrix = NULL;
    return graph;
}

// Fungsi untuk menambahkan vertex baru ke dalam graph
void addVertex(struct Graph *graph)
{
    int newVertices = graph->numVertices + 1;

    // Alokasi memori untuk adjacency matrix baru
    graph->adjMatrix = (int **)realloc(graph->adjMatrix, newVertices * sizeof(int *));
    graph->adjMatrix[newVertices - 1] = (int *)malloc(newVertices * sizeof(int));

    int i;
    for (i = 0; i < newVertices; i++)
    {
        graph->adjMatrix[i] = (int *)realloc(graph->adjMatrix[i], newVertices * sizeof(int));
        graph->adjMatrix[i][newVertices - 1] = 0;
        graph->adjMatrix[newVertices - 1][i] = 0;
    }

    graph->numVertices++;
}

// Fungsi untuk menambahkan sisi antara dua simpul dalam graph
void addEdge(struct Graph *graph, int src, int dest)
{
    if (src >= 0 && src < graph->numVertices && dest >= 0 && dest < graph->numVertices)
    {
        graph->adjMatrix[src][dest] = 1;
        graph->adjMatrix[dest][src] = 1;
    }
    else
    {
        printf("Invalid vertex!\n");
    }
}

// Fungsi untuk mencetak adjacency matrix
void printGraph(struct Graph *graph)
{
    int i, j;
    for (i = 0; i < graph->numVertices; i++)
    {
        for (j = 0; j < graph->numVertices; j++)
        {
            printf("%d ", graph->adjMatrix[i][j]);
        }
        printf("\n");
    }
    printf("\n");
}

// Fungsi utama
int main()
{
    struct Graph *graph = createGraph();
    printGraph(graph);
    int pilihan;
    do
    {
        printGraph(graph);
        printf("Menu\n1.Buat Vertex Baru\n2.Buat Edge\nMasukkan pilihan : ");
        scanf("%d", &pilihan);
        if (pilihan == 1)
        {
            addVertex(graph);
        }
        else if (pilihan == 2)
        {
            int src, dst;
            scanf("%d %d", &src, &dst);
            addEdge(graph, src, dst);
        }
        system("cls");

    } while (pilihan != 0);
}

Adjacency List

Adjacency list representasi dari graph yang memanfaatkan linked list. Ide dari perepresentasian dengan menggunakan Adjacency List adalah dengan hanya menyimpan daftar dari vertex-vertex lain yang memiliki edge yang terhubung dengan suatu vertex. Dalam hal ini, secara mudah dapat dikatakan bahwa adjacency list merepresentasikan graph sebagai array dari beberapa linked list.

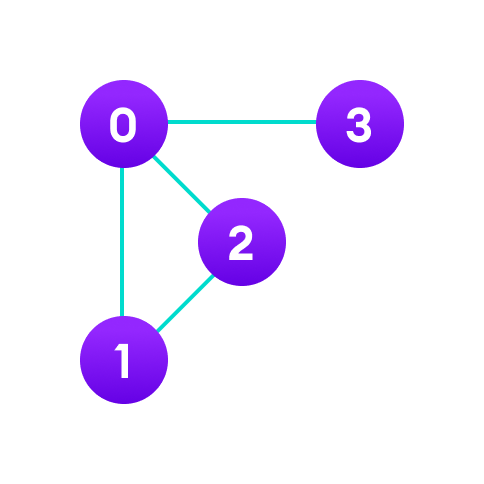
Sebagai contoh, terdapat graph berikut:

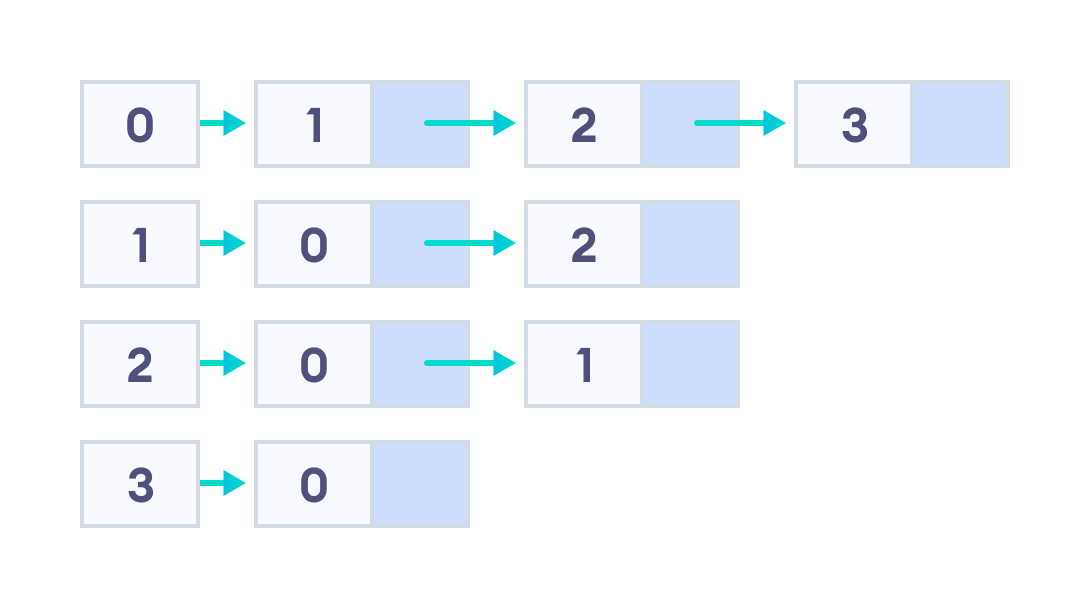
Maka, graph di atas dapat direpresentasikan menjadi linked list seperti gambar di bawah ini:

Kenapa harus menggunakan adjacency list? Karena masalah utama dari penggunaan adjacency matrix adalah penggunaan memory yang menghabiskan sebanyak $V^2$ memory untuk graf dengan banyak vertex sebanyak $V$, sehingga tidak memungkinkan untuk graf dengan ukuran besar.

Struktur Adjacency List

// Node yang merepresentasikan edge di adjacency list
typedef struct Node {
    int dest;
    struct Node* next;
} Node;

// Structure graph
typedef struct Graph {
    int numVertices;
    Node** adjList;
} Graph;

Membuat Node Baru

Node* createNode(int dest) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->dest = dest;
    newNode->next = NULL;
    return newNode;
}

Membuat Graph (Fixed Vertex)

Graph* createGraph(int numVertices) {
    Graph* graph = (Graph*)malloc(sizeof(Graph));
    graph->numVertices = numVertices;

    // Membuat array dari adjacency list
    graph->adjList = (Node**)malloc(numVertices * sizeof(Node*));

    // Isi nilai setiap adjacency list dengan NULL 
    for (int i = 0; i < numVertices; ++i) {
        graph->adjList[i] = NULL;
    }

    return graph;
}

Menambahkan Edge pada Undirected Graph

void addEdge(Graph* graph, int src, int dest) {
    // Tambahkan edge dari vertex source ke vertex destination
    Node* newNode = createNode(dest);
    newNode->next = graph->adjList[src];
    graph->adjList[src] = newNode;

    // Tambahkan edge dari vertex destination ke vertex source
    newNode = createNode(src);
    newNode->next = graph->adjList[dest];
    graph->adjList[dest] = newNode;
}

Menampilkan Graph (Berdasarkan Vertex dan Vertex Tetangganya)

void printGraph(Graph* graph) {
    for (int v = 0; v < graph->numVertices; ++v) {
        Node* temp = graph->adjList[v];
        printf("Adjacency list of vertex %d\n", v);
        while (temp) {
            printf("%d -> ", temp->dest);
            temp = temp->next;
        }
        printf("NULL\n");
    }
}

Membebaskan Memory dari Graph yang Sudah Tidak Terpakai

void destroyGraph(Graph* graph) {
    if (graph) {
        if (graph->adjList) {
            for (int i = 0; i < graph->numVertices; ++i) {
                Node* temp = graph->adjList[i];
                while (temp) {
                    Node* prev = temp;
                    temp = temp->next;
                    free(prev);
                }
            }
            free(graph->adjList);
        }
        free(graph);
    }
}

Implementasi Lengkap

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int dest;
    struct Node* next;
} Node;

typedef struct Graph {
    int numVertices;
    Node** adjList;
} Graph;

Node* createNode(int dest) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->dest = dest;
    newNode->next = NULL;
    return newNode;
}

Graph* createGraph(int numVertices) {
    Graph* graph = (Graph*)malloc(sizeof(Graph));
    graph->numVertices = numVertices;

    // Create an array of adjacency lists
    graph->adjList = (Node**)malloc(numVertices * sizeof(Node*));

    // Initialize each adjacency list as empty
    for (int i = 0; i < numVertices; ++i) {
        graph->adjList[i] = NULL;
    }

    return graph;
}

void addEdge(Graph* graph, int src, int dest) {
    // Add an edge from src to dest
    Node* newNode = createNode(dest);
    newNode->next = graph->adjList[src];
    graph->adjList[src] = newNode;

    // Add an edge from dest to src
    newNode = createNode(src);
    newNode->next = graph->adjList[dest];
    graph->adjList[dest] = newNode;
}

void printGraph(Graph* graph) {
    for (int v = 0; v < graph->numVertices; ++v) {
        Node* temp = graph->adjList[v];
        printf("Adjacency list of vertex %d\n", v);
        while (temp) {
            printf("%d -> ", temp->dest);
            temp = temp->next;
        }
        printf("NULL\n");
    }
}

void destroyGraph(Graph* graph) {
    if (graph) {
        if (graph->adjList) {
            for (int i = 0; i < graph->numVertices; ++i) {
                Node* temp = graph->adjList[i];
                while (temp) {
                    Node* prev = temp;
                    temp = temp->next;
                    free(prev);
                }
            }
            free(graph->adjList);
        }
        free(graph);
    }
}

int main() {
    // Membuat graph dengan 5 vertex
    Graph* graph = createGraph(5);

    // Menambahkan edge
    addEdge(graph, 0, 1);
    addEdge(graph, 0, 4);
    addEdge(graph, 1, 2);
    addEdge(graph, 1, 3);
    addEdge(graph, 1, 4);
    addEdge(graph, 2, 3);
    addEdge(graph, 3, 4);

    // Menampilkan graph
    printGraph(graph);

    // Membebaskan memory dari graph
    destroyGraph(graph);
    
    return 0;
}

🟣Asisten Praktikum Algoritma Struktur Data Informatika 2023🟣

⚠️ **GitHub.com Fallback** ⚠️