Modul 10. Algoritma Rekursif - fzl-22/modul-alstrukdat-informatika GitHub Wiki
Modul Praktikum Algoritma Rekursif
Tujuan
- Memahami konsep dan cara kerja algoritma rekursif
- Mampu menulis dan menjalankan program yang menggunakan algoritma rekursif
- Mampu menganalisis kompleksitas waktu dan ruang dari algoritma rekursif
Materi
Pengertian Rekursif
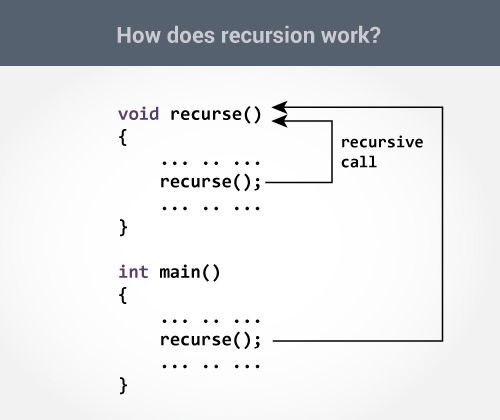
Rekursif adalah suatu proses yang mengandung pemanggilan diri sendiri secara berulang-ulang. Dalam konteks pemrograman, rekursif adalah suatu fungsi yang memanggil dirinya sendiri dalam definisinya.
Contoh:
// Fungsi untuk menghitung faktorial dari n secara rekursif
int faktorial(int n) {
// Basis: jika n = 0 atau n = 1, maka faktorial(n) = 1
if (n == 0 || n == 1) {
return 1;
}
// Rekurens: jika n > 1, maka faktorial(n) = n * faktorial(n-1)
else {
return n * faktorial(n-1);
}
}
Keuntungan dan Kerugian Rekursif
Keuntungan menggunakan rekursif adalah:
- Kode program menjadi lebih singkat, sederhana, dan elegan
- Memudahkan penyelesaian masalah yang bersifat rekursif, seperti pencarian biner, permutasi, kombinasi, dll.
- Memungkinkan penggunaan struktur data yang bersifat rekursif, seperti pohon, graf, dll.
Kerugian menggunakan rekursif adalah:
- Membutuhkan lebih banyak memori untuk menyimpan informasi pemanggilan fungsi
- Membutuhkan lebih banyak waktu untuk mengeksekusi pemanggilan fungsi
- Berpotensi menyebabkan stack overflow jika terlalu banyak pemanggilan fungsi
Kompleksitas Waktu dan Ruang Rekursif
Kompleksitas waktu dari suatu algoritma rekursif dapat dihitung dengan menggunakan persamaan rekurens. Persamaan rekurens adalah suatu persamaan yang menghubungkan nilai fungsi pada suatu kasus dengan nilai fungsi pada kasus-kasus sebelumnya. Contoh:
// Fungsi untuk menghitung bilangan Fibonacci ke-n secara rekursif
int fibonacci(int n) {
// Basis: jika n = 0, maka fibonacci(n) = 0; jika n = 1, maka fibonacci(n) = 1
if (n == 0) {
return 0;
}
else if (n == 1) {
return 1;
}
// Rekurens: jika n > 1, maka fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)
else {
return fibonacci(n-1) + fibonacci(n-2);
}
}
Persamaan rekurens untuk fungsi fibonacci adalah:

Dimana $c_1$, $c_2$, dan $c_3$ adalah konstanta yang merepresentasikan waktu yang dibutuhkan untuk mengevaluasi kondisi, mengembalikan nilai, dan melakukan operasi penjumlahan. Untuk menyelesaikan persamaan rekurens ini, kita dapat menggunakan metode substitusi, iterasi, atau karakteristik. Salah satu cara yang mudah adalah dengan menggunakan metode iterasi. Metode iterasi adalah metode yang menggantikan nilai $T(n)$ dengan nilai-nilai sebelumnya sampai diperoleh pola umum. Contoh: $$T(n) = T(n-1) + T(n-2) + c_3$$ $$T(n) = (T(n-2) + T(n-3) + c_3) + T(n-2) + c_3$$ $$T(n) = (T(n-3) + T(n-4) + c_3) + 2T(n-2) + 2c_3$$ $$T(n) = (T(n-4) + T(n-5) + c_3) + 3T(n-2) + 3c_3$$ $$...$$ $$T(n) = T(0) + T(1) + (n-1)c_3 + \sum_{i=0}^{n-2} i T(i)$$ Dari pola umum ini, kita dapat melihat bahwa $T(n)$ tumbuh secara eksponensial seiring dengan bertambahnya $n$. Oleh karena itu, kompleksitas waktu dari fungsi fibonacci adalah $O(2^n)$. Kompleksitas ruang dari suatu algoritma rekursif dapat dihitung dengan menghitung jumlah pemanggilan fungsi yang disimpan dalam stack. Jumlah pemanggilan fungsi ini bergantung pada kedalaman rekursi, yaitu jumlah pemanggilan fungsi yang belum selesai. Contoh:
// Fungsi untuk menghitung faktorial dari n secara rekursif
int faktorial(int n) {
// Basis: jika n = 0 atau n = 1, maka faktorial(n) = 1
if (n == 0 || n == 1) {
return 1;
}
// Rekurens: jika n > 1, maka faktorial(n) = n * faktorial(n-1)
else {
return n * faktorial(n-1);
}
}
Jika kita memanggil fungsi faktorial(5), maka stack akan berisi:
Stack
faktorial(5)
faktorial(4)
faktorial(3)
faktorial(2)
faktorial(1)
Kedalaman rekursi dari fungsi faktorial adalah $n$, sehingga kompleksitas ruang dari fungsi faktorial adalah $O(n)$.
Latihan
Soal 1
Tulislah program dalam bahasa C yang menggunakan algoritma rekursif untuk menghitung nilai dari $x^y$, dimana $x$ dan $y$ adalah bilangan bulat positif yang diinputkan oleh user. Asumsikan bahwa $x^0 = 1$.
Kumpulkan di sini!
Referensi