Quick sort merupakan salah satu jenis algoritma sorting dalam kelompok comparasion sort atau melakukan perbandingan nilai dua element untuk menentukkan posisi yang tepat dari element tersebut. Selain itu algoritma quick sort juga termasuk ke dalam Devide & Conquer Algorithm yaitu algoritma yang menyelesaikan suatu permasalahan dengan cara membagi permasalahan tersebut menjadi bagian-bagian yang lebih kecil dan menyelesaikannya per bagian kemudian digabung menjadi satu. Dalam melakukan quick sort terdapat implementasi recursive di dalamnya, sehingga diperlukan pemahaman recursive untuk melakukan Quick Sort

Recursive merupakan suatu kondisi dimana sebuah fungsi memanggil dirinya sendiri. Dengan kondisi tersebut, maka pemanggilan fungsi akan terlihat seperti sebuah looping karena suatu fungsi akan melakukan statement yang terdapat di dirinya sendiri secara berulang kali. Karena nampak seperti looping, maka dibutuhkan sebuah kondisi untuk menghentikan perulangan tersebut yang mana disebut dengan base case. Jika sebuah fungsi menemukan base case maka recursive akan berhenti.

Untuk melakukan recursive maka dapat dituliskan sebagai berikut :

#include <stdio.h>

int rekursif(int x){
    printf("%d", x);
    if (x > 0){ // --> Recursive Case (kondisi yang apabila bernilai true akan memanggil dirinya sendiri)
        return rekursif(x - 1); 
    }else{ // --> Base Case (kondisi yang apabila bernilai true akan mengentikan rekursi)
        return;
    }
}

int main(){
    int y = rekursif(10);
}

Output :

10 9 8 7 6 5 4 3 2 1 0

Untuk lebih memahami recursive maka akan lebih mudah jika divisualisasikan melalui struktur data stack, hal tersebut dikarenakan recursive merupakan salah satu implementasi dari sruktur data stack. Visualisasi struktur data stack pada recursive dapat dilihat pada gambar di bawah ini :

Pada gambar kotak di atas merupakan kondisi ketika fungsi memanggil dirinya sendiri dan gambar kotak di bawah merupakan kondisi ketika base case telah ditemukan dan fungsi mulai melakukan return value.

Pemahaman recursive akan mempermudah kita dalam melakukan implementasi algoritma quick sort. Jika pada algoritma-algoritma sorting sebelumnya dilakukan comparasion sebuah nilai dengan nilai setelahnya, maka pada Quick Sort akan sedikit berbeda. Pada Quick Sort dipilih sebuah nilai yang disebut pivot yang akan dijadikan patokan pengurutan dan dijadikan nilai pembanding. Nilai pivot ini diambil dari salah satu nilai dalam sebuah baris nilai yang akan diurutkan, dapat diambil dari nilai awal baris, tengah baris, atau akhir baris. Namun, setiap letak nilai yang diambil memiliki algoritma yang berbeda-beda, sehingga algoritma quick sort untuk nilai pivot tengah akan berbeda dengan ketika mengambil nilai pivot awal.

Selain itu telah dijelaskan di awal bahwa Quick Sort merupakan devide & conquare algorithm yang mana dapat dilihat pada gambar di atas algotitma quick sort melakukan pemecahan partisi atau baris data yang kemudian tiap-tiap pecahan baris data tersebut dilakukan sorting menggunakan algoritma quick sort kembali. Pemecahan tersebut dilakukan secara berulang-ulang hingga semua data dipastikan urut.

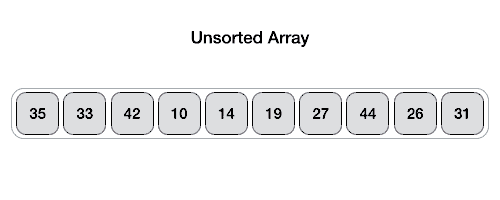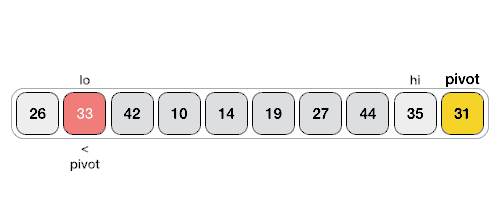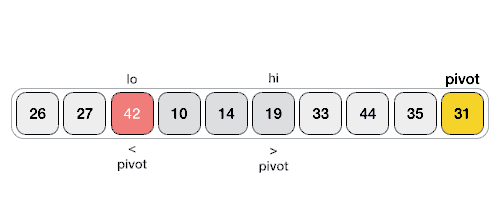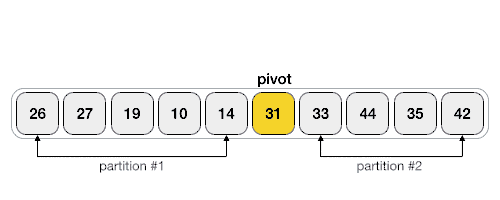
Visualisasi dari berjalannya algoritma quick sort dapat dilihat pada gambar di bawah ini :

Jika dilihat pada visualisasi di atas dapat diperhatikan bahwa bahwa algoritma quick sort melakukan pengurutan sebagai berikut :

1. Menentukkan nilai pivot
2. Mencari nilai yang lebih besar dari pivot dari baris awal - akhir
3. Mencari nilai yang lebih kecil dari pivot dari baris akhir - awal
4. Melakukan penukaran nilai yang lebih besar dengan nilai yang lebih kecil dari pivot
5. Jika pencarian nilai lebih kecil dan nilai yang lebih besar bertemu maka yang dilakukan adalah menukar lokasi terakhir pencarian nilai yang lebih kecil dengan nilai pivot
6. Membagi baris tersebut menajadi 2 partisi dengan pembagian index pivot - 1 dan index pivot + 1
7. Kembali ke nomor 1 dan berhenti ketika semua data telah tersorting

WARNING!!!! algoritma di atas hanya berlaku ketika kita memilih pivot pada index awal dan index akhir

Berikut merupakan kode program quick sort dengan pivot pada index akhir :

#include <stdio.h>

int quicksort(int x, int y, int z[])
{

    int start, finish, pivot, temp, cek;
    start = x;
    finish = y;
    pivot = y;

    if (start <= finish)
    {
        while (start < finish)
        {
            while (z[start] <= z[pivot]) // --> Mencari nilai yang lebih besar dari pivot
            {
                start++;
            }
            while (z[finish] > z[pivot]) // --> Mencari nilai yang lebih kecil dari pivot
            {
                finish--;
            }
            if (start < finish) // --> Memastikan bahwa pencarian nilai lebih besar dan lebih kecil belum saling bertemu
            {
                // Menukar nilai yang lebih besar dengan pivot dengan nilai yang lebih kecil dari pivot
                temp = z[finish];
                z[finish] = z[start];
                z[start] = temp;
            }
        }
        // Menukar nilai pivot dengan nilai pencarian nilai lebih kecil
        temp = z[pivot]; 
        z[pivot] = z[finish];
        z[finish] = temp;

        quicksort(x, finish - 1, z);
        quicksort(finish + 1, y, z);
    }
    else
    {
        return;
    }
}

void tampil(int x[], int y)
{
    for (int a = 0; a < y; a++)
    {
        printf("%d ", x[a]);
    }
    puts(" ");
}

int main()
{

    int angka[] = {3, 5, 1, 4, 2, 6, 10, 7, 9, 8};
    int jumlah = sizeof(angka) / sizeof(angka[0]);

    printf("ARRAY SEBELUM SORTING : ");
    tampil(angka, jumlah);

    quicksort(0, jumlah - 1, &angka);

    printf("ARRAY SESUDAH SORTING : ");
    tampil(angka, jumlah);
}

Output :

ARRAY SEBELUM SORTING : 3 5 1 4 2 6 10 7 9 8  
ARRAY SESUDAH SORTING : 1 2 3 4 5 6 7 8 9 10 

Buatlah algoritma untuk mencari nilai tertinggi dari suatu array berukuran $N$ dengan memanfaatkan algoritma quick sort. Setelah itu, buatlah juga algoritma yang memanfaatkan algoritma linear search (binary search jika memungkinkan) untuk menyelesaikan persoalan yang sama. Kedua algoritma tersebut wajib dibuat dalam dua fungsi/prosedur yang berbeda. Selain itu, dilarang mengakali algoritma dengan memodifikasi fungsi main (kecuali input dan output). Terakhir, presentasikan program dan tentukan algoritma mana yang lebih efisien serta mengapa algoritma yang satu lebih efisien daripada algoritma lainnya dengan argumenmu sendiri.

Note: algoritma yang ditulis dalam fungsi/prosedur tidak boleh mengubah nilai dan urutan dari array yang berada di fungsi main.

Baris pertama berisi bilangan bulat $N$, dilanjutkan dengan sebanyak $N$-baris berisi bilangan bulat yang merupakan elemen-elemen dari array.

Terdiri dari satu baris saja, yaitu nilai tertinggi yang terdapat dalam array.

10
4
3
5
9
2
8
7
3
4
6

9