1. Algoritma Searching

Dalam dunia pemrograman terdapat sebuah permasalahan yang sering ditemui yaitu permasalahan pencarian data. Untuk menyelesaikan permasalahan tersebut maka dibuatlah Searching Algorithm yaitu algoritma yang digunakan untuk mencari satu atau banyak data di antara sekelompok data.

Pada python sendiri terdapat operator yang dapat digunakan untuk mencari data pada suatu list yaitu operator in yang mana penerapannya adalah sebagai berikut:

angka = [1,2,3,4,5]
print(1 in angka)

Output:

True

Pada cara di atas, kita telah dipermudah untuk mencari data dengan menggunakan in operator. Di belakang in operator terdapat sebuah algoritma yang berjalan untuk mencari data yang diinginkan yang mana menggunakan Linear atau Sequential Search.

Terkadang kita membutuhkan suatu metode pencarian yang lebih cepat dari in operator. Untuk menjawab kebutuhan tersebut maka terdapat beberapa jenis Searching Algorithm yang dapat digunakan. Pada pembahasan kali ini jenis dari Searching Algorithm yang akan dibahas adalah Linear Search dan Binary Search

1.1 Linear Search

Linear Search merupakan sebuah algoritma pencarian yang melakukan pencarian dengan melakukan pencocokan setiap element dari awal hingga ditemukan element yang dicari. Jika kita ilustrasikan sebuah buku maka dan data adalah halaman yang ingin kita cari, maka Linear Searching adalah metode untuk menemukan halaman tersebut dengan membuka satu persatu halaman buku tersebut. Berikut merupakan ilustrasi dari berjalannya Linear Searching.

Pada ilustrasi di atas Linear Searching akan melakukan pencarian pada setiap data pada baris data dari awal hingga akhir. Dengan metode seperti itu maka Linear Searching setidaknya membutuhkan N langkah untuk case terburuk dan 1 langkah untuk case terbaik.

Adapun untuk implementasi kode pemograman dari Linear Searching adalah sebagai berikut:

angka = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

cari = int(input())
ketemu = -1
for i in angka:
    if (i == cari):
        ketemu = 1

if (ketemu == 1):
    print("ketemu")
else:
    print("gak ketemu")

1.2 Binary Search

Algoritma Searching lainnya adalah Binary Search, hal utama yang perlu diketahui adalah algoritma ini hanya berlaku untuk data yang telah terurut. Namun, meskipun begitu algoritma Binary Search memiliki kompleksitas yang lebih tinggi daripada Linear Search yaitu log(n) complexity. Hal tersebut dikarenakan cara kerja dari binary search yang sebagai berikut:

1. Algoritma akan langsung melakukan pencarian pada data tengah (setengah panjang data).
2. Pencarian dilakukan dengan melakukan komparasi apakah data yang dicari lebih besar atau lebih kecil dari data yang diakses.
3. Jika lebih kecil maka akan dilakukan pencarian pada bagian tengah data yang lebih kecil dari data sebelumnya dan sebaliknya.
4. Dilakukan komparasi kembali dan langkah nomor 3 dilakukan berulang kali hingga data ditemukan.
5. Jika data tidak ditemukan maka area pencarian nanti akan tersisa satu data saja dan jika data yang tersisa itu tidak sesuai maka dapat disimpulkan bahwa data tidak ditemukan.

Adapun berikut ilustrasi dari Binary Search:

Berikut kode program implementasi dari Binary Search:

def binary_search(arr, x):
    low = 0
    high = len(arr) - 1
    mid = 0

    while low <= high:
        mid = int((high + low) / 2)
        if arr[mid] < x:
            low = mid + 1
        elif arr[mid] > x:
            high = mid - 1
        else:
            return mid
    return -1

arr = [2, 3, 4, 10, 40]
x = 10

result = binary_search(arr, x)

if result != -1:
    print(f"{x} ketemu di index {result}")
else:
    print(f"{x} tidak ketemu")

1.3 Jump Search

Algoritma selanjutnya mirip dengan kombinasi dari Binary Search dan Linear Search. Kemiripan tersebut karena jump search melakukan pencarian dengan melompati beberapa data sekaligus mirip dengan Binary Searcg dan melakuan pengecekan ke setiap data setelahnya mirip Linear Search. Untuk lebih jelasnya perhatikan langkah - langkah berikut:

1. Algoritma melakukan pengecekan terhadap indeks 0 dari data.
2. Jika data awal bukan data yang dicari maka pencarian akan langsung dilanjutkan dengan meloncati data sejumlah akar(n) dengan n merupakan panjang data.
3. Dilakukan pengecekan apakah data yang dicari lebih beasr atau lebih kecil dari data yang diakses saat ini.
4. Jika lebih besar maka pencarian akan dilanjutkan dengan meloncati sejumlah akar(n) data kembali. Namun, jika lebih kecil atau sama dengan maka pencarian akan dilakukan dengan linear search secara mundur hingga ditemukan data yang dicari.

Adapun berikut merupakan ilustrasi dari Jump Search:

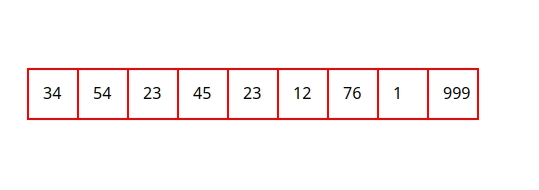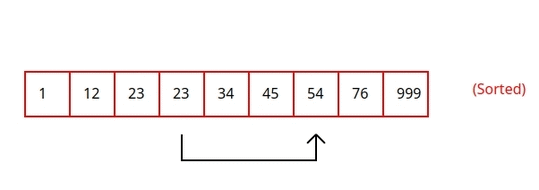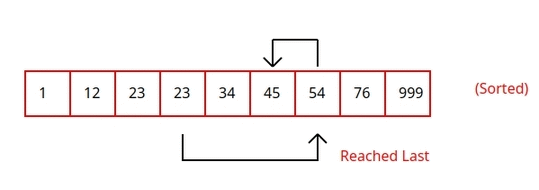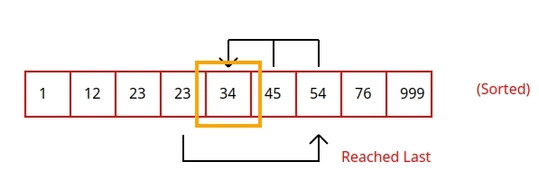
Berikut implementasi dari Jump Search pada Python:

import math

def JumpSearch(arr, x):
    start = 0
    end = int(math.sqrt(len(arr)))
    while (arr[end] < x and start < len(arr)):
        start = end
        end += end
        if (end > len(arr) - 1):
            end = len(arr) - 1
            break
    for i in range(end, start - 1, -1):
        if (arr[i] == x):
            return i
    return - 1

angka = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
x = int(input())
cari = JumpSearch(angka, x)
if (cari != -1):
    print(f'{x} ditemukan di indeks {cari}')
else:
    print("tidak ditemukan")

1.4 Interpolation Search

Algoritma selanjutnya merupakan pengembangan dari algoritma binary search. Bentuk pengembangan tersebut berada pada pemilihan nilai midnya, jika pada binary search mid akan selalu diambil dari nilai tengah panjang list tetapi pada interpoation search mid diambil dari perhitungan rentang nilai list atau besar persebaran dari nilai - nilai pada list. Sama seperti binary search dan jump search, algoritma ini memerlukan data - data yang telah terurut.

Adapun untuk mencari persebaran datanya digunakan perhitungan sebagai berikut:

mid = low + ((high - low)//(arr[high] - arr[low])) * (x-arr[low])

def interpolate_search(arr, x):
    low = 0
    high = len(arr) - 1
    mid = low + ((high - low)//(arr[high] - arr[low])) * (x-arr[low])

    while low <= high:
        mid = low + ((high - low)//(arr[high] - arr[low])) * (x-arr[low])
        if arr[mid] < x:
            low = mid + 1
        elif arr[mid] > x:
            high = mid - 1
        else:
            return mid

    return -1

arr = [2, 3, 4, 10, 40]
x = 10

result = interpolate_search(arr, x)

if result != -1:
    print(f"{x} ketemu di index {result}")
else:
    print(f"{x} tidak ketemu")