• 선형 구조보다 좀 더 빠른 속도를 기대할 수 있는 알고리즘
  • 선형 구조는 일반적으로 i번쨰 값을 탐색한 뒤의 i+1이 정해진 자료구조를 뜻한다. 반대로 선형구조가 아닌 자료구조를 비선형 구조라고 한다.
• 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있음
• 데이터가 무작위일 때는 사용할 수 없지만, 이미 정렬되어 있다면 매우 빠르게 데이터를 찾을 수 있다.
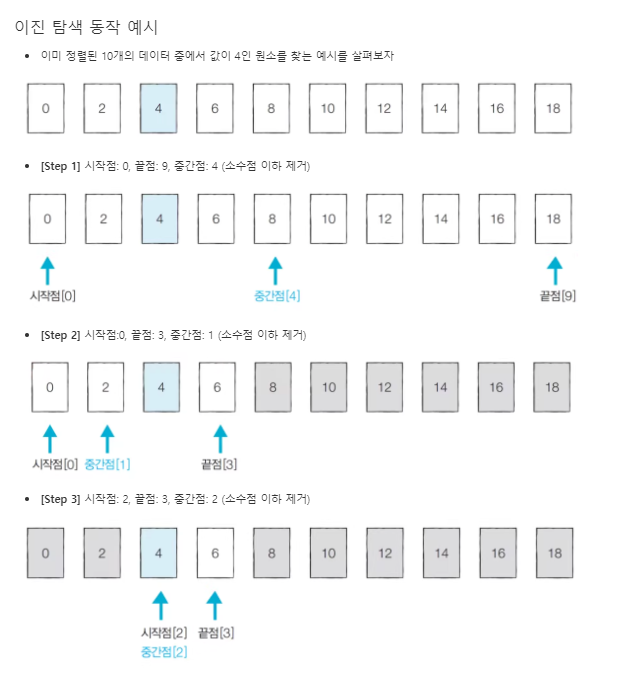
• 위치를 나타내는 변수 3개를 사용하는데 탐색하고자 하는 범위의 시작점, 끝점, 중간점을 말한다.
  • 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 알고리즘
• 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색함

배열 1 3 4 7 8 13 17에서 '8'이 있는 위치를 찾는다고 가정하자.

• 배열: 1 3 4 7 8 13 17
• 1st:총 배열의 가운데인 7을 선택.
• 7<8 이므로 더 큰 숫자가 있는 오른쪽으로 진행.
• 2nd:7~17의 배열중 가운데인 13을 선택.
• 13>8 이므로 더 작은 숫자가 있는 왼쪽으로 진행.
• 3rd:7과 13의 가운데에 있는 8을 선택.
• 8=8 이고 배열은 5번째이므로 답은 5이다.

• 단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는 log₂𝑁에 비례한다
• 예를 들어 초기 데이터 개수가 32개일 때, 이상적으로 1단계를 거치면 16개가량의 데이터만 남는다
  • 2단계를 거치면 8개가량의 데이터만 남는다
  • 3단계를 거치면 4개가량의 데이터만 남는다
• 다시 말해 이진 탐색은 탐색 범위를 절반씩 줄이며, 시간 복잡도는 **𝑂(log2 𝑁) **을 보장한다

#include <iostream>
#include <vector>
#include <string>

using namespace std;

int BinarySearch(vector<int> inputArray, const int arraySize, const int findData);

int main(void) {
	vector<int> v{ 1, 3, 4, 7, 8, 13, 17 };

	int result;
	result = BinarySearch(v, v.size(), 8);
	cout << result << endl;
	

	return 0;
}

int BinarySearch(vector<int> inputArray, const int arraySize, const int findData) {
	// argument (vector, vector Å©±â, ã´Â µ¥ÀÌÅÍ)
	int middleIndex;
	int startIndex = 0;
	int endIndex = arraySize - 1;
	
	while (endIndex - startIndex >= 0)
	{
		middleIndex = (startIndex + endIndex) / 2;
		if (inputArray[middleIndex] == findData) {
			return middleIndex + 1;
		}
		
		if (inputArray[middleIndex] < findData) {
			startIndex = middleIndex + 1;
		}
		else {
			endIndex = middleIndex - 1;
		}
	}
	return -1;
}

트리 자료구조 중에서 가장 간단한 형태가 이진 탐색 트리이다. 이진 탐새 트리는 다음과 같은 특징을 가진다.

• 부모 노드보다 왼쪽 자식 노드가 작다.
• 부모 노드보다 오른족 자식 노드가 크다.

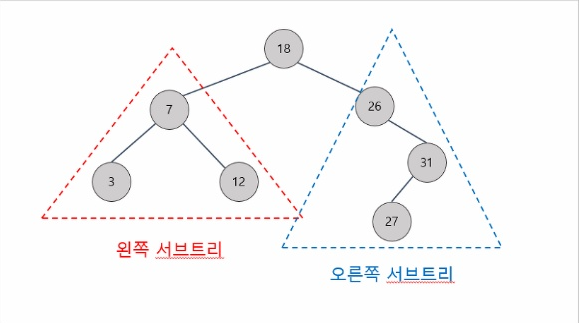
여기세 제일 위에 있는 부모 노드(18)이 이진 탐색 알고리즘의 중간값이라고 생각하면 된다. 왼쪽 서브트리로 가면 7이 중간값이 된다.

만약 12라는 데이터를 찾으려면 중간값인 18보다 작으므로 왼쪽으로 간다. 그리고 7보다는 크므로 오른쪽으로 가면 12가 존재한다.

이진 탐색 트리는 이진트리와 완전히 같게 배치되면 𝑂(log2 𝑁) 이지만, 최악의 경우 O(N) 의 시간 복잡도를 가진다.

• 시리즈:수학인듯 과학아닌 공학같은 컴퓨터과학/알고리즘 기초
• [이것이 코딩 테스트다 with Python] 26강 이진 탐색 개요
• <이진 탐색트리> 탐색, 삽입, 삭제 알고리즘 및 시간복잡도 분석