I numeri reali non possono essere rappresentati senza errore sui calcolatori. Infatti, questi vengono rappresentati (ad esempio sulle calcolatrici) con la notazione scientifica, ovvero normalizzando il numero.

Normalizzare un numero significa scriverlo nella forma: 2,34 x 10⁸. L'idea è quella di sbagliare di poco sui numeri piccoli, e poter sbagliare "di molto" sui numeri grandi; quindi dobbiamo trovare una rappresentazione che faccia un errore relativo tra il numero rappresentato ed il numero reale.

Inoltre, si tende ad avere un'unica cifra prima della parte decimale, questo perchè è proprio la rappresentazione che ci permette di rappresentare il numero più grande possibile con meno cifre possibile.

Ci permette di avere la massima precisione possibile, occupando il minor spazio possibile.

Questa notazione viene detta floating point perchè possiamo "spostare" la virgola a destra e a sinistra per rappresentare il numero.

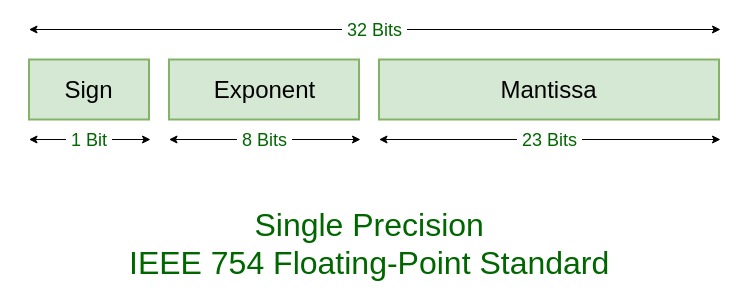
Viene usata per i numeri reali, quindi in C float (32 bit) e double (64 bit).

E' definito dallo standard IEEE.

Prima di questo standard c'era una divergenza delle rappresentazioni, infatti ogni sviluppatore sviluppava le proprie librerie con il "proprio" standard; quindi a seconda di dove il programma veniva compilato, si ottenevano risultati diversi.

Ai giorni nostri quasi tutti i sistemi utilizzano questo standard, ed abbiamo due rappresentazioni:

• singola precisione - 32 bit - float
• doppia precisione - 64 bit - double

L'idea è rappresentare un numero reale mediante una stringa di bit, è presente il segno (a differenza degli interi con il complemento a due);

Troviamo nella parte più significativa, i bit che rappresentano l'esponente, successivamente troviamo la parte frazionaria del numero.

A parole possiamo dire che 0 = - ed 1 = +, Usando la matematica invece: segno = (-1)^S.

Un numero normalizzato, ha sempre un 1 in testa: +-1.xxxx; se i numeri sono normalizzati, è inutile sprecare un bit per rappresentare quell'1, visto che è sempre uguale.

Quindi, per la rappresentazione normalizzata si fa finta di avere un 1, che in realtà non viene normalizzato.

Otteniamo quindi:

x = (-1)^S x (1+Fraction) x 2^{Esponente - bias}

L'esponente viene rappresentato con una strana rappresentazione, quindi nè segno in modulo ne rappresentazione a complemento a due.

Viene usata una rappresentazione chiamata rappresentazione per eccessi, in inglese Bias, che porta i numeri negativi tutta dalla parte dei positivi, sommando una costante in modo da renderli tutti positivi (aggiungo una costante di polarizzazione).

Quindi, se voglio avere il valore effettivo dell'esponente devo sottrarre questa costante di polarizzazione:

• Singola precisione : Bias = 127
• Doppia precisione : Bias = 1023

Inoltre, due configurazioni dell'esponente non vengono usate, perchè riservate: 00000000 e 11111111.

Il valore più piccolo è quando abbiamo un esponente del tipo: 00000001, e l'esponente vale quindi: esponente = 1- 127 = -126 (127 è la costante nel float). In deciamale questo valore corrisponde a : +-1.2 x 10^-38

L'esponente vale 11111110, quindi: esponente 254 - 127 = +127.

Otteniamo quindi: +- 3.4 x 10³⁸

Lo standard è lo stesso, ma cambiano i valori rappresentabili:

il valore più piccolo rappresentabile è con un esponente pari a 1 - 1023 = -1022 . Otteniamo quindi +- 2.2 x 10^-308

Abbiamo un esponente del tipo: 2046 - 1023 = +1023, ottenendo: +-1.8 x 10³⁰⁸

Anche se possiamo rappresentare questi numeri mostruosamente piccoli, ciò non significa che la precisione sia accettabile. Possiamo infatti rappresentare (realmente) questi range:

Approssimativamente 2^-23, quindi sei cifre decimali

Approssimativamente 2^-52, quindi 16 cifre decimali

🏁 esempi a 0:27 del 03-26

Si, sicuramente lo zero.

Supponiamo di avere un numero molto piccolo : 0.000---1. Come. posso normalizzarlo? Dovrei shiftarlo a sinistra tante volte finché non ottengo: 1.000--- .

Per ogni shift a sinistra, devo decrementare l'esponente. Se il numero è davvero molto piccolo, però, non ho abbastanza "esponenti" per poterlo normalizzare (portare 1 in prima posizione).

Quindi, un numero non normalizzabile è un numero talmente piccolo che gli esponenti a disposizione non bastano per normalizzarlo.

Lo zero, ad esempio, non ha letteralmente un numero da portare in prima posizione; viene utilizzato uno standard diverso per normalizzare lo zero e tutti i numeri molto vicini ad esso.

Il bit hidden non è presente, quindi vale zero, ed il numero viene rappresentato nel seguente modo:

x = (-1)^S x (0 + Frazione) x 2^-Bias

Il -Bias è un numero, che è più piccolo dell'esponente che potevamo usare nella precedente rappresentazione. Nel caso in cui la parte frazionaria sia composta da tutti zeri, il numero rappresentato è esattamente lo zero.

Questa rappresentazione ha un problema, ovvero ha due rappresentazioni per lo zero, per via del segno.

La configurazione di esponente 1111...1,, con parte frazionale == 0, viene fatto corrispondere ad infinito.

La configurazione di esponente 1111...1,, con parte frazionale =!= 0, viene fatto corrispondere NaN, ovvero Not A Number.

🏁 0:57

Questo tipo di standard non è facile da implementare. Piuttosto di scegliere delle soluzioni semplici da implementare in hardware, sono state scelte delle soluzioni che portavano una buona precisione nei risultati.

Questo è il motivo per cui i processori a basso costo non implementano tutte le operazioni floating point; infatti inizialmente il FP era gestito opportunamente solo da Intel, proprio perchè è stata intel ad implementare per prima la gestione del FP.

Vogliamo sommare 9.999 x 10¹ + 1.610 x 10 ^-1.

Non possiamo sommare direttamente i due numeri perchè le potenze utilizzate devono essere le stesse, quindi dobbiamo allineare i due numeri.

Per portare i due esponenti allo stesso livello abbiamo due scelte:

Se portiamo l'esponente più piccolo a quello più grande, dobbiamo spostare la virgola di due posizioni, ottenendo:

1.610 -> 0.016

In questa operazione andiamo inevitabilmente a perdere precisione, proprio perchè le cifre visualizzate sono sempre 4.

A questo punto non ci resta che moltiplicare le due cifre, ottenendo 10.015 x 10¹.

Questo numero, però, non è normalizzato; dobbiamo quindi shiftare ulteriormente le cifre per ottenere 1.0015 x 10² (dobbiamo poi approssimare).

Un addizionatore FP hardware è sicuramente un circuito più complesso di un adder ad interi; non è assolutamente pensare di poter eseguire tutta l'operazione in un unico giro di clock, questo perchè richiederebbe una quantità di tempo maggiore per ciclo di clock.

E' meglio quindi suddividere delle istruzioni più complesse in più colpi di clock, in modo da non penalizzare le altre operazioni.

Gli adder FP solitamente possono essere pipelined, ovvero mentre sta compiendo un'operazione, può iniziarne altre in modo da velocizzare il tutto.

A differenza dell'addizione, l'esponente non deve essere lo stesso per i vari operandi. Se volessimo moltiplicare:

1.110 x 10¹⁰ * 9.200 x 10^-5

Dobbiamo quindi sommare gli esponenti, e moltiplicare le parti significative, ottenendo: 10.2021 x 10⁵, dobbiamo infine normalizzare ed arrotondare, ottenendo: 1.021 x 10⁶.

A differenza dell'addizione, nella moltiplicazione abbiamo un ulteriore passaggio; dobbiamo infatti determinare il segno del risultato.

A volte potremmo dover portare un intero in float o viceversa; tipicamente queste operazioni richiedono, ovviamente, più cicli di clock, e possono inoltre essere pipelined.

Singola precisione:

• fadd.s

• fsub.s

• fmul.s

• fdiv.s

• fsqrt.s

  • Ad esempio: fadds.s f2, f4, f6

Doppia precisione:

• fadd.d

• fsub.d

• fmul.d

• fdiv.d

• fsqrt.d

  • Ad esempio: fadd.d f2, f4, f6

Programma in C

float f2c (float fahr){

    return ((5.0 / 9.0) * fahr - 32.0);

}

Codice assembly

f2c:
    flw f0, const5(gp)
    flw f1, const9(gp)
    fdiv.s f0, f0, f1
    flw f1, const32(gp)
    fsub.s f10, f10, f1
    fmul.s f10, f0, f10
    jalr   zero, 0(ra)

Con l'istruzione flw f0, const5(gp) stiamo caricando in memoria un valore floating point a singola precisione; l'istruzione sta per "Floating-point Load Word".

Dobbiamo ovviamente utilizzare dei registri appositi, ovvero i registri floating point; il primo registro usato è l'f0.

Questa soluzione è poco efficiente perchè stiamo salvando i valori 5 e 9 in dei registri e sopratutto stiamo effettuando una divisione fp ogni volta che dobbiamo effettuare una conversione;

sarebbe più intelligente avere sempre a disposizione questo valore, o meglio ancora calcolare le costanti a tempo di compilazione, in modo da evitare di aggiungere calcoli inutili a tempo di esecuzione.

Inoltre, i compilatori, quando si trovano a dover dividere per una COSTANTE, calcolano l'inverso del valore, ed invece di effettuare una divisione, effettuano una moltiplicazione; questo perchè le divisioni sono particolarmente lente.

fine lezione 10