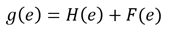The first algorithm that was chosen for this project was the A* Algorithm, either because calculating the heuristics of the problem or the various formulas that need to be applied were challenging.

If you don't know what this algorithm is about, you can take a look at some web pages like this one that explain what this search technique consists of. As previously mentioned, this algorithm requires a heuristic function and an evaluation function for each state of the game.

Heuristic of this problem

The heuristic of this function will be defined by the distance from Manhattan. This distance roughly measures the actual distance between two coordinates on the board. In general between two points (i1, j1) and (i2, j2), the distance is calculated as the sum of the absolute values ​​of the subtraction of each component i and j:

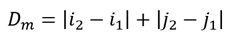
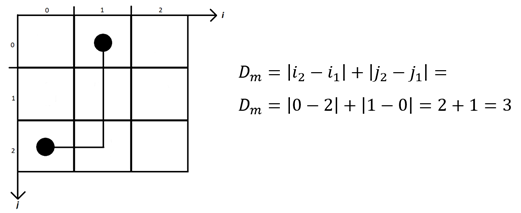
For example, for the distance between the points (2,0) and (0,1):

Therefore, knowing that, we will have that our heuristic will be based on the sum of all the distances of Manhattan between each cell out of its place with its final position:

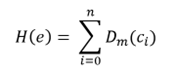
Note that H(e) is the heuristic of the state of board e and Dm is the distance from Manhattan to chip number i on the board. It is easy to see that it is not necessary to check that this sum never overestimates the real cost (of actions) until reaching the correct cell position, since such rectilinear displacements cannot be carried out in reality.

Evaluation Function

We also need an evaluation function for each node, to provide more information to each state and when evaluating nodes, we choose the best option. To do this, we will establish the following criteria: Any cell that is out of its final position on the board will be counted, thus obtaining a total of cells that are out of position.

After creating this function, we must add it to the heuristics, so that we obtain a state function g such that: