Sequential Circuits - eclubiitk/EClub-Handbook GitHub Wiki

• Introduction
• SR Latch
  • NOR Latch
  • NAND Latch
• Flip Flops
  • SR Flip Flop
  • JK Flip Flop
  • D Flip Flop
  • T Flip Flop
• Registers
  • Shift Register
• Counters
  • Binary Ripple/ Asynchronous Counters
  • Decade Counter
  • State Diagrams
  • Synchronous Counter
  • Modulo-m Counter

Sequential circuits are circuits in which the present output depend on the present input as well as the past output/outputs. Basically, there's a memory element which stores the output and provides that as a feedback or another set of input to its own circuit to generate a new output.The basic difference between the sequential and combinational circuits are these memory blocks.

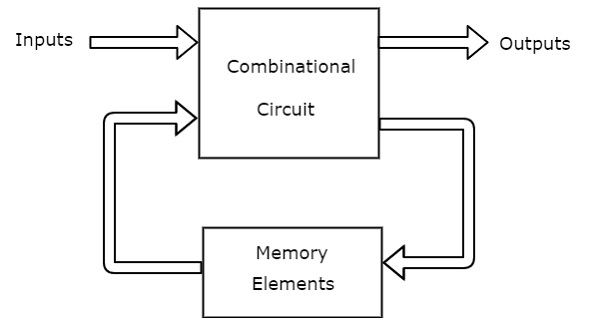
You can think of it as a counter which counts from 0 to 9 by adding 1 bit each time. So it adds 0+1=1, 1+1=2, 2+1=3...... and so it should know what the previous digit was or on what to add 1.Thus a memory element stores what the previous digit was.

These memory elements which are capable of storing one bit of information are known as flip flops.

Before coming to the flip flops, let's know about latches which are the most basic and primitive form of flip flops and used as memory elements. Certain types of latches are:

It is the Set Reset Latch and there are two forms of it using the NOR gate and the NAND gate.

1. NOR Latch

Two cross coupled NOR gates

R:Reset ,S:Set , Q and Q' : Complementary outputs

• Q = 1 and Q' = 0 : Set state of the Latch

• Q = 0 and Q' = 1 : Reset state of the Latch

  Recall for NOR gates: any input if 1 will make the output 0 , output will be 1 only if all inputs are 0

Now let's look at the different cases:

Now make S = 1 ( keeping R = 0 ) => Immediately Q' = 0 , and it is fed back to NOR1, which already has one of its input (R) = 0

=> Q = 1 (and Q' = 0 ) => Set state of the latch

Now if we remove the inputs it should retain the output as it is working as a memory element. Thus making S=0 & R=0 and Q' = 0 will lead to Q remaining as 1

When Q fed to second NOR it would let Q'=0 thus serving as memory storage.

Now make R = 1 ( keeping S = 0 ) immediately Q = 0 , and it is fed back to NOR2, which already has one of its i/p (S) = 0

=> Q' = 1 (and Q = 0 )

=>Reset state of the latch

Thus when now, R = 0 & S = 0, this would make no difference to the output. Hence memory action.

When S = 1 and R = 1 both Q = 0 and Q' = 0 irrespective of the previous inputs.

Thus now when S = 0 and R = 0 in memory state since both Q and Q' are 0, it would lead to making either Q or Q' equal to 1 whichever input reached faster the other NOR gate. Thus the purpose of storing the output is not served.

For NOR Latch, S= 1 & R = 1 condition is Not Allowed.

The truth table of NOR Latch is:

S	R	Q	State
0	0	Previous State	No Change
0	1	0	Reset
1	0	1	Set
1	1	?	Forbidden

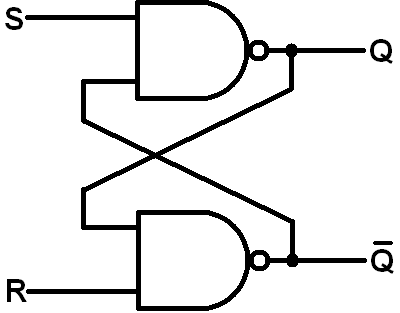
2. NAND Latch

Circuit Diagram:

• Two cross - coupled NAND gates.

• Note the difference with NOR.

Latch : Here, S drives the Q output and R drives the Q' output

=>Exactly opposite to that of NOR Latch

Recall : For NAND gates : Any (or both) input 0 will make the output 1 , for output to be 0, both inputs must be 1

Now, if S is made 0 ( with R at 1 ), Q becomes 1 , fed back to NAND2, and with R and Q both 1, Q' = 0 .The latch is now Set

If now S is reverted to 1 with R = 1 , no change in the outputs (memory action)

Now if S = 1 and R = 0 , Q' becomes 1 , fed back to NAND1, and with S and Q' both 1, Q =0 .The latch is now Reset.

If now R is reverted to 1 and S = 1 , there's no change in the outputs (memory action)

Now if we make S = 0 , R = 0 , both Q and Q' become 1. The same inconsistency as the NOR latch.

Hence this combination is not allowed

The truth table of NAND Latch is:

S	R	Q	State
1	1	Previous State	No change
1	0	0	Reset
0	1	1	Set
0	0	?	Forbidden

The basic difference between a latch and a flip flop is that laches are level triggered while flip flops are edge triggered. There is a clock pulse attached with the flip flop and the flip flop works on the rising and falling edge of the clock.

A clock is necessary because otherwise the inputs can change on their own and the storage of the previous output would not be made of much use.

Having understood the latches, flip flops are really easy to understand. Let's first go with the SR flip flop.

If the clock pulse is 0 above then the next part of the flip flop which is simply a NAND SR Latch corresponds to the memory state as both inputs would be 1 to the latch.

If the clock pulse is 1 then S correspnds to (S.clk(1))' = S' and R = R' and the truth table is:

Clk	S	R	Q	Q'
0	x	x	Memory	Memory
1	0	0	Memory	Memory
1	0	1	0	1
1	1	0	1	0
1	1	1	-	-

OR

Clk	S	R	Q(n+1)
0	x	x	Q(n)
1	0	0	Q(n)
1	0	1	0
1	1	0	1
1	1	1	-

Here if S = 0 and R = 0 it would provide the SR latch with 1 and 1 hence the memory state.Similarly for others. If we look at the last case it would provide the SR Latch with 0 and 0 hence the forbidden condition which is an anomaly of the SR flip flop and this leads to the JK Flip Flop.

The characteristic table is:

Q(n)	S	R	Q(n+1)
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	-
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	-

You don't need to memorize this , just by looking at the truth table you can make the characteristic table by looking at the values of S,R,Q(n) to find the value of Q(n+1) like for S = 0, R = 0, Q(n) = 0 => Q(n+1) = Q(n) = 0.

There is also one excitation table in which we have the outputs(Q(n) & Q(n+1)) with us and we need to compute the inputs (S,R) with it.

Q(n)	Q(n+1)	S	R
0	0	0	X
0	1	1	0
1	0	0	1
1	1	X	0

Due to the shortcoming of the SR flip flop, JK flip flop in which for every set of input there is an output. It is completely similar to the SR flip flop just having an output value for the forbidden states also.

J	K	Q	Q*
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

The truth table shown above have just the order of inputs different. You can easily understand it by referring below.

The outputs Q and Q' are fed back as inputs which make the difference. Now when clk=J=K=1 and let's say Q =0 and Q'=1. Now when Q is fed to the NAND2 it would result 1, and when Q' is fed to NAND1 it would result 0. Thus comparing with the part2 which is the NAND latch it would result Q=1 and Q'=0.

Now when it is again given as feedback, this would result 1 from NAND1 and 0 from NAND2 thus changing the outputs Q=0 and Q'=1. So it feels as if it results in Q(n)' on every run.

Clk	S	R	Q(n+1)
0	x	x	Q(n)
1	0	0	Q(n)
1	0	1	0
1	1	0	1
1	1	1	Q(n)'

If J=K=1, and if clk=1 for a long period of time, then Q output will toggle as long as CLK is high, which makes the output of the flip-flop unstable or uncertain. This problem is called race around condition in J-K flip-flop.

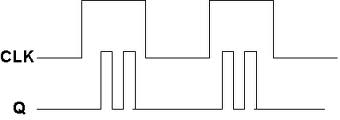
This problem (Race Around Condition) can be avoided by ensuring that the clock input is at logic “1” only for a very short time. This introduced the concept of Master Slave JK flip flop.

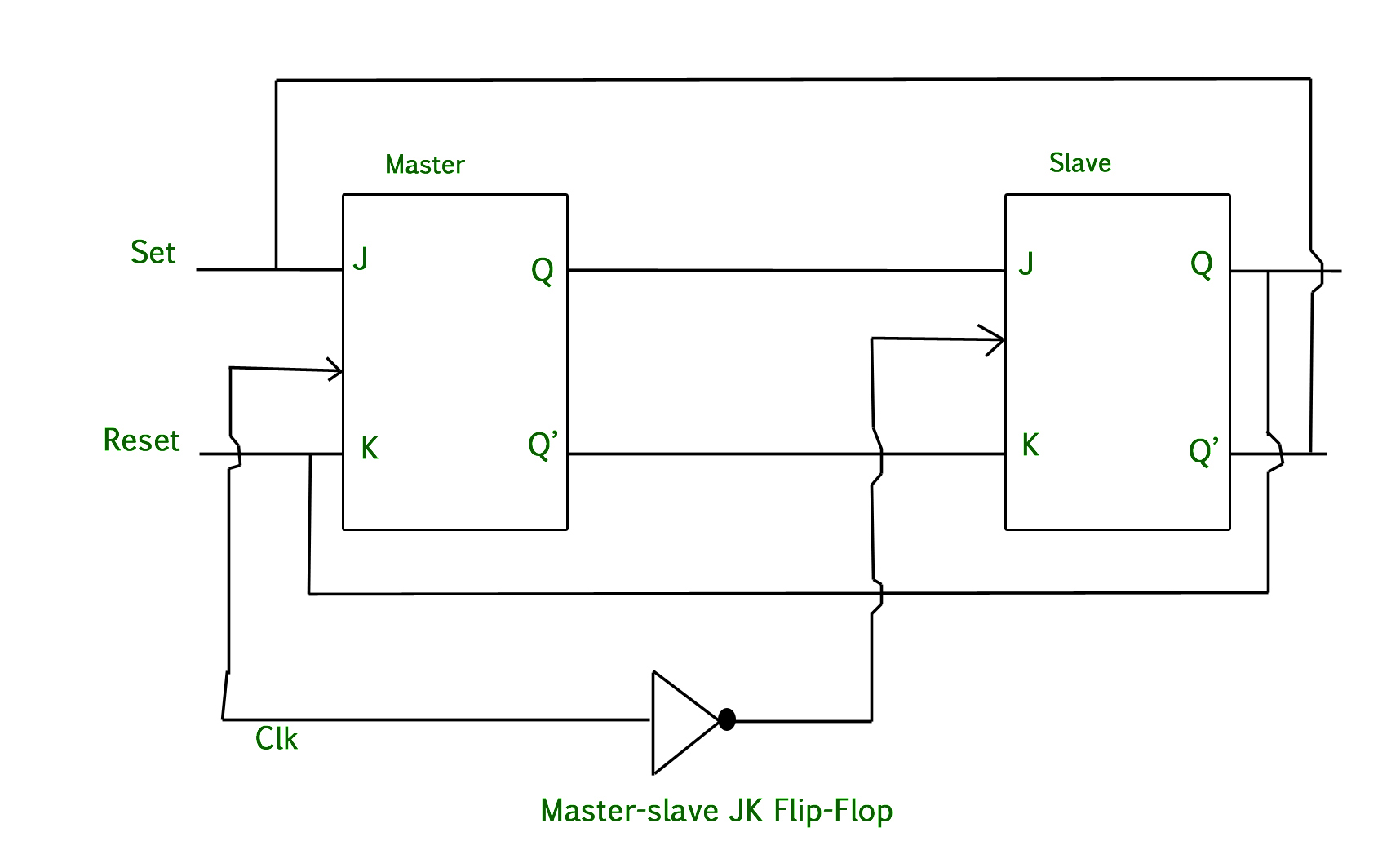
The two blocks refer to the actual structure of the J K filp flop. In the master-slave condition another JK flip flop is added and the ouput of the second flip flop is feedbacked as input to the first flip flop + the same clock is attached with a NOT gate.

The problem of race around arises when CLK=J=K=1 , so let's discuss that case.First see this:

When the clock starts , master FF functions and the slave FF acts as a memory state as the clock signal is zero due to NOT gate. Now when J=1 and K=1 and on the rising edge of the clock , the Q signal becomes high of master FF and it would remain high till the second rising edge.

On the falling edge of the clock the slave FF becomes active and the master FF acts as a memory state, thus it would remain high as said above.Now output of first FF is fed to slave FF which produces the same output as master FF thus it remains high till the second falling edge.

That output is fed back to master FF and on the second rising edge(means slave FF acts as memory state now), toggling takes place and thus the sginal Q(m) becomes low. Now, at the second falling edge, again the input is given to slave FF and toggling takes place and the process repeats itself.

This makes the Master-Slave J-K flip flop a Synchronous device as it only passes data with the timing of the clock signal

Q	D	Q*
0	0	0
0	1	1
1	0	0
1	1	1

T	Q	Q*
0	0	0
0	1	1
1	0	1
1	1	0

Till now we know that Flip Flops are a part of sequential circuits and can be used to store a single bit of binary data (1 or 0). However, in order to store multiple bits of data, we need multiple flip flops.

A Register is a device which is used to store such information. It is a group of flip flops connected in series and used to store multiple bits of data. The N-bit register consists of N number of Flip Flops and thus stores a N-bit number.

There are two types of registers: parallel and serial registers. They differ in the manner in which the binary data is loaded and retrieved from them.

• For serial form, one bit is input at a time(SI) and so we even receive a serial output(SO).
• For parallel form, data is entered individually to all the F/Fs(PI) and received as parallel outputs(PO).

For a 4-bit register, we thus use 4 Flip-Flops. Since we just want data to be stored without toggling, we will use a D Flip-Flop. A clock is internally connected to all the four F/Fs to govern the operation. So, we are bound to follow the clock.

Whatever input we give to the F/Fs gets changed after one time period of the clock. Here, for negative trigerred flip flops, value changes on reaching from one falling edge to another. Thus, for the next clock pulse, we will have different combination of bits stored.

• Thereby, we use an independently controlled Load.

When we want register inputs to remain unchanged (even with clock changes), we can use a load control input. The load input determines whether the next pulse will accept new information or leave the information in the register intact.

The Load input, when set at logic level 1 (high state), sets the four flip-flop data inputs to the register's four input bits. That is, we load the data into the register. When Load is at logic level 0 (low state), the four flip-flops have their outputs fed into their inputs. That is, the value stored doesn't change.

• There is also an additional direct reset input named CLEAR or RESET. When CLEAR is 0 the flip flop is resetting,independent of clock and D values. It is useful because in digital systems when the power is turned on the state of flip-flops is unknown. Direct input CLEAR can bring all flip-flops to the known starting state prior to the clock operation.

There are two types of Registers based on application, namely:

• Shift Register
• Storage Register

For simplicity, we will elaborate only Shift Registers.

A Shift register shifts its binary information in one or other direction. For example: by connecting the output of each D flip-flop to the input of another D flip flop in its right, each clock pulse shifts the content of the register, one bit position to the right.

The shift register, which allows serial input (one bit after the other through a single data line) and produces a serial output is known as Serial-In Serial-Out (SISO).

For a Right shift register, the serial input determines what goes into the leftmost flip flop during the shift. The serial output is taken from the output of the rightmost flip flop.

The logic circuit given below shows a serial-in serial-out shift register. The circuit consists of four D flip-flops which are connected in a serial manner. All these flip-flops are synchronous with each other since the same clock signal is applied to each flip flop.

So, it look like this:

How does a shift register work? The working is simple.

• Lets assume that all the flip-flops (1 to 4) have just been RESET (CLEAR input) and that all the outputs Q₀ to Q₃ are at logic level 0. The input we want to store is 1111.
• If a logic 1 is connected to the serial input pin of first flip flop, then on the first clock pulse the output of first D flip flop, and therefore the resulting Q₃ will be set HIGH to logic 1, with all the other outputs still remaining LOW at logic 0.
• Now, we give the next input 1. With D2 connected to Q3, D2 becomes 1 and so does Q2. So, now the resulting ouputs become 1100.
• In the similar way Q1 also becomes 1 and so does Q0 in the last step.
• Hence our stored data becomes 1111.

So, we draw the Table for the given data:

Clock Pulse	Q3	Q2	Q1	Q0
Initial	0	0	0	0
First	1	0	0	0
Second	1	1	0	0
Third	1	1	1	0
Fourth	1	1	1	1

Timing Diagram

Counter is apparently the widest application of flip-flops. As the name suggests, they are used in digital electronics for counting purpose, that is, they can count specific event happening in the circuit, often in relationship to a clock signal. In layman terms, counter counts the pulses.

UP counters count upwards or incrementally. It increases count for every rising/falling edge of clock depending upon positive/negative edge triggering of the flip flops.

Down counters on the other hand, count downwards or in a decremental manner.

Now an interesting point to be noted is that not only counting, a counter can follow a certain sequence based on our design, like any random sequence 0,1,3,2... !

Moving to the circuit design, counters are groups of flip-flops and as we know, flip-flops have a clock input, so depending on the type of clock input, counters are classified as:

• Asynchronous or ripple counters
• Synchronous counters

Before moving forward, there are two major points to be considered:

• A counter following binary number sequence is called Binary Counter. We'll be using this term hereby.
• An n bit binary counter consists of n flip-flops and can count in binary from 0 to (2ⁿ – 1).

In an asynchronous counter we don’t use universal clock, only first flip flop is driven by main clock and the output of the first flip flop is the clock input of the second flip flop and so on. Since it is an UP Counter, it counts from a lower to higher value.

They are of following types:

• N-bit asynchronous UP counter
• N-bit asynchronous DOWN counter
• N-bit asynchronous UP/DOWN counter

For simplicity and understanding, we will study 4-bit asynchronous UP counter in detail:

For a 4-Bit Binary Asynchronous Counter, we use 4 JK flip flops(can also use T flip flops as when J=K=1), and it can count from 0 to (2⁴-1), 0 to 15.

The output Q₀ of the first F/F is given as input clock to second F/F and output Q₁ of second is acting as clock for third F/F and so on.

However, for a slight change, it uses 4 bits to count decimal numbers from 0 to 9 (0000 to 1001) and then goes back to 0. The rest of the numbers (10 to 15 (1010 to 1111) are DON'T CARE (X) in K map, and do not appear in Counters.

A 4-bit asynchronous counter thus represents 10 states.

How does it work ?

Since this is a 4-bit counter, we need to consider 16 stated of the clock. The flip flops are negative edge triggered, so we consider falling edges for the change in the timing diagram.

Starting from output of the first F/F (Q₀), initially it is 0 and it remains 0 till the first falling edge, then it is complemented due to toggling and remains high till the next falling edge, then again low and so on.

For output of the second F/F (Q₀), Q₀ acts as a clock, and so we chnage state from low to high noticing the falling edge of Q₀.

Following the process, we similarly draw diagrams for Q₂and Q₃.

<

For the truth-table, Q₀ is the LSB and Q₃ is the MSB. Thus, we notice the states of all four outputs for 16 states and plot the table:

Clock Pulse	Q3	Q2	Q1	Q0
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1
10	1	0	1	0
11	1	0	1	1
12	1	1	0	0
13	1	1	0	1
14	1	1	1	0
15	1	1	1	1

As a simple modification of the UP counter. 4 bit DOWN counter will count numbers from 15 to 0, downwards. The output of the first flip flop will change, when the negative falling edge of clock signal occurs. Here every clock pulse at the input will reduce the count of the individual flip flop. So the down counter counts from 15, 14, 13...0 i.e.(1111 to 0000).

The block diagram of 4-bit Asynchronous binary down counter is similar to the block diagram of 4-bit Asynchronous binary up counter. But, the only difference is that instead of connecting the normal outputs of one stage flip-flop as clock signal for next stage flip-flop, connect the complemented outputs of one stage flip-flop as clock signal for next stage flip-flop.

A Decade Counter is a serial digital counter which goes through 10 unique combinations of outputs and then resets as the clock proceeds. It uses 4 bits to count in binary coded decimal numbers from 0 to 9 (0000 to 1001) and then goes back to 0. The rest of the numbers from 10 to 15 (1010 to 1111) are DON'T CARE (X) in K map, and do not appear in BCD Counters.

The circuit is essentially, a ripple counter which counts up to 16. We desire however, a circuit operation in which the count advance from 0 to 9 and then reset to 0 for a new cycle. This reset is a accomplished at the desired count as follows:

• With counter REST count = 0000 the counter is ready to stage counter cycle.
• The counter then starts counting from 0 till it reaches 1001(decimal 9).
• The next count pulse advance the count to 10 count = 1010. Now, we have to reset our flip flops!
• For this, we use 2 asynchronous inputs: Preset (PR) and Clear (CLR). As we know, when CLR=0; Output=0(RESET) and when PST=0; Output=1(SET). But here we need RESET action, hence Preset is connected to Logic 1, so it has no effect on flip flops.
• To make CLR=0, a logic NAND gate decodes the count of 10 providing a level change at that time which then resets all counter stages.

Thus, the pulse after the counter is at count = 9, effectively results in the counter going to count = 0.

Truth Table of a BCD ripple Counter is:

Clock Pulse	Q3	Q2	Q1	Q0
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1
10	0	0	0	0

A 3-bit flip flop starts from 000(decimal 0) to its maximum count (2³-1) which is equal to 111(decimal 7).

The states are namely the counts of our counter and depicting them pictorially is a State diagram. We know that a counter changes states with every passing clock pulse, this change is indicated by arrows.

Following is the state diagram of a simple 3-bit Up counter:

Similarly, following is the state diagram of a BCD up Counter:

If the clock pulses are applied to all the flip-flops in a counter simultaneously, then such a counter is called as synchronous counter. The one advantage of synchronous counter over asynchronous counter is that it can operate on a higher frequency than asynchronous counter as it does not have delay because of same clock given to each flip flop.

• Decide the number of Flip Flops.
• Draw the Excitation Table of the flip flop.
• Draw the state diagram of the counter and circuit excitation table.
• Obtain simplified equation using K-Map.
• Draw the logic diagram.

Here, lets complete these steps and design a 3-bit synchronous counter using JK flip flop.

We very well know how to make an excitation table for a JK flip flop.

Q	Q*	J	K
0	0	0	X
0	1	1	X
1	0	X	1
1	1	X	0

We've already seen the state dagram for 3-bit counter, so that step can be skipped.

For 3-bit, there are 8 states(0 to 7). The present states will be indicated by Q₂, Q₁. Q₀ while the next state will be shown as Q₂, Q₁, Q₀*.

It is very simple to write the next state of a counter using state diagram. The present state starts at 000 and the next state ends at 000.

To find the inputs of JK flip flop, we refer to the excitation table, notice the present and the next state and thus the generated input.

So, our circuit excitation table looks like this:

Q2	Q1	Q0	Q2*	Q1*	Q0*	J2	K2	J1	K1	J0	K0
0	0	0	0	0	1	0	X	0	X	1	X
0	0	1	0	1	0	0	X	1	X	X	1
0	1	0	0	1	1	0	X	X	0	1	X
0	1	1	1	0	0	1	X	X	1	X	1
1	0	0	1	0	1	X	0	0	X	1	X
1	0	1	1	1	0	X	0	1	X	X	1
1	1	0	1	1	1	X	0	X	0	1	X
1	1	1	0	0	0	X	1	X	1	X	1

Now, we need to make K map for the same. For total 6 JK inputs, we need to make 6 eight cells K maps, one for each input. We know that the DON'T CARE value(X) can be grouped with 1, so making possible groups and writing the expressions that follow, we obtain:

Having made the Kmap, we can easily design the logic diagram now.

• J₀ and K₀ are 1, so we connect them to logic value 1.
• J₁ and K₁ are equal to Q₀, so output of first flip flop is input to second.
• J₂ and K₂ are aquired through the AND of Q₀ and Q₁.

Thus, our logic diagram is ready !

• 2-bit up/down ripple counter is MOD-4 or modulus 4 counter.
• 3-bit up/down ripple counter is MOD-8 or modulus 8 counter. MOD number is equal to the number of bits,(2_n).

Now, an important point to be discussed here is, making a counter count to a particular value. A Modulo-m counter can also be made a Modulo-p counter, with p < m. Example: A Modulo-8 counter can be made to count only from 0 to 5, and thus, it becomesa Modulo-6 counter.

This is done using PRESET and CLR input, and with the use of NAND gate. We've already discussed something similar in a decade counter.