ML: Linear Regression - dudycooly/1235 GitHub Wiki
Introduction
Linear Regression is a statistical analysis for predicting the value of a quantitative variable. Based on a set of independent variables, we try to estimate the magnitude of a dependent variable which is the outcome variable.
In general, ML analyse the relation between a response/dependent variable (variable to be predicted) say y and predictor/independent (variable that affects the value of response variable) x and creates a model with a mapping function between them
y = f(x)
This Linear Regression algorithm works on philosophy the mapping between two variables x and y can be modelled by a straight line
The equation of such a line is
Using this equation, we should be able to predict value of y for any given value of x within in the range. We just need values for those coefficients
BestFit
If you notice not all data points are falling on regression line

The vertical lines between the data points and regression line are illustrating the deviation of predicated value from the actual value. This is called residual which makes up most of random error in the equation
Let us assume Best Fit fits all the points without any residual, then equation above can be treated as normal linear equation
y = mx +b
where
βo is intercept "b"
β1 is slope "m"
However Error is an inevitable part of the prediction-making process. No matter how powerful the algorithm we choose, there will always remain an (∈) irreducible error
We can't completely eliminate the (∈) error term, but we can still try to reduce it to the lowest. Such a regression line with lowest residual is called Best Fit line and the process is called fitting
Fitting Methods
There are different fitting methods
- Ordinary Least Square (OLS)
- Generalized Least Square
- Percentage Least Square
- Total Least Squares
- Least absolute deviation
- and many more.
Let us use the most preferred technique for regression i.e Ordinary Least Square (OLS) Conceptually, OLS technique tries to reduce the sum of squared errors ∑[Actual(y) - Predicted(y')]² by finding the best possible value of regression coefficients (β0 or b, β1 or m).
OLS formula for m and b are given as
(as explained on this Khan Academy video)
The slope formula can also be rewritten as follows (as explained on this video)
The slope can also be worked out as follows if correlation coefficient (R) and Standard Deviation of X and Y are known for the data
and by using this
The best fit line obtained using those values is also called as OLS regression line
Measuring Accuracy
How accurate is our model? How good is our best fit line ?
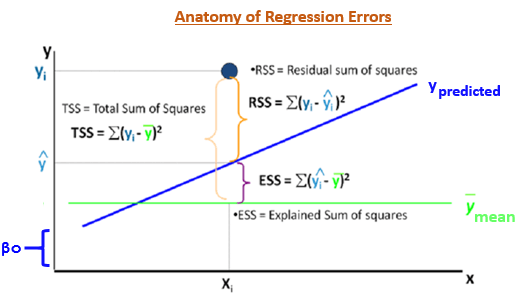
In OLS, the error estimates can be divided into three parts:
- Residual Sum of Squares (RSS) or Sum of Squared Errors (SSE) - ∑[Actual(y) - Predicted(y)]²
- Explained Sum of Squares (ESS) - ∑[Predicted(y) - Mean(ymean)]²
- Total Sum of Squares (TSS) - ∑[Actual(y) - Mean(ymean)]²
Following are some metrics you can use to evaluate your regression model. However these metrics can have different values based on the type of data. Hence, we need to be extremely careful while interpreting regression analysis.
- R Square (Coefficient of Determination) - tells us the amount of variance explained by the independent variables in the model (Great explanation by Khan Academy). Using these error terms defined above we can calculate Coefficient of Determination (R²) as follows
R² = 1 - (SSE/TSS)R² metric It ranges between 0 and 1. Usually, higher values are desirable but it rests on the data quality and domain. For example, if the data is noisy, you'd be happy to accept a model at low R² values. But it's a good practice to consider adjusted R² than R² to determine model fit. - Adjusted R²- The problem with R² is that it keeps on increasing as you increase the number of variables, regardless of the fact that the new variable is actually adding new information to the model. To overcome that, we use adjusted R² which doesn't increase (stays same or decrease) unless the newly added variable is truly useful.
- F Statistics - It evaluates the overall significance of the model. It is the ratio of explained variance by the model by unexplained variance. It compares the full model with an intercept only (no predictors) model. Its value can range between zero and any arbitrary large number. Naturally, higher the F statistics, better the model.
- RMSE / MSE / MAE - Error metric is the crucial evaluation number we must check. Since all these are errors, lower the number, better the model. Let's look at them one by one:
- MSE - This is mean squared error. It tends to amplify the impact of outliers on the model's accuracy. For example, suppose the actual y is 10 and predictive y is 30, the resultant MSE would be (30-10)² = 400.
- MAE - This is mean absolute error. It is robust against the effect of outliers. Using the previous example, the resultant MAE would be (30-10) = 20
- RMSE - This is root mean square error. It is interpreted as how far on an average, the residuals are from zero. It nullifies squared effect of MSE by square root and provides the result in original units as data. Here, the resultant RMSE would be √(30-10)² = 20. Don't get baffled when you see the same value of MAE and RMSE. Usually, we calculate these numbers after summing overall values (actual - predicted) from the data.
Is LR right choice?
Linear Regression may not fit for distribution for data without any relation

So before settling down on Linear Regression, ensure dataset satisfies following conditions 0. Linearity
- Nearly Normal Distribution of Residual Values
- Extrapolation (Insufficient Data)
- Homoscedasticity (Variability is constant for the entire range or distribution of residuals has to be described by the classic bell curve of the same width and heigh everywhere along the X axes).
https://gallery.shinyapps.io/slr_diag/