4th term 3nd week - dsuz/csharp GitHub Wiki

今回のテーマ

CSharp4-3.unitypackage をダウンロードして Unity のプロジェクトにインポートする。Assets/4-3 Dot Product/ 以下に今回の内容がある。

内積（ドット積・スカラー積、inner product, dot product, scalar product）の定義については教科書等（数学B）を参照せよ。

２つのベクトル・それらの内積・それらのなす角については以下の式が成り立つ。

$\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos\theta$

そして、以下の関係が成り立つ。

$\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos\theta$

$\Leftrightarrow \cos\theta=\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$

$\Leftrightarrow \theta=\arccos\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$

つまり、内積が計算できれば、なす角を求めることができる。

/4-3 Dot Product/1 Calc Angle/DotProduct シーンを実行し動作を確認せよ。このシーンでは線分 OP と OQ をそれぞれベクトルとして扱い、なす角を求めている。

このサンプルでは以下の２通りの方法で角度を求めている。

後者は前者を使っている。Visual Studio から Vector2.Angle() の定義を参照すると、メソッドの実装を見る事ができる。同様に Vector2.Dot() の定義を参照すると、内積の定義を見る事ができる。

ポイントは「内積を使うことで角度が求められる」ことであるが、Unity においてはそれを知らなくても２つのベクトルがなす角は Vector2.Angle() で求められるようになっている。また、求められた角度は180度を超えない。

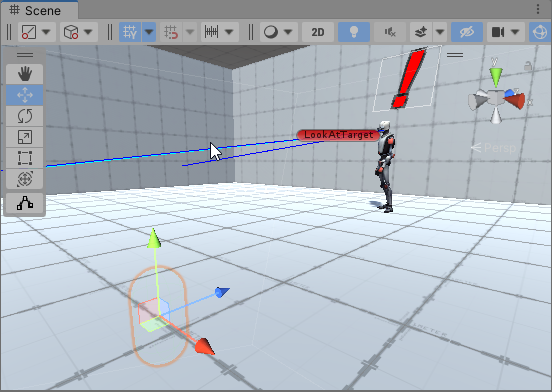
/4-3 Dot Product/2 Search Cone/Search Cone シーンを実行し動作を確認せよ。このシーンでは WASD でカプセルを操作することができる。各ロボットの視界に入るとロボットの頭上に！が表示される。ロボットの視界はシーンにギズモとして表示されている。

以下の方法で、カプセルがロボットの視界に入っているか判定している。

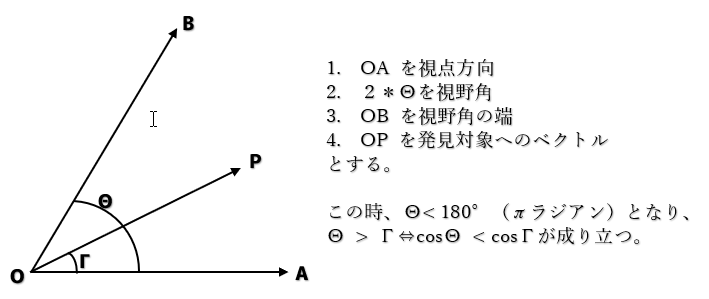
cosΘは普通に求められる。また、

$\overrightarrow{OA}\cdot\overrightarrow{OP}=|\overrightarrow{OA}||\overrightarrow{OP}|\cos\gamma$

により cosΓ も求められるので、視界に入っているか判定できる。

この処理は SightController コンポーネントで行われており、このコンポーネントはロボットの頭にアタッチされている。Hierarchy の検索機能を使って探すとよいでしょう。

判定は距離と角度のみで行っているため、高低差がある場合は以下のように地面に潜っているような場合にも視界に入っていると判定されてしまう。

高さの概念や壁がある場合は、これに加えて Ray などを使って追加の判定処理を行うなど工夫しなければならない。

視野を使った索敵は、コライダーで手軽に作ることもできる。

/4-3 Dot Product/3 Search Cone using Collider/Search Cone using Collider シーンでは ProBuilder を使って作ったメッシュと Mesh Collider を使って視界判定をしている。

固定のメッシュを使った場合、視野角など視界を再設定する時に再度モデリングしなければならない。視野角と距離のみを設定して調整するより手間がかかる。