4th term 2nd week - dsuz/csharp GitHub Wiki
今回のテーマ
- 外積 (Cross Product) と法線ベクトル (Normal Vector)
- 線分の交差判定
準備
CSharp4-2.unitypackage をダウンロードして Unity のプロジェクトにインポートする。Assets/4-2 Cross Product/ 以下に今回の内容がある。
外積とは
外積は数学用語であり、高校数学の範囲外だが問題を解くのに役立つため教える高校も多い。定義については調べれば見つかるが、今回重要なのは「2つのベクトルから求められる外積ベクトルはその2つのベクトルの両方と直交する」ということである。
ということは外積ベクトルは2つのベクトルで作られる平面に直交しているということである。平面に直交するベクトルの事を法線ベクトルという。
法線 (Normal) は頻出の言葉・概念であるため覚えておくこと。
また、外積ベクトルの求め方は Unity を使っている場合はとりあえず覚えなくてよい。Unity には外積ベクトルを計算するメソッドが用意されているためである。C# の標準ライブラリにも用意されている。
外積を見てみる
/1 What Is Cross Product/Cross Product シーンを実行し、Hierarchy 上のオブジェクト "A" と "B" の座標を動かしてみましょう。この時に表示される黄色いベクトルが外積です。
法線ベクトルを使う
/2 Use NORMAL/Keep it up シーンを実行し、画面をドラッグして線を引くとその上をカプセルが移動します。この時、カプセルは接線と垂直つまり法線ベクトルの方向に直立して移動します。
なお、Unity でコライダー(トリガーではない)を使って衝突を判定した時には以下の API により法線ベクトルを取得できます。
- 3D の場合 - ContactPoint.normal
- 2D の場合 - ContactPoint2D.normal
線分の交差を判定し、交点の座標を求める
/3 Simple Intersection (Crossing Lines)/Crossing Lines シーンを実行し、画面の説明に従って点 A, B, P, Q をドラッグすると、線分 AB と PQ の交差判定をして交差している時は交点座標を計算し、黒い点が交点に表示される。
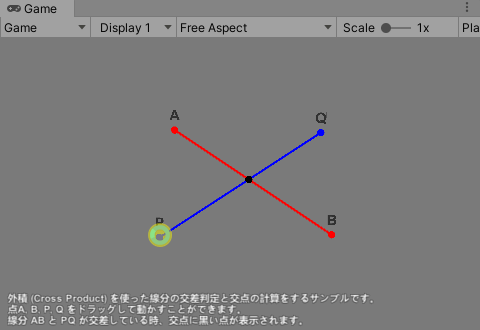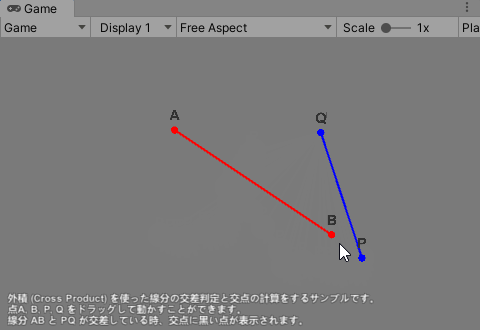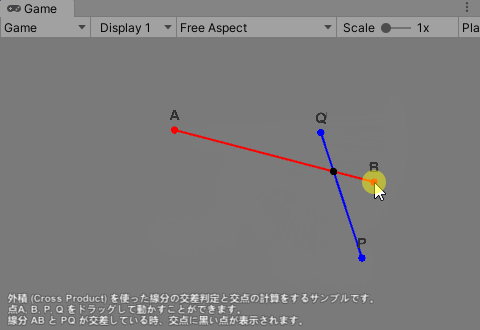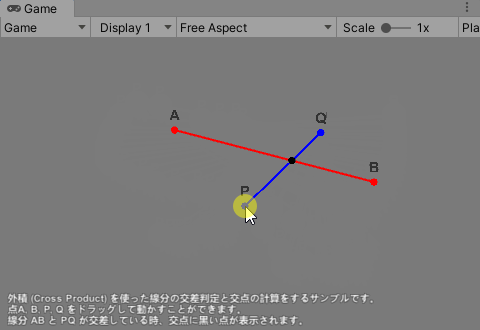
このサンプルにより「外積を使って線分の交差を判定し、交点の座標を求める)方法を学ぶ。
交差判定
交差判定の判定式は
Vector3.Cross(pq, pb).z * Vector3.Cross(pq, pa).z < 0 && Vector3.Cross(ab, ap).z * Vector3.Cross(ab, aq).z < 0
である。
Vector3.Cross(pq, pb).z * Vector3.Cross(pq, pa).z < 0 は、 $\vec {PQ}\times\vec {PB}$ と $\vec {PQ}\times\vec {PA}$ の向きが逆であることを意味する。
つまり、 $θ$ と $φ$ が逆方向である ⇔ $\vec {PQ}$ が $A$ と $B$ の間を通っていることを意味する。
Vector3.Cross(ab, ap).z * Vector3.Cross(ab, aq).z は、 $\vec {AP}\times\vec {AP}$ と $\vec {AB}\times\vec {AQ}$ の向きが逆であることを意味する。
つまり、 $θ'$ と $φ'$ が逆方向である ⇔ $\vec {AB}$ が $P$ と $Q$ の間を通っていることを意味する。
$\vec {PQ}$ が $A$ と $B$ の間を通っている、かつ、 $\vec {AB}$ が $P$ と $Q$ の間を通っている場合、線分 $PQ$ と線分 $AB$ は交差していることになる。
もし、
Vector3.Cross(pq, pb).z * Vector3.Cross(pq, pa).z < 0 が成り立っていないとすると、 $\vec {PQ}\times\vec {PB}$ と $\vec {PQ}\times\vec {PA}$ の向きが同じであり、 $θ$ と $φ$ が同じ方向であり、 $\vec {PQ}$ が $A$ と $B$ の間を通っていないことになり、線分 $PQ$ と線分 $AB$ は交差していないことになる。
参考
交点の求め方
交点座標は、 $A$ + $\vec{AB}$ * $\lvert\vec{AX}\rvert$ / ($\lvert\vec{AX}\rvert$ + $\lvert\vec{XB}\rvert$) である。ここでは $\lvert\vec{AX}\rvert$ と $\lvert\vec{XB}\rvert$ の比を求める必要がある。
ここで「 $\lvert\vec{AP}\times\vec{AQ}\rvert$ は $\vec{AP}$と $\vec{AQ}$ から成る平行四辺形の面積に等しい」という法則が使える。従って、 $\lvert\vec{AX}\rvert$ $:$ $\lvert\vec{XB}\rvert$ $=$ 三角形 $PQB$ の面積 $:$ 三角形 $PQA$ の面積 $=$ 平行四辺形 $PBQB'$ の面積 $:$ 平行四辺形 $PAQA'$ の面積 $=$ $\lvert\vec{BP}\times\vec{BQ}\rvert : \lvert\vec{AP}\times\vec{AQ}\rvert$ が成り立ち、交点座標が求められる。
応用(線が閉じていることを判定する)
/4 Enclosure/Enclosure シーンを実行し、画面をドラッグして線で囲むと、その中のオブジェクトが消えます。これはプログラムとしては以下のことをしています。
- ドラッグした座標に曲線を描く
- 曲線を線分の集まりとして、線分が交差していることを判定する(ここで外積を使う)
- 線分が交差していたら、曲線が閉じていると判定し、閉じた曲線を構成する座標から Polygon Collider 2D を構成する
- Polygon Collider 2D と接触しているコライダーをすべて破棄する
参考
過去問1 が外積を使った衝突判定の問題です