[attention] NLP with attention - dsindex/blog GitHub Wiki

Attention

mathematical definition

  • attention은 q, x(i), vector x(길이가 n)를 가지고 정의된다. 즉, q가 vector x의 요소인 x(i) 각각에 어느정도 attention을 둬야하는지 수치로 계산하는 방법이라고 할 수 있다. 따라서, 관련도를 계산하는 score f(x(i), q)를 어떻게 정의하는 지가 중요하다.

  • score / alignment function

    • additive attention(MLP attention)
      • sigmoid(W1 * x(i) + W2 * q) = d-dimension
        • sigmoid 대신 tanh를 사용하는 경우도 많다.
        • W1, W2는 d x d matrix로 가정. x(i), q는 column vector이고 '*'는 matrix multiplication.
      • 여기에 d-dimension w를 transpose해서 곱하면 scalar value 하나가 나온다.
      • 수식이 MLP 형태라서 MLP attention이라고 부르기도 한다.
    • multiplicative attention(dot-product attention)
      • W1 * x(i), W2 * q
        • W1, W2는 d x d matrix로 가정. x(i), q는 column vector이고 '*'는 matrix multiplication.
      • 이 두개의 d-dimension을 dot-product하면 scalar value 하나가 얻어진다.
      • dot-product attention이라고도 한다.
      • additive attention의 성능이 일반적으로 좀 더 좋다고 알려져 있지만, 메모리 사용량과 GPU에서 계산 최적화 등을 고려하면 multiplicative attention이 좀더 효과적이다.
    • reference attention_def3

  • vector z를 attention vector 혹은 weight vector라고 하고, z(i) = f(x(i), q).

    • z(i)는 기본적으로 scalar value
    • z(i)가 softmax 연산으로 정규화된 값을 a(i)라고 하자. vector a는 normalized attention vector라고 부르자.
    • a(i)는 보통 x(i)에 곱해져서 사용된다. 즉, x(i)가 q와의 관련도에 따라서 rescale 된다고 이해하면 편하다.
    • a(i) @ x(i) = x’(i)라고 하자. x'을 attended vector of x라고 하자.
      • @ : element-wise multiplication
    • d-dimension x(i)의 모든 element에 a(i)가 곱해져서 ‘broadcasted’라고 언급됨.
    • downstream application에서는
      • x’(i) 각각을 사용
      • 혹은 n개의 x’(i)를 더해서 하나의 d-dimension s를 사용
        • sentence embedding으로도 간주된다.
      • 혹은 사이즈가 n인 vector x’ 자체를 사용
        • attended vector of x w.r.t attention to q
    • reference attention_def2

tutorial

  • Memory,Attention,Sequence

    • attention 개념과 additive / multiplicative attention 관련 이미지가 인상적이다. 앞서 설명한 정의 부분과 비교해보면 이해하기 좋다. additive_multiplicative_attention

  • Attention in seq2seq

    • seq2seq model에서 attention은 decoder의 hidden state h(i-1)과 encoder의 hidden state e(j) 사이에서 정의된다. 그림을 보면 알겠지만, 일반적인 additive attention을 사용했다.

    • decoding 할 때, 입력 중 하나로 앞서 설명한 attended vector x’을 사용했다고 보면 된다.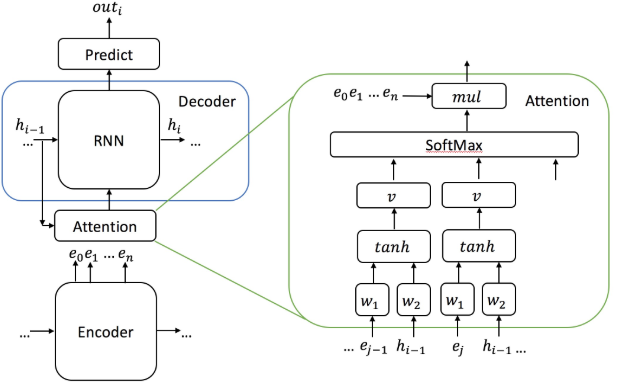

      seq2seq_attention_machanism

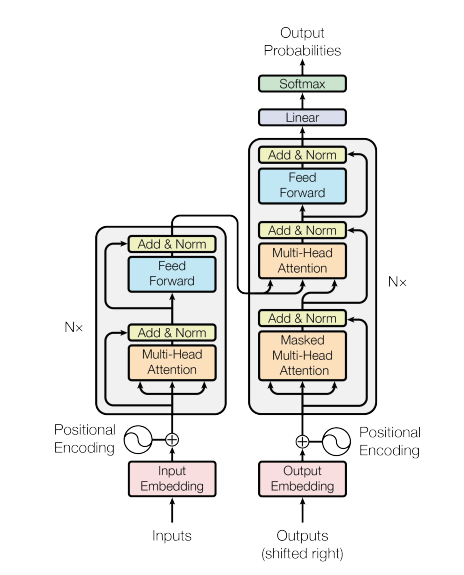
  • Transformer Attention is all you need

    scaled_dot_product_attention

    • Transformer에서 사용되는 수식은 앞서 설명한 것과는 약간 다르게 query, key, value 용어를 사용한다.
      • query <-> q
      • key <-> x vector(size m)
      • value <-> x vector(size m)
      • 앞서 설명한 용어와는 이와 같은 대응관계가 있다.
      • dot product attention을 계산할 때는 보통 학습대상 matrix를 곱해주는데, 그 결과값이 Q, K, V라고 생각 할 수 있다.
    • 보통 encoder, decoder hidden state sequence를 한번에 처리하는 것이 효과적이기 때문에, matrix연산으로 처리하려면 수식은 Q, K, V matrix를 사용하도록 변경된다(Q, K, V에 대응하는 W matrix가 있음). 입력(queries, keys, keys)에 W들을 적용해서 Q, K, V를 만드는데, 이걸 linear transformation을 적용한다고 언급했다. 실제 학습되는 대상도 대응하는 W matrix들이다. decoder timestep이 n, encoder timestep이 m이라고 하면 :
      • Q : n x dk
      • K : m x dk
      • V : m x dq
      • Q * K(T) / root(dk) : n x m, scaled
      • softmax(Q * K(T) / root(dk)) : n x m, row를 따라서 softmax
        • 각각의 q(in queries)에 대해서 row는 keys에 대한 attention 정도라고 간주하면 된다. 즉, 앞서 언급된 normalized attention vector라고 이해할 수 있다.
      • (softmax(Q * K(T) / root(dk))) * V : n x dq
        • normalized attention vector에 다시 keys를 곱해서 weight summation한 결과로 이해하면 편하다.
        • 이 결과는 이미 attention이 적용된 결과이므로 decoder hidden states(queries = n x dq)와 같은 길이를 갖는다.
        • 또한 이 결과는 keys를 압축한 각각의 q에 대한 context라고 간주 할 수 있으므로, 실제 사용할때는 q와 합쳐서(normalize 필요) downstream에 적용하는 기법을 사용한다.
    • 위와 같이 attention 연산은 Q, K, V matrix를 이용해서 한번에 계산되고 중간 결과물도 matrix로 유지된다. Transformer가 아니라 다른 모델에서도 실제 구현에서는 이런 방식을 취한다. 예를 들어, 앞서 attention 정의 부분에서 normalized attention vector a를 계산할 때를 생각해보자.
      • d-dimension q, vector x 전체에 대해 한번에 계산하면
        • a = softmax((W1 * x)(T) * (W2 * q)) : n x 1, column을 따라서 softmax
    • Transformer top-down explain
      • attention 계산 방법에 대해, 매우 자세하게 설명하고 있다.

  • Attention? Attention

    • attention 개념에 대한 자세한 설명. 아래 내용을 다 읽고 다시보면 좋다.

Self-Attention

why self-attention?

  • attention 정의를 살펴보면 score function f()의 파라미터는 x(i), q인데, 만약 q가 vector x에 있는 어떤 x(j)인 경우라면 어떨까? 이것은 vector x의 원소들 사이에서 어떤 연관성이 있는 지 계산하려고 할 때, 사용해볼만 할 것이다. 즉, d . ependency가 존재하는 경우라고 생각해도 된다. 따라서, 의미적으로 vector x 내부의 원소들 사이에서 정의되기 때문에 self-attention이라고 부른다.

    • score function : f(x(i), x(j))
    • vector x는 self-attention 적용 이후 vector x'으로 표현되는데, 이는 i에 따라서 전부 다르다. 따라서, time-variant라고 표현 가능하다.

  • 이런 경우와는 살짝 다르지만, q가 neural net에서 마지막 layer에 존재하는 변수인 경우가 있을 수 있다. 예를 들면, c-dimension q에 대해서 argmax(q)해서 가장 높은 값을 갖는 index를 최종 output class로 분류하는 분류기를 생각해 볼 수 있다. 이런 경우에 network에서 node q로 들어오는 입력이 n개의 node인 vector x라고 가정하자. 여기서 q와 vector x 사이의 attention을 계산한다면, 정의에 의해서 score function f(x(i), q)를 사용하면 될 것이다. 하지만, q는 vector x에서 index i가 변해도 고정된 변수이므로 score function에서 q를 생략해 볼 수도 있다. 이런 경우도 score function을 계산할 때, vector x만 관여되기 때문에 self-attention으로 간주할 수 있다.

    • score function : f(x(i))
    • vector x는 self-attention 적용 이후 vector x'으로 표현되는데, 이는 i에 따라서 전부 같다. 따라서, time-invariant라고 표현 가능하다.

  • 위와 같은 구분에 의해서 time-variant와 time-invariant라고 명명하고 관련된 논문을 정리해봤다.

time-variant

  • paper

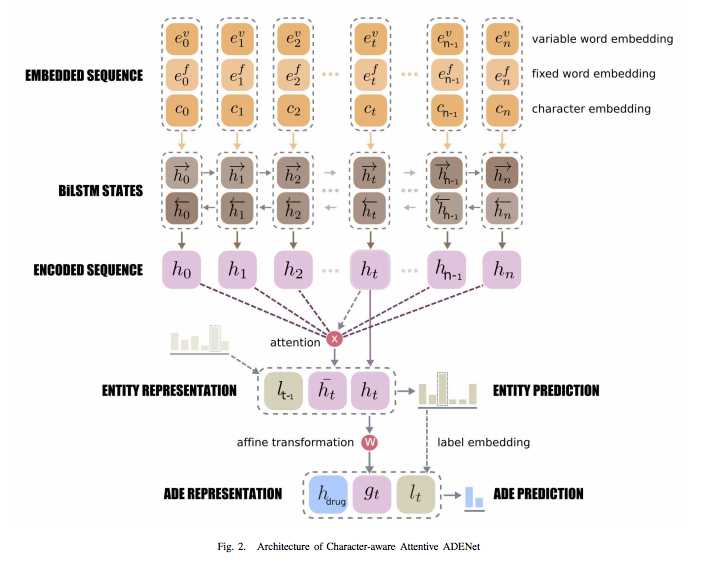
    • An Attentive Sequence Model for Adverse Drug Event Extraction from Biomedical Text self_attention

      • NLP 문제에서 전형적인 sequence labeling 문제를 해결 할때, LSTM 등을 사용하는데, 여기서는
        • LSTM 위에 attention layer를 올리고 LSTM의 hidden state와 attended vector를 summation한 결과, 그리고 이전 timestep에서 결정된 label을 feature로 사용해서 최종 label을 결정하는 네트웍을 구성했다. 여기서 attended vector는 timestep에 따라 전부 다르게 나오게 된다. 직관적으로 생각해도, 현재 i번째 token의 label을 결정할 때, j번째 token의 영향이 매우 컸다고 할지라도, (i+1)번째 token의 label을 결정할때는 j번째 token의 영향은 크지 않을수도 있으니 token별로 attended vector가 다르게 나온다는 것은 매우 합리적인 생각일 것이다.

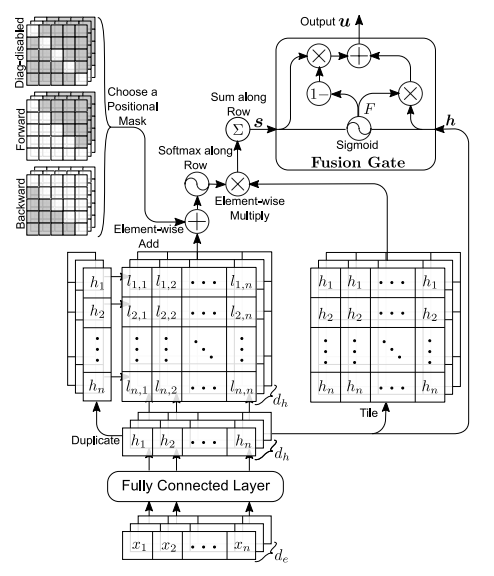
    • DiSAN: Directional Self-Attention Network for RNN/CNN-Free Language Understanding multi_dimensional_self_attention

      • 앞서 'mathematical definition'에서 참조한, 중요한 논문이다.
      • 그림을 보면 hidden state vector h에 대한 self-attention matrix가 만들어지는 모습을 볼 수 있다.
        • 여기서 착각하지 말아야 할 부분은, matrix의 개별 요소는 scalar 값이라는 점이다. similarity matrix라고도 부른다.

    • Attention Is All You Need transformer_model

      • Transformer의 구조를 보면, encoder/decoder 부분에서 self-attention을 여러층으로 쌓아서 사용하는 것을 볼 수 있다. 기존에 LSTM/GRU 등을 이용해서 context를 참조하던 방식은 현재 timestep에서 이전 timestep의 계산이 끝날 때까지 기다려야하는 문제가 있어서, 속도가 느린 문제가 있다. 이런 문제를 해결하기 위해서 attention machenism을 이용해서 RNN-free 구조로 변경하는 것이 논문의 핵심이라고 할 수 있다. 물론, 기존 RNN 정도의 성능을 보이려면 attention을 여러 layer로 쌓아야하고 temporal information을 다르게 하기 위해서 positional encoding을 추가해서 사용해야하지만, RNN과는 다르게 병렬처리가 가능하기 때문에 매우 빠른 학습이 가능하다.

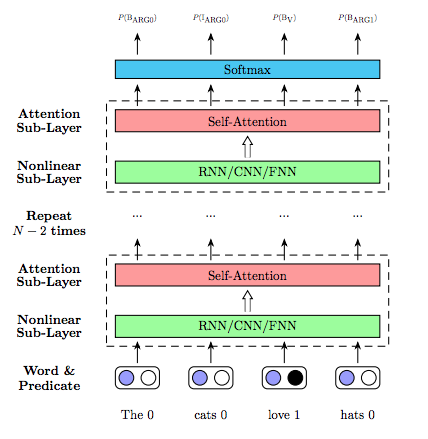
    • Deep Semantic Role Labeling with Self-Attention self_attention_with_fnn

      • Transformer 모델은 번역을 위해서 만들어졌지만, 이 논문처럼 sequence labeling 문제를 위해서도 사용 가능하다. 차용한 부분은 Transformer의 encoder 부분에서 사용된 multi-headed self-attention 기법인데, LSTM을 대체하기 위해서 'FNN + self-attention with positional encoding' block을 10개 정도 쌓아 올렸다. LSTM이 조금 느리긴 하지만, single layer로도 훌륭한 성능을 보인다는 것이 역으로 증명되는 케이스라고 할 수 있다.

    • Reinforced Mnemonic Reader for Machine Reading Comprehension

      • 지금까지는 sequence labeling, translation 등에서 사용되는 attention을 살펴봤는데, 이 논문에서는 machine reading comprehension에서 사용되는 attention에 대해 잘 설명하고 있다.
      • self-attention에서 사용되는 attention function
        • multiplicative attention
        • f(v,u) = relu(W1 * v)(T) * relu(W2 * u) : scalar value
          • W1, W2 : p x 2d (p는 임의의 dimension 값)
        • V, U vector의 모든 원소 v,u에 대해서 f(v,u)를 계산한 결과 : n x m similarity matrix E
          • 한번에 E를 계산하는 수식도 원소 v,u간 계산하는 수식과 똑같다.
          • E = relu(W1 * V)(T) * relu(W2 * U) : n x m matrix

time-invariant

  • paper

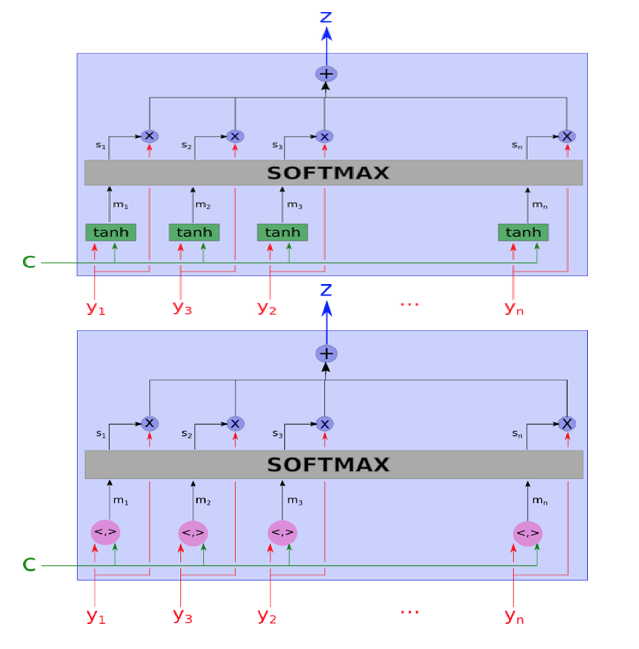
    • FEED-FORWARD NETWORKS WITH ATTENTION CAN SOLVE SOME LONG-TERM MEMORY PROBLEMS

      • 그림을 보면 input vector에 대해 time-invariant attention을 구해서, 단순하게 rescaling을 해서 합쳤다는 것을 알 수 있다. 구조는 단순하지만, input vector를 그냥 사용하는 것보다는 성능 개선 효과가 있다.

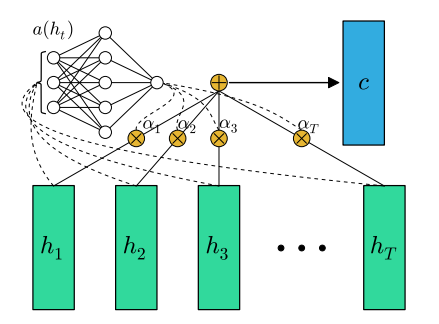
      time_invariant_self_attention

    • Neural Architectures for Fine-grained Entity Type Classification

      • 바로 위 모델과 거의 유사한데, sequence labeling 문제에서 time-invariant attention을 사용했다고 생각하면 된다.

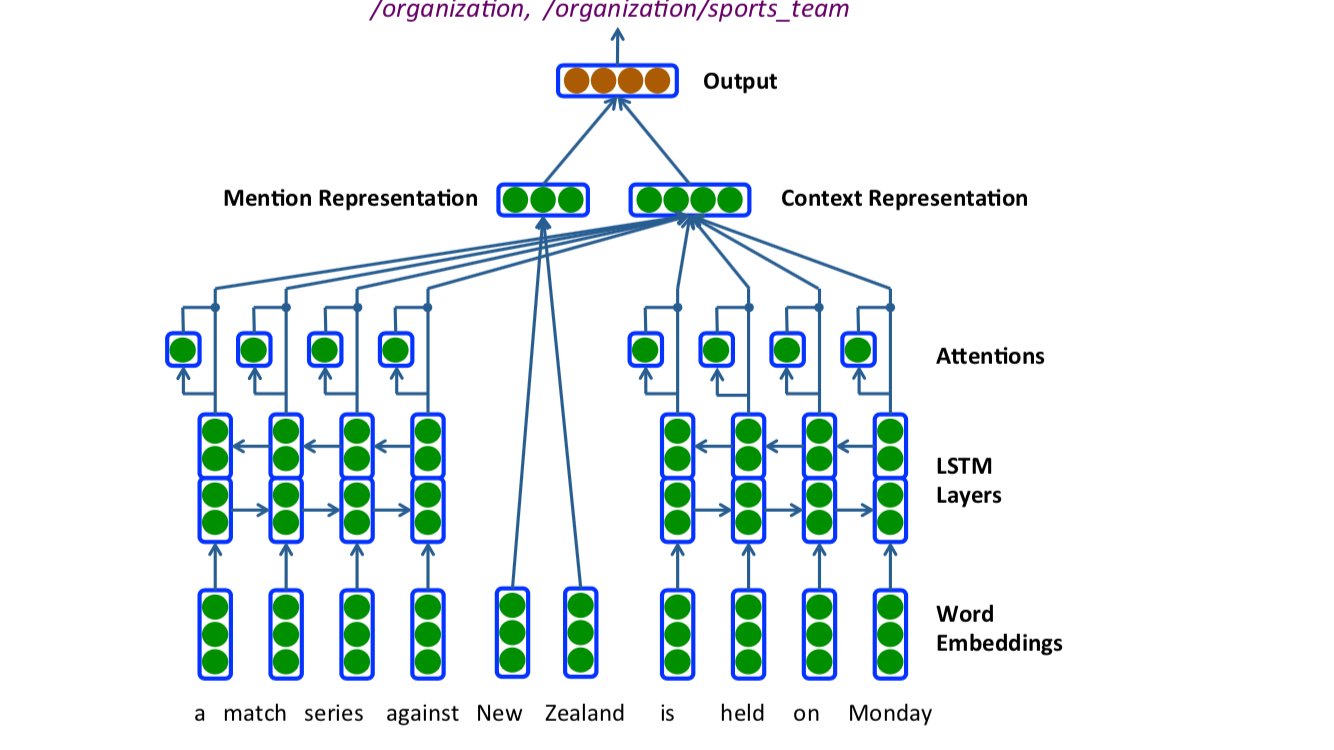
      ner_attention

    • A STRUCTURED SELF-ATTENTIVE SENTENCE EMBEDDING

      • 이 논문에서는 sentence embedding을 계산할 때, time-invariant self-attention을 사용했는데, 다른 점이라면 multi-headed attention을 사용해서 input vector를 다양한 관점에서 attention을 바꿔가면서 sentence embedding을 만들었다는 것이다. 또한 여러개의 attention을 사용했기 때문에, 서로 다른 attention이 동일한 부분에 attention(attention-redundancy) 되지 않도록 하는 regularization 기법을 사용한 것도 주목할 만하다.

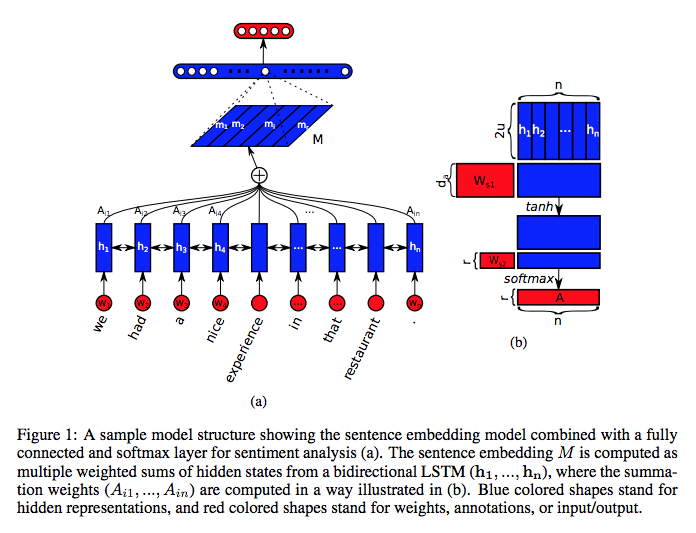
      multi_head_self_attention

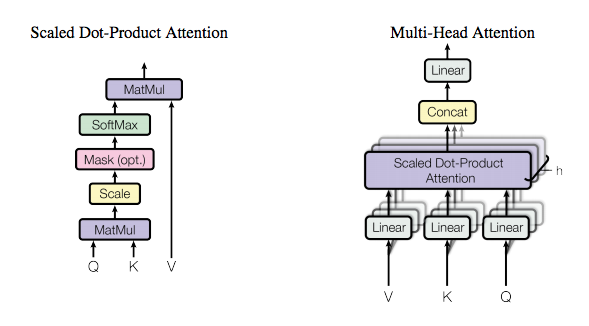
Multi-Headed Attention

  • Transformer를 언급하면서 자주 나왔던 attention이 multi-headed일 것이다. 복잡한 것은 아니고, attention을 여러개 사용했다고 보면 된다. 여기서 encoder/decoder 단에서 self-attention은 multi-headed self-attention으로 이해하면 된다. encoder/decoder에서 self-attention은 같은 입력 embedding vector 3개에 linear transformation matrix W들을 적용해서 Q, K, V를 만든다. decoder에서 seq2seq 방식의 attention에서는 Q만 decoder의 입력을 이용해서 만들고 K, V는 encoder의 입력을 이용하도록 구현한다. 학습은 linear transformation 역할을 하는 matrix W들의 weight가 변하는 것으로 수행된다고 할 수 있다. single-headed attention와 비교해서 계산 속도가 느리다고 생각 할 수 있지만, 8개 attention에서 linear transformation의 dimension이 1/8로 맞춰뒀기 때문에 전체적인 계산량은 비슷하다고 보면 된다.

  • 실제 코드

    • 구현 코드를 보면, 이론과는 다르게 3개의 matrix W만 있고, linear transformation 결과를 spilt해서(사실은 reshape, transpose) 각각의 head별로 softmax 해준다는 점에서 single-headed와 차이가 생긴다는 점을 알 수 있다.
    • 또한 마지막에 W_o를 가지고 model dimension을 맞춰주는 부분이 있는데, 만약 head가 1개라면 이 부분에서 single-headed attention과 multi-headed(head=1)과 차이가 생긴다고 볼 수 있다. 즉, 학습되는 matrix의 수에서 차이가 생김.

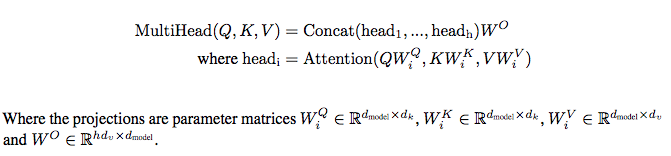
multi_headed_attention_1 multi_headed_attention_2

Multi-Dimensional Attention

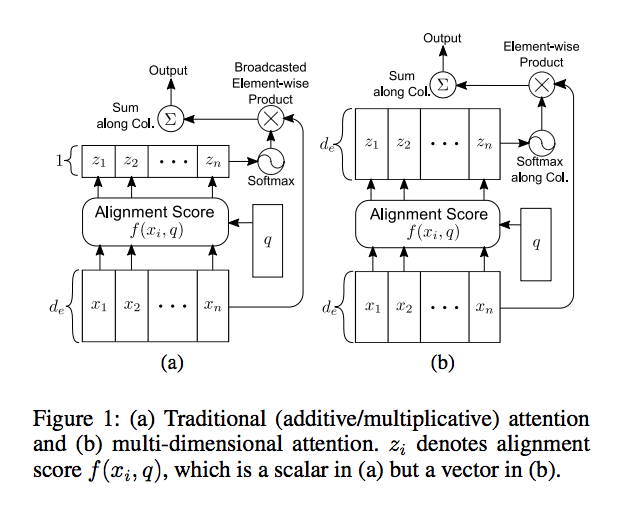
  • 'mathematical definition'에서 참조한 논문에서 나온 attention이다. 일반적으로 attention을 계산할 때, 빠지지 않는 연산이 softmax라고 할 수 있다. attention vector z에 대해 softmax한 결과가 normalized attention vector a라고 하면, a(i)와 d-dimension x(i)가 곱해져서 x'(i)로 rescaled된다. 즉, x(i)의 모든 요소에 대해서 동일하게 a(i) scalar 값이 곱해진다. 그런데 약간 생각을 달리해서 d-dimension x(i)의 개별 요소를 feature라고 간주하면 서로 다른 모든 feature에 동일한 weight를 곱하는 것보다는 feature별로 다른 weight를 곱하는 것이 좀더 합리적일 것이라는 가정을 할 수 있을 것이다. 이런 개념이 적용된 attention이 바로 multi-dimensional attention이다. 아래 그림에서 확인 할 수 있는 것처럼, z는 vector가 아니라 d x n matrix로 계산되고, 개별 feature에 해당하는 row별로 softmax한 결과가 x(i)의 해당 feature에 곱해진다.

attention_def2

Re-Attention

  • re-attention은 앞서 기술한 여러가지 attention 기법과는 결을 달리하는 attention 기법이다. 이는 attention layer를 여러 층을 쌓아서 attention을 계속 반복하면 문제 해결에 적합한 입력으로 attention이 정제된다는 가정에서 출발한다. 마치 CNN에서 layer를 계속 통과하면서 문제 해결을 위해 feature가 추상화되는 과정과도 어느정도 유사하다고 볼 수 있다.

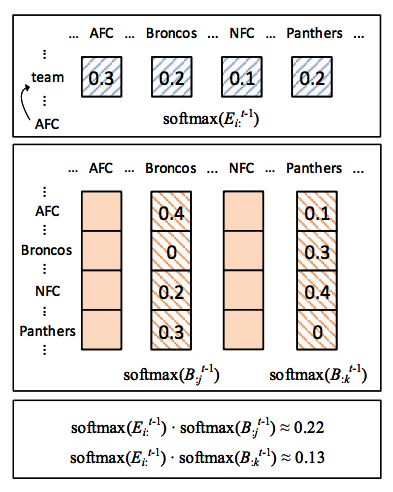
  • 아래 그림에서 보면, 이전 t-1 layer에서 계산된 similarity matrix를 가지고 계산한 값을 현재 t layer의 attention을 계산할 때 더해주는 부분을 볼 수 있는데, 이 부분이 re-attention이다.

  • layer를 쌓으면서 attention을 반복하면 생길 수 있는 문제는 반복해도 별 차이가 안생기는 attention redundancy와 반복하면서 attention을 잃어버리는 attention deficiency라고 볼 수 있는데, 이 논문에서는 이 문제를 효과적으로 처리했다고 강조하고 있다.

re_attention_1 re_attention_2

Etc