[HMM] Hidden Markov Model 구현 관점에서 - dsindex/blog GitHub Wiki

HMM에 대해 어느정도 이해를 했다면 구현관점에서 접근할 필요가 생긴다. 이 자료는 그럼 면에서 아주 가치있다고 볼 수 있다.

hmm 1

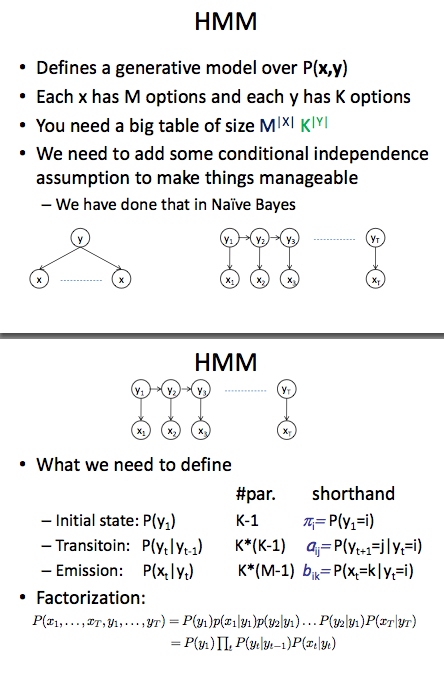
HMM을 구현하기 위해서 학습데이터로부터 계산해야할 확률값들은 위에 잘 표현되어 있다. 전체 상태의 수가 K개, 전체 심벌의 수가 M개라고 하면, 확률값을 저장하기 위해 (K + K^2 + K*M)개의 확률을 저장할 공간이 필요하다. (위에서 K-1로 했는데, K-1개를 알면 나머지 1개는 1에서 빼면 되기 때문이다. 여기서는 편의상 K로 계산)

hmm 2

이러한 확률값을 구하는 방법은 fully observed training data라면 단순히 카운트해서 normalization을 해주면 될것이고, state가 hidden되어 있다면(즉, unsupervised라면) Expectation Maximization 알고리즘을 사용해서 추정해줘야한다. 일반적으로 POS tagging, NP/VP chunking, NER(Named Entity Recognition) 등의 sequential tagging 문제를 다룰 때는 label(tag)이 있는 학습데이터가 이미 있다고 가정하고 들어가기 때문에 EM을 사용하지 않는다. 따라서, 학습데이터로부터 이미 계산된 확률값이 있다고 가정하고 주어진 symbol sequence가 있을 때, 가장 그럴듯한 state sequence를 찾으려면 어떤 수식을 사용해야하는지, 또 어떻게 구현해야 하는지 알아보자.

hmm 3

사실 이 자료에서 설명하는 forward variable alpha, backward variable beta는 most probable state sequence를 계산하는데 관여하지 않는다. 단지 P(y(t) = k | X), 즉 symbol sequence X가 있을 때, time=t에서 상태가 'k'일 확률을 계산할때나 필요하다. 즉, HMM model을 evaluation할 때 관여하는 변수라는 것이다. 따라서, most probable state sequence를 찾을 때는 아래 수식만 주목하면 된다. 이것은 일반적으로 Viterbi Algorithm을 이용해서 계산한다.

hmm 4

위 수식이 이해하기 어려우면 다음 그림을 보자.

hmm 5

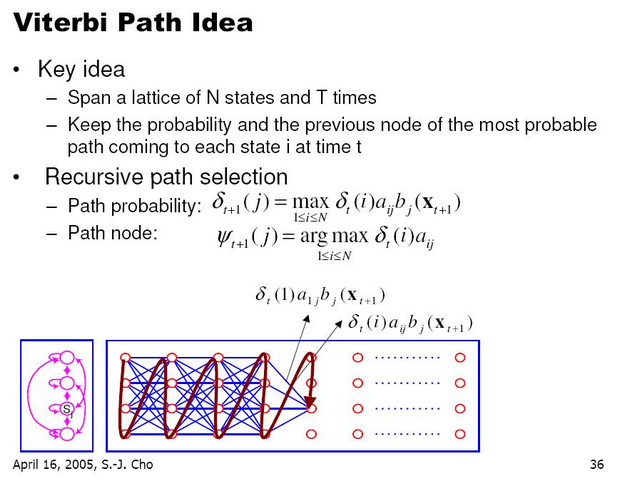
이 그림에서 나오는 deta값은 path probability인데 위에서 설명하는 V값과 같은 내용이다.

  1. 시간 t에서의 상태에서 시간 t+1로의 상태로 전이확률 a(i,j)
  2. 시간 t+1 상태 j에서 output symbol emission 확률 b(j, x(t+1))

이 두개의 곱이 최대가 되는 path의 확률을 의미한다.

이제 Viterbi Algorithm을 적용하기 위해서, 주어진 입력(symbol sequence)에 대해 trellis를 만들고 V값을 순차적으로 계산하면서 시간 1에서 시간 T까지 진행한다. 시간 1에서 V(1)값은 alpha값과 같다. 즉, 상태의 수 K개만큼 나온다.

V(1,1) = P(x1 | y1=1) * py(1)
....
V(1,K) = P(x1 | y1 = K) * py(K)

여기서 py(i)는 initial state probability. 시간 2에서 V(2)값은 앞에서 계산된 V(1)값을 이용해서 계산한다.

V(2,1) = P(x2 | y2=1) * max { a(i,1) * V(1,1) }  for all i=1...K
....
V(2,K) = P(x2 | y2=K) * max { a(i, 2) * V(1,K) } for all i=1...K

이것 역시 상태의 수 K개만큼 나온다.

hmm 6

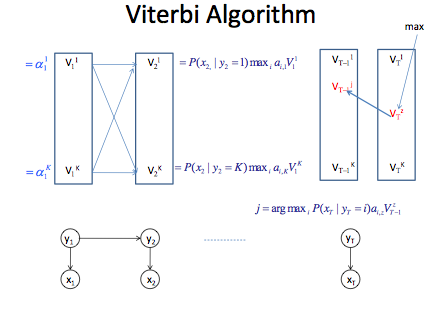
시간 T까지 진행하면 V(1), V(2), ..., V(T)는 전부 합쳐서 TK 개가 저장될 것이다. 임의의 시간 t에서만 보면, max 연산을 수행하기 위해서 for loop를 K개 만큼 돌아야한다. 그렇다면 time complexity도 O(TK^2)이 된다. 속도를 중시한다면 V(2)를 계산 할때, V(1)에서 어떤 임계값 이하는 사용하지 않는 방법도 있다. (pruning technique)

hmm 7

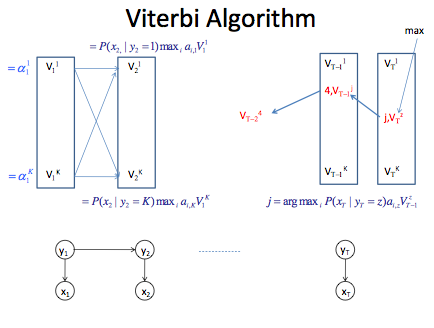
마지막 시간 T까지 왔을 때, 모든 패스들 중에서 가장 확률이 높은 패스는 backtracking을 해서 계산해야한다.

  1. 시간 T에서 가장 높은 확률값을 갖는 V(T,2)를 선택한다.
  • 예를 들어, state yT=2에서 가장 높은 확률값을 가진다고 하자. (설명의 편의를 위해서)
  1. V(T,2)를 계산할 때 max 연산을 했는데, 최대가 되는 index i값도 별도로 저장해 둬야한다.
  • 이것이 path node이다.
  • path node는 path probability에서 destination의 output 확률을 제거하고, 그 확률이 최대가 되는 이전 상태이다. 현재 어떤 output이 있는 지 고려하지 않고 계산한다. 그 이유는 최대가 되는 이전 상태를 계산할때 현재 output은 모두 동일하기 때문이다.
  1. V(T,2)의 path node가 j라면 해당하는 이전 시간 T-1로 backtracking한다.
  2. V(T-1, j)의 path node가 4라면 해당하는 이전 시간 T-2로 backtracking한다.
  3. 이런식으로 시간 1까지 backtracking하면 most probable state sequence가 계산된다.

위에서 언급한 path node까지 고려한 space complexity는 TK2가 될 것이고, time complexity는 그대로이다. V값을 계산할 때, 확률은 0~1 사이 값이므로 곱했을 때, 매우 작아질 수 있다. 따라서, 구현시에는 log값을 취해서 계산하는 트릭을 사용한다.