1 Page Cheat Sheet - dohdat/leetcode-practice GitHub Wiki

Sort hashmap by value

const mapSort1 = new Map([...myMap.entries()].sort((a, b) => b[1] - a[1]));
console.log(mapSort1);

// Map(4) {"c" => 4, "a" => 3, "d" => 2, "b" => 1}

Indegree && Outdegree

var findJudge = function(n, trust) {
  let trustCounts = new Array(n + 1).fill(0);
  for (let [a, b] of trust) {
    trustCounts[a]--;
    trustCounts[b]++;
  }
  for (let i = 1; i < trustCounts.length; i++) {
    if (trustCounts[i] === n - 1) {
      return i;
    }
  }
  return -1;
};

Shortest Path:

Find the shortest path from k to n

Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2

Output: 2

Dijkstra (weighted)

  var networkDelayTime = function (times, n, k) {

    
    // Our return value, how long did it take
    // to reach all nodes within the network from {k}
    let time_taken = 0;

    // A set so we don't visit the same node twice.
    const visited_set = new Set();

    const min_heap = new MinPriorityQueue();

    // An adjacency list, where we store 
    // Node -> [[Edge, Cost],[Edge, Cost]]
    const node_edge_cost = new Map();

    // Build the adjacency list.
    for (const [node, edge, cost] of times) {
        let edges = [];
        if (node_edge_cost.has(node)) {
            edges = node_edge_cost.get(node);
        }
        edges.push([edge, cost]);
        node_edge_cost.set(node, edges);
    }

    // We have been asked to start at {k}
    // So we enqueue {k} at the cost of 0, as of course
    // it costs nothing as we start here.
    min_heap.enqueue([k, 0], 0);

    while (min_heap.size()) {

        // Get the cheapest operation relative to {k}
        // Node and cost
        const [node, cost] = min_heap.dequeue().element;

        // Have we already been here? No loops today kiddo
        if (visited_set.has(node)) continue;

        // Set it. We don't want to come back here. 
        visited_set.add(node);

        // Did our distance increase?
        // If so, update it. If not, keep the same
        time_taken = Math.max(cost, time_taken);

        // Get the edges for this node (If any)
        const node_edges = node_edge_cost.get(node) || [];

        for (const [edge_node, edge_cost] of node_edges) {
            if (!visited_set.has(edge_node)) {
                
                // Add it to the queue, set the priority to the cost of the edge
                // So we only ever visit the cheapest edge.
                min_heap.enqueue([edge_node, edge_cost + cost], edge_cost + cost);
            }
        }
    }

    // Did we visit every node?
    // If not, we failed to spread the message across the network.
    // If so, return the time taken. 
    return visited_set.size === n ? time_taken : -1;
};

Time Complexity: O(E log V)

Bellman Ford

Works when there is negative weight edge. Slower than Dijkstra.

var networkDelayTime = function(times, n, k) {
  let arr = new Array(n + 1).fill(Infinity);
  arr[k] = 0;
  for (let i = 0; i <= n; i++) {
    let temp = arr.slice();
    for (let [source, target, cost] of times) {
      if (temp[source] === Infinity) continue;
      temp[target] = Math.min(temp[target], temp[source] + cost);
    }
    arr = temp;
  }
  arr.shift();
  let res = Math.max(...arr);
  return res === Infinity ? -1 : res;
};

Time Complexity: O ( V ⋅ E )

All paths from Source to Target:

Find all possible paths from source to target. Return them in any order.

Input: graph = [[1,2],[3],[3],[]]

Output: [[0,1,3],[0,2,3]]

Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

var allPathsSourceTarget = function(graph) {
  let res = [];
  let target = graph.length - 1;
  function dfs(node, path) {
    path.push(node);
    if (node === target) {
      res.push(path);
      return;
    }

    let visiting = graph[node];
    for(let cur of visiting) {
      dfs(cur, [...path])
    }
  }

  dfs(0, []);
  return res;
};

Topological Sort (Cycle Detection):

Return the correct order you should take to finish all courses.

Input: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]

Output: [0,2,1,3]

Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0. So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3].

var findOrder = function(numCourses, prerequisites) {
  let preMap = new Map();
  //Create a set, not an array, so that we do not add visited nodes
  let res = new Set();
  let visited = new Set();
  //create adjList 
  for (let [crs, pre] of prerequisites) {
    preMap.set(crs, (preMap.get(crs) || []).concat(pre));
  }
    

  function dfs(node) {
    if (visited.has(node)) return false;
    visited.add(node);
    let visiting = preMap.get(node);
    while (visiting && visiting.length > 0) {
      let c = visiting.shift();
      if (!dfs(c)) return false;
    }
    visited.delete(node);
    res.add(node);
    return true;
  }

  for (let i = 0; i < numCourses; i++) {
    if (!dfs(i)) return [];
  }
  return [...res];
};

Time Complexity: O(V+E), where V = vertices, E = Edges.

Union Find (Disjoint Set):

A Union-Find data structure is to maintain a set of elements partitioned into a number of mutually disjoint (non-overlapping) subsets. So no elements belong to more than one set.

Applications:

connected component in Graph problem.
detecting cycles in graph.
minimum spanning tree.

Question:

Find if Path Exists in Graph

Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2

Output: true

var validPath = function(n, edges, source, destination) {
  let parent = new Array(n);
  for (let i = 0; i < parent.length; i++) {
    parent[i] = i;
  }

  function find(a) {
    while (parent[a] !== a) {
      parent[a] = parent[parent[a]];
      a = parent[a];
    }
    return a;
  }

  function union(a, b) {
    const rootA = find(a);
    const rootB = find(b);
    if (rootA !== rootB) {
      parent[rootA] = rootB;
    }
  }

  for (let [a, b] of edges) {
    union(a, b);
  }

  return find(source) === find(destination);
};

Time Complexity: O(log n)

Intervals:

Given an array of intervals where intervals[i] = [starti, endi], merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input.

Input: intervals = [[1,3],[2,6],[8,10],[15,18]]

Output: [[1,6],[8,10],[15,18]]

Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6].

var merge = function(intervals) {
    intervals.sort((a, b) => a[0] - b[0]);
    let prev = intervals[0];
    let res = [prev];
    for (let i = 0; i < intervals.length; i++) {
        let c = intervals[i];
        if (c[0] <= prev[1]) {
            prev[1] = Math.max(prev[1], c[1]);
        } else {
            res.push(c);
            prev = c;
        }
    }
    return res;
};

Fast & slow pointers:

Return true if there is a cycle in the linked list. Otherwise, return false.

Input: head = [3,2,0,-4], pos = 1

Output: true

Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

var hasCycle = function(head) {
  let slow = head;
  let fast = head;
  while (fast && fast.next) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow === fast) return true;
  }
  return false;
};

Heap (Priority Queue):

Heaps are structures meant to allow quick access to the min or the max. Can get acccess to max or min at constant time O(1)

Time complexity: O(nlogn)

MaxPriorityQueue

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.

Input: nums = [1,1,1,2,2,3], k = 2

Output: [1,2]

var topKFrequent = function(nums, k) {
  let map = new Map();
  let maxHeap = new MaxPriorityQueue(item => item.value);

  // O(n) Time complexity
  for (let num of nums) {
    map.set(num, (map.get(num) || 0) + 1);
  }

  let ans = [];
  // We are building a maxHeap for the D unique item
  // O(D) time complexity
  for (let [key, value] of map) {
    maxHeap.enqueue(key, value);
  }

  for (let i = 0; i < k; i++) {
    // We are dequeuing the k elements which can take upto O(klogD)
    let _item = maxHeap.dequeue();
    ans.push(_item.element);
  }

  return ans;
};

Longest Common Subsequence

Input: text1 = "abcde", text2 = "ace"

Output: 3

Explanation: The longest common subsequence is "ace" and its length is 3.

var longestCommonSubsequence = function(text1, text2) {
  const memo = new Map();
  function recursion(index1, index2) {
    // base cases
    if (index1 < 0 || index2 < 0) return 0;

    const key = index1 + "#" + index2;

    if (memo.has(key)) return memo.get(key);

    let result = 0;
    if (text1[index1] === text2[index2]) {
      result = recursion(index1 - 1, index2 - 1) + 1;
    } else {
      result = Math.max(
        recursion(index1, index2 - 1),
        recursion(index1 - 1, index2)
      );
    }

    memo.set(key, result);
    return result;
  }
  return recursion(text1.length - 1, text2.length - 1);
};

Backtracking:

Permutations

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

Input: nums = [1,2,3]

Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

var permute = function(nums) {
  let res = [];
  let cur = new Set();
  function backtrack() {
    if (cur.size === nums.length) {
      res.push([...cur]);
      return;
    }

    for (let n of nums) {
      if (cur.has(n)) {
        continue;
      }
      cur.add(n);
      backtrack();
      cur.delete(n);
    }
  }
  backtrack();
  return res;
};

Combinations

No Duplicates

Input: n = 4, k = 2

Output: [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]

var combine = function(n, k) {
  let res = [];
  let cur = new Set();
  function backtrack(index) {
    if (cur.size === k) {
      res.push([...cur]);
      return;
    }
    for (let i = index; i <= n; i++) {
      if (cur.has(i)) {
        continue;
      }
      cur.add(i);
      backtrack(i + 1);
      cur.delete(i);
    }
  }
  backtrack(1);
  return res;
};

Sliding Window:

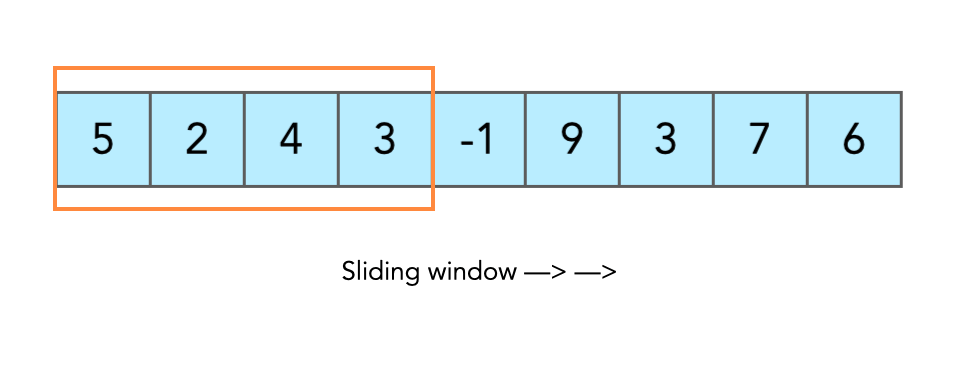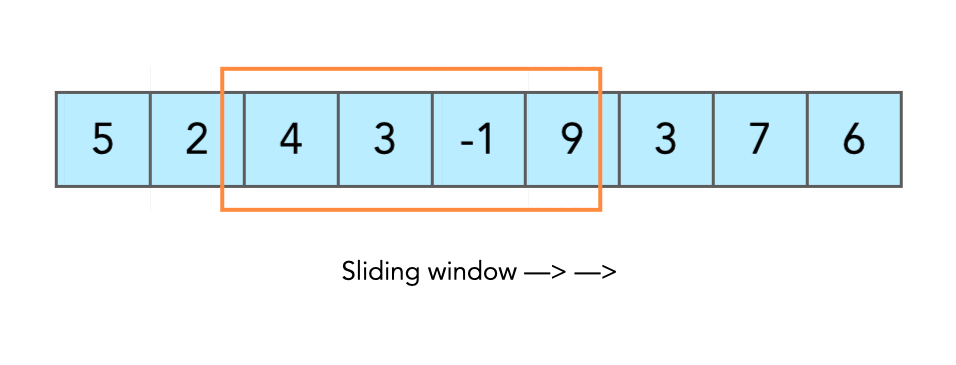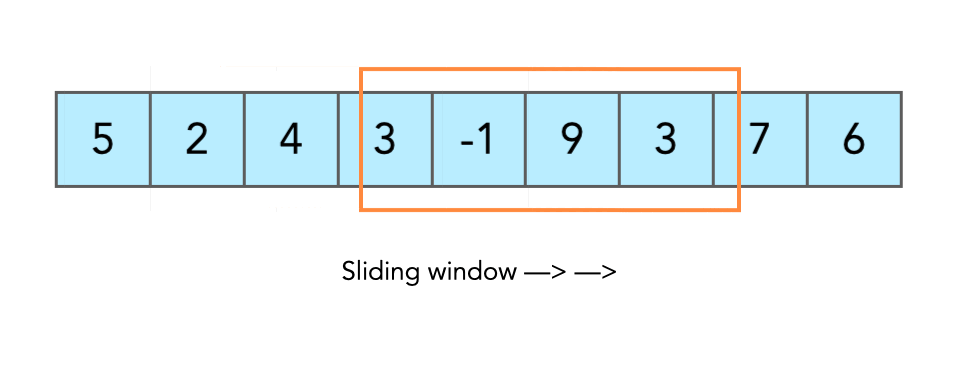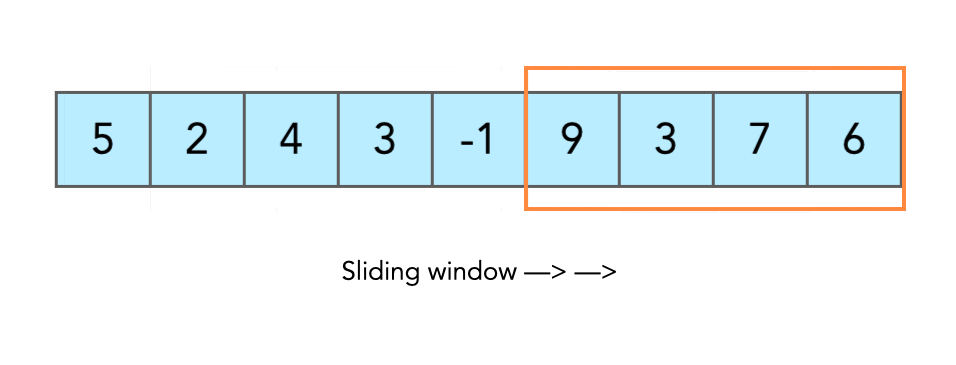
Given a string s, find the length of the longest substring without repeating characters.

Input: s = "abcabcbb"

Output: 3

Explanation: The answer is "abc", with the length of 3.

var lengthOfLongestSubstring = function(s) {
    let set = new Set();
    let max = 0;
    let left = 0;
    for (let right = 0; right < s.length; right++) {
        while (set.has(s[right])) {
            set.delete(s[left++]);
        }
        set.add(s[right]);
        max = Math.max(max, right - left + 1);
    }
    return max;
};

Stack:

Question:

Decode this string.

Input: s = "3[a]2[bc]"

Output: "aaabcbc"

const decodeString = s => {
  const stack = [];
  for (const char of s) {
    if (char !== "]") { stack.push(char); continue; }
    let cur = stack.pop();
    let str = '';
    while (cur !== '[') {
      str = cur + str;
      cur = stack.pop();
    }
    let num = '';
    cur = stack.pop();
    while (!Number.isNaN(Number(cur))) {
      num = cur + num;
      cur = stack.pop();
    }
    stack.push(cur);
    stack.push(str.repeat(Number(num)));
  }
  return stack.join('');
};

Two Pointers:

Return the maximum amount of water a container can store.

Input: height = [1,8,6,2,5,4,8,3,7]

Output: 49

Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

var maxArea = function(height) {
  let left = 0;
  let right = height.length - 1;
  let max = 0;
  while (left <= right) {
    let curArea = Math.min(height[left], height[right]) * (right - left);
    if (height[left] <= height[right]) {
      left++;
    } else {
      right--;
    }
    max = Math.max(max, curArea);
  }
  return max;
};

BFS:

Iterative

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Input: root = [3,9,20,null,null,15,7]

Output: [[3],[9,20],[15,7]]

var levelOrder = function(root) {
    if(!root) return [];
    let q = [root];
    let res = [];
    while (q.length !== 0) {
        let temp = [];
        let len = q.length;
        for (let i = 0; i < len; i++) {
            let c = q.shift();
            temp.push(c.val);
            c.left && q.push(c.left);
            c.right && q.push(c.right);
        }
        res.push(temp);
    }
    return res;
};

DFS:

In-order:

Left-> Root -> Right

Pre-order:

Root-> Left -> Right

Post-order:

Left-> Right -> Root

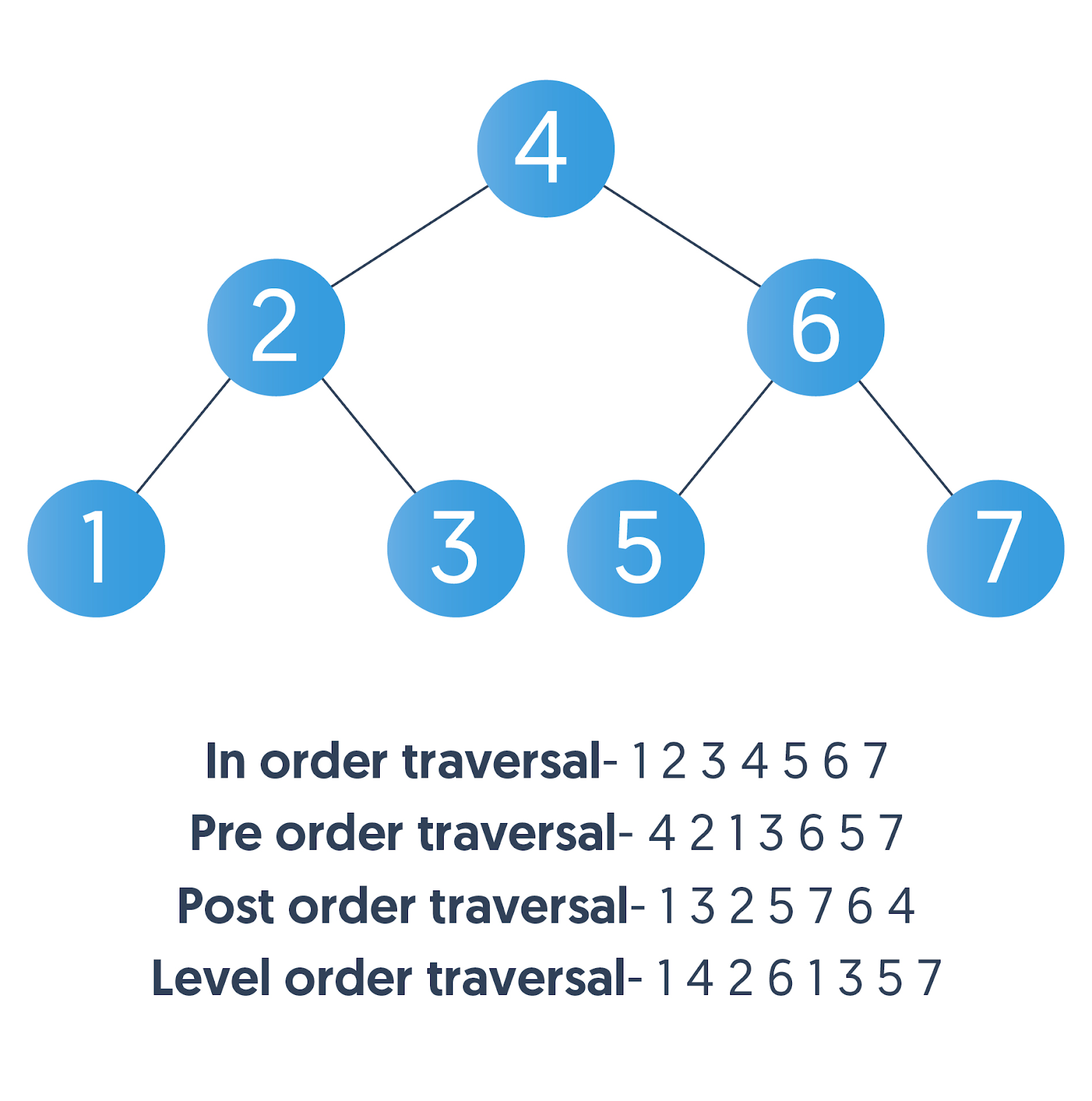
Question:

Given the root of a binary tree, return the inorder traversal of its nodes' values.

Input: root = [1,null,2,3]

Output: [1,3,2]

var minDiffInBST = function(root) {
  let min = 0;
  let res = [];
  function dfs(node) {
    if (!node) return false;
    node.left && dfs(node.left);
    res.push(node.val);
    node.right && dfs(node.right);
  }
  dfs(root);
  return min;
};

Question:

Find the number of islands in a grid.

Output: 3

var numIslands = function(grid) {
    let rows = grid.length;
    let cols = grid[0].length;
    let res = 0;
    function dfs(r, c) {
        if (r < 0 || c < 0 || r >= rows || c >= cols || !grid[r][c] || grid[r][c] === '0') {
            return;
        }
        grid[r][c] = '0';
        dfs(r - 1, c);
        dfs(r + 1, c);
        dfs(r, c - 1);
        dfs(r, c + 1);
    }
    for (let r = 0; r < rows; r++) {
        for (let c = 0; c < cols; c++) {
            if (grid[r][c] === '1') {
                res++;
                dfs(r, c);
            }
        }
    }
    return res;
};

Binary Search:

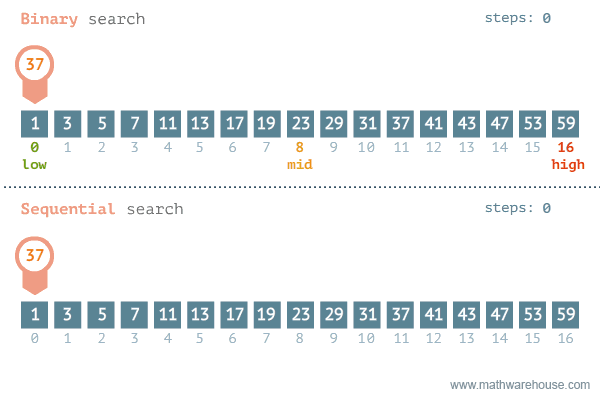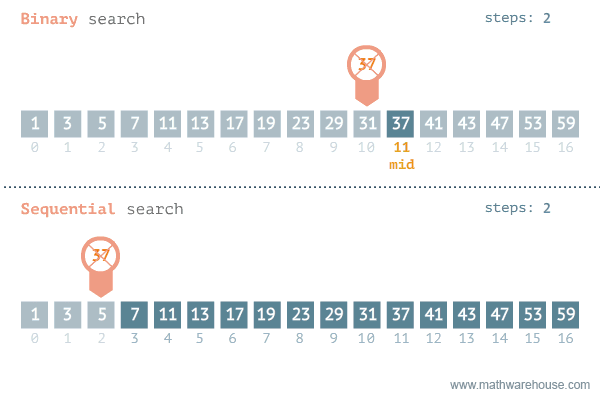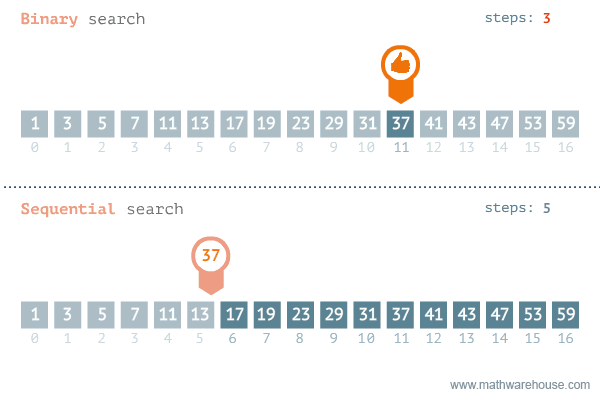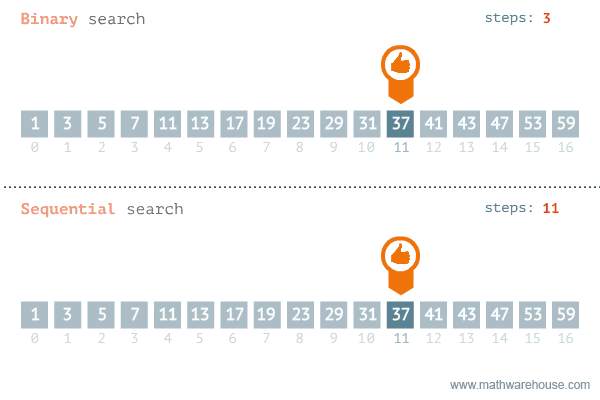
Find if target exists in array. You must write an algorithm with O(log n) time complexity.

Input: nums = [-1,0,3,5,9,12], target = 9

Output: 4

Explanation: 9 exists in nums and its index is 4

var search = function(nums, target) {
  let left = 0;
  let right = nums.length - 1;
  while (left <= right) {
    let mid = Math.floor((right + left) / 2);
    if (nums[mid] === target) {
      return mid;
    }
    if (nums[mid] > target) {
      right = mid - 1;
    } else {
      left = mid + 1;
    }
  }
  return -1;
};

Linked list cycle

var hasCycle = function(head) {
  let slow = head;
  let fast = head;
  while (fast && fast.next) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow === fast) return true;
  }
  return false;
};

Reverse a linked list

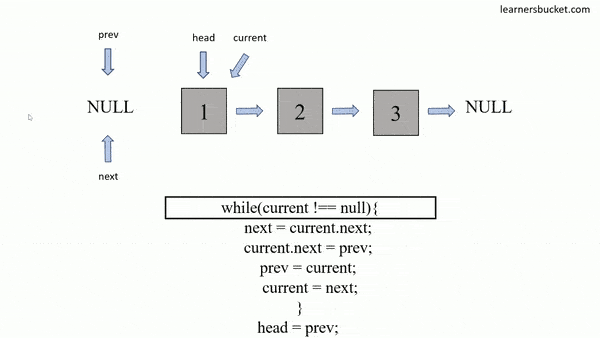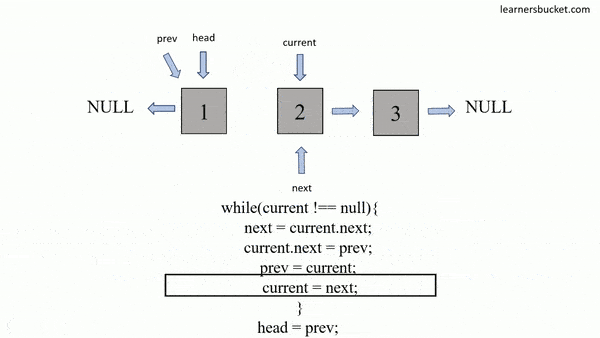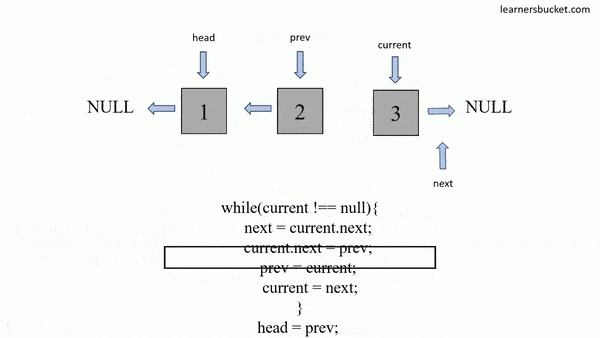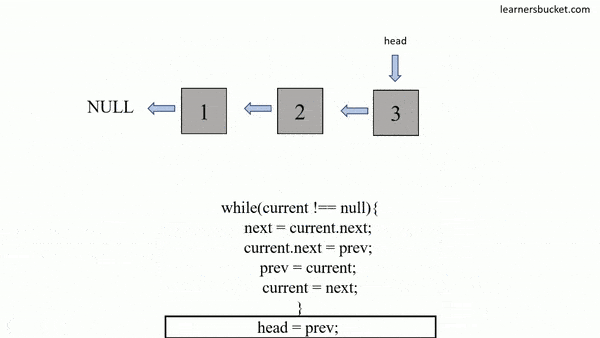
var reverseList = function(head) {
  let prev = null;
  let cur = head;
  while (cur) {
    [cur.next, prev, cur] = [prev, cur, cur.next];
  }
  return prev;
};

1 Page Cheat Sheet - dohdat/leetcode-practice GitHub Wiki

Sort hashmap by value

Indegree && Outdegree

Shortest Path:

Dijkstra (weighted)

Bellman Ford

All paths from Source to Target:

Topological Sort (Cycle Detection):

Union Find (Disjoint Set):

Intervals:

Fast & slow pointers:

Heap (Priority Queue):

Longest Common Subsequence

Backtracking:

Permutations

Combinations

Sliding Window:

Stack:

Two Pointers:

BFS:

Iterative

DFS:

In-order:

Pre-order:

Post-order:

Find the number of islands in a grid.

Binary Search:

Linked list cycle

Reverse a linked list

⚠️ **GitHub.com Fallback** ⚠️

⚠️ GitHub.com Fallback ⚠️