Análisis de algoritmos - doapps/software GitHub Wiki

1. ¿Qué es un algoritmo?
2. Eficiencia algorítmica
3. Notación 'Big Oh'
4. Ejemplos
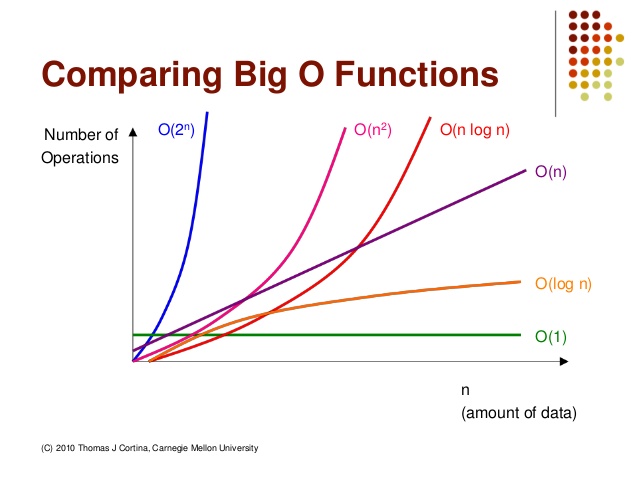
5. Comparación de eficiencias
6. Conclusiones

• Es un conjunto ordenado de instrucciones bien definidas, inámbiguas y finitas que permite resolver un determinado problema computacional.
• Corolario: Un problema computacional puede ser resuelto por diversos (infinitos) algoritmos.

Ejercicio: Select sort (Ordenamiento por selección)

Diseñar buenos algoritmos (soluciones) para resolver determinados problemas.

¿Cómo se mide un algoritmo?

Una manera objetiva de determinar que tan "bueno" es un algoritmo es por medio del número de operaciones básicas que este debe realizar para resolver un problema cuyo tamaño tiene una entrada (n).

¿Qué es una operación básica?

Es cualquier operación que tenga que hacer el computador.

Ejemplo: Una asignación, una suma, una lectura, etc.

• Considerar el peor escenario
• Realizar un análisis asintótico (enfocarse en valores grandes de n).
• No prestar atención a términos constantes o de orden menor.

Ejemplo: Bubble sort (Ordenamiento por burbuja)

Ejemplo 1

for(int i=0; i<n; i++){
}

Las operaciones básicas son:

• 1 -> asignación

• n+1 -> comparaciones

• n -> incrementos

  1 + n + 1 + n = 2n + 2

  Complejidad: 2n+2

  Orden: O(n)

Ejemplo 2

int c = 0;
for(int i=0; i<n; i++){
  for(int k=0; k<n; k++){
  c++;
  } 
}

Las operaciones básicas son:

• 1 -> asignación

• 2n+2 -> 1er. for

• n(2n+2) -> 2do. for

• 1nn -> incremento

  1 + 2n + 2 + n(2n + 2) + 1 * n * n = 3n^2 + 4n + 3

  Complejidad: 3n^2 + 4n + 3

  Orden: O(n^2)

Ejemplo 3

int 1 = 1;
while(i<n){
  i= i * 2;
}

Las operaciones básicas son:

• 1 -> asignación

• log2(n)+1 -> comparaciones

• log2(n) -> multiplicaciones

  1 + log2(n)+1 + log2(n) = 2 + 2log2(n)

  Complejidad: 2 + 2log2(n)

  Orden: O(log(n))

Ejercicio:

[ACM 138] (https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=74)

• Un determinado problema computacional puede ser resuelto por infinitos algoritmos, pero por lo general no siempre dichas soluciones son las más eficientes.
• El análisis de algoritmos busca medir cuán eficiente es una solución en términos de cantidad de operaciones básicas que realiza el computador (a mayor cantidad de operaciones básicas el algoritmo es más malo, y a menor cantidad es más bueno).
• La notación "Big Oh" nos permite estandarizar la forma de definir orden de complejidad de un algoritmo en base al tamaño del problema.
• Una buena forma de practicar es revisar código escrito por nosotros mismos y preguntarse si se puede hacer mejor.

• Notación Big O
• Análisis de complejidad
• Select sort
• Ejemplos