12. Estimating Genome Sizes using k mer Counts - davidaray/Genomes-and-Genome-Evolution GitHub Wiki
Bacterial assemblies are all well and good but many of us are interested in the genomes of eukaryotes. Even the smallest genomes of eukaryotes are substantially larger and more complex than most bacterial genomes. But before we get to the actual assembly, you need to get some data and I want to demonstrate how we can estimate genome size from k-mer calculations.
ESTIMATING THE GENOME SIZE
Here’s an interesting exercise. One way to evaluate the assembly is to first estimate how big it should be before actually doing any assembling. It’s possible to do that using the raw data via the k-mer distribution. Once you get your assembly, you can then compare to your initial estimate and see how well your assembler did.
The theory is: For a given sequence of length L, and a k-mer size of k, the total k-mer’s possible (K) will be given by K = (L – k)+1. Given any two values, one can solve for the last. L = K + k - 1.
For example, assume a sequence of length (L) = 15. For k = 14, the total number of k-mers (K) is 2.
ATGTCTAAGGCGGGT
k-mer1 = ATGTCTAAGGCGGG
k-mer2 = TGTCTAAGGCGGGT
For L = 15 and k = 10, there are 6 k-mers (K).
k-mer1 = ATGTCTAAGG
k-mer2 = TGTCTAAGGC
k-mer3 = GTCTAAGGCG
k-mer4 = TCTAAGGCGG
k-mer5 = CTAAGGCGGG
k-mer6 = TAAGGCGGGT
If we assume a sequence of length (L) = 100. For k = 18, the total number of k-mers (K) is 83. You can write them all out if you want. See the table below for various L and K values for a k-mer of 18.
| K | K + k - 1 | Estimated genome size (L) |
|---|---|---|
| 83 | 83 + 18 - 1 | 100 |
| 983 | 983 + 18 - 1 | 1000 |
| 9983 | 9983 + 18 - 1 | 10000 |
| 99983 | 99983 + 18 - 1 | 100000 |
| 999983 | 999983 + 18 - 1 | 1000000 |
So, by counting the number of k-mers in the raw data (and taking into account rates of sequencing errors and levels of coverage, which adds some uncertainty), we are able to estimate the size of the genome being assembled. A caveat for this process, though. The size of k-mers should be large enough allowing the k-mer to map uniquely to the genome (a concept used in designing primer/oligo length for PCR). Too large k-mers leads to overuse of computational resources.
So how does this actually work?
GETTING A GENOME SIZE ESTIMATE
In the first step, k-mer frequency is calculated to determine the coverage of the genome achieved during sequencing. There are software tools like Jellyfish that help in finding the k-mer frequency. The k-mer frequency follows a pseudo-normal (Poisson) distribution around the mean coverage in a histogram of k-mer counts. Once k-mer frequencies are calculated, a histogram is plotted to visualize the distribution and to calculate mean coverage.
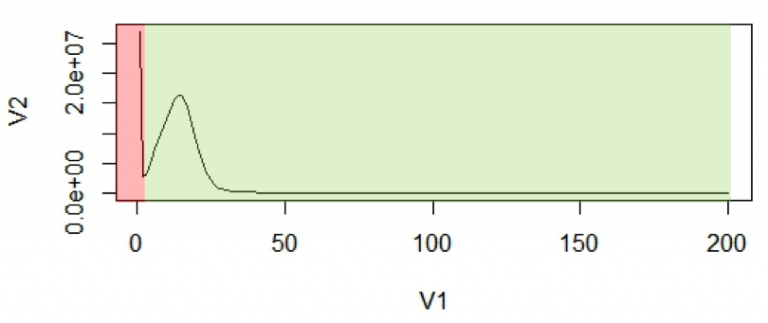
The first peak (in red region) is primarily due to rare and random sequencing errors in reads. These are singletons and rare k-mers (note the low frequency values on the X-axis). If a genome has been sequenced to reasonable coverage, this is what would be expected if they were due to mistakes rather than actual representation in the genome. The values in this region of the graph can be trimmed, thereby removing reads with sequencing errors.
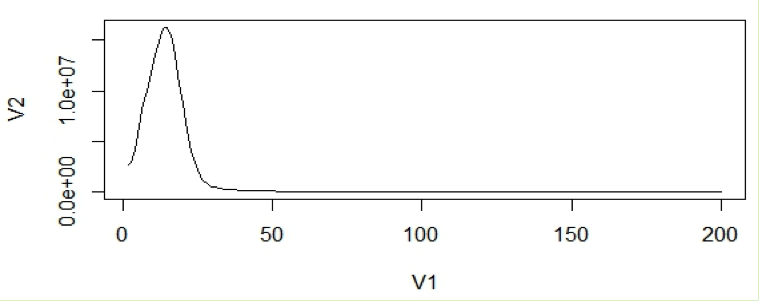
With the assumption that k-mers are uniquely mapped to genome, they should be present only once in a genome sequence. So, their frequency will reflect the coverage of the genome.
- Is this a safe assumption for any eukaryotic genome? Why or why not? Reply in Assignment 11 - K-mer counting.
For calculation purposes we use mean coverage (C) which is 14 in the above graph. The area under the curve will represent the total number of k-mers.
So the genome size estimation (N) will be:
N = area under the curve/mean coverage, or
N = K/C
We’ll do this using the following commands and confirming that it works by estimating the size of the H. pylori genome.
ESTIMATE THE SIZE OF THE H. PYLORI GENOME
Now do this:
mkdir /lustre/scratch/[eraider]/gge2024/jellyfish_work
cd /lustre/scratch/[eraider]/gge2024/jellyfish_work
WORKDIR=/lustre/scratch/[eraider]/gge2024
GGE_CONTAINER=/lustre/scratch/[eraider]/gge2024/container
zcat ../data/helicobacterpylori/short_reads_1.fastq.gz | singularity exec -B $WORKDIR:$WORKDIR $GGE_CONTAINER/gge_container_v4.sif jellyfish count -C -m 21 -s 1000000000 -t 10 -o hpshortreads1.jf /dev/fd/0
A short explanation
- zcat unzips the data without creating a new file, feeding it directly into the next program in your pipe.
- the usual stuff to access the Singularity container version of jellyfish
- -C tells jellyfish to count reads from both strands of DNA
- -m indicates the k-mer size
- -s is the hash size ( ¯\_(ツ)_/¯ ask a computer scientist, has something to do with memory allocation)
- -t use X processors/threads
- -o denote the output file
- /dev/fd/0 is a way of telling bash to take the output of the first command in your pipe as the input for the second command in your pipe.
Now, create a text file with histogram data.
singularity exec -B $WORKDIR:$WORKDIR $GGE_CONTAINER/gge_container_v4.sif jellyfish histo hpshortreads1.jf >hpshortreads1.histo
Take a look at it.
less hpshortreads1.histo
Here are the first 14 lines:
| Frequency | # k-mers |
|---|---|
| 1 | 4109905 |
| 2 | 115082 |
| 3 | 14611 |
| 4 | 6050 |
| 5 | 3499 |
| 6 | 2321 |
| 7 | 2046 |
| 8 | 1627 |
| 9 | 1227 |
| 10 | 954 |
| 11 | 788 |
| 12 | 595 |
| 13 | 414 |
| 14 | 427 |
How do you read this table? Row 1 tells us that there are 4109905 k-mers that occur only once. In other words, there are 4109905 unique k-mers. Row 2 indicates that there are 115082 k-mers that occur twice. And so on. Remember, these low frequency k-mers typically contain sequencing errors and aren't actually represented in the genome. So, they can't help us with this process much but they can still be used for assembly algorithms that take such errors into account. That was shown when you viewed your assembly in Tablet in the last exercise.
We'll first do a VERY rough manual calculation of the genome size using some estimates from the data. Download your .histo file to your local computer and open it in Excel. Highlight the second column and create a bar graph using the 'Insert' tab. Using Assuming you're working on a real computer (read "Windows machine"), you can right click on the Y-axis values and format the values to logarithmic. The resulting plot should look like the one in the figure below. There are two peaks, one at 1 on the X-axis and a second near 90. The trough between them reaches it's lowest point around 30. That that tells us that the error-ridden reads are the in the 1-30-ish bins and the less error-prone reads are to the right of that. While there are undoubtedly some reads in those bins that are not error-prone, we will ignore everything to the left of ~30.

To calculate the genome size, N = K/C (N = area under the curve/mean coverage), we can multiply the number of times a given k-mer occurs by the number of k-mers in that bin and then sum those values from ~30 to the end of the histogram. If we then divide that number by the coverage, represented approximately by the peak of the curve (90-ish), we should get a reasonable estimate of the genome size. For this example, open the file linked here.
From that file (cell F31) you can see that I got an estimate of ~1.75 million bases.
- How does that compare to the genome size of our best assembly (hp_long_high)? Upload your response and your spreadsheet with the calculations to the appropriate assignment on Blackboard.
But, that value is just a rough estimate. Use a web browser to open http://genomescope.org/. Genomescope will use a more formalized set of equations to estimate your genome size. Upload your .histo file to this site and fill in the appropriate fields to see the results. Note that you will need to remember what k-mer size we decided to test when you started this exercise and how long the reads were. You can use the default for 'max k-mer coverage'. If you're interested in really getting to know how Genomescope works, here is a page on the topic.

NOTE: The Genomescope website sometimes goes down during various times in some semesters. Please use the instructions below instead of the ones above if that's the case this semester.
Genomescope has a command line version as well. If you're having problems with the website, please proceed as follows.
Assuming you still have a 10 processor interactive session, in your jellyfish_work directory, run the following command, filling in the necessary options:
module --ignore-cache load gcc/10.1.0 r/4.0.2
SCOPE=/lustre/work/daray/software/genomescope/
Rscript $SCOPE/genomescope.R hpshortreads1.histo 21 100 .
This should run the genomescope.R script that I installed for this exercise in my own software directory. Note that the command is run as follows:
Rscript tells HPCC that you are using an R package. Next comes the jellyfish histogram that you generated, hpshortreads1.histo. That's followed by the kmer size we want to use, 21, and the length of the reads that were used, 100. This should generate the same plots that you would have gotten from running the same thing on the website. You're mostly interested in the plot.png file.
NOTE: End of note.
Note the estimated coverage and the estimated genome size in the text at the top of the figure and the table below the figure (haploid length). Pretty close to what we got before, huh?
So, why does this work? Let's use a much simpler example to illustrate. The phi-X174 viral genome is simple and small. It is not repetitive and only 5386 bp long. If you count the 27-mers in that genome and how many times they appear, you will get data that look like this.
| Frequency | # k-mers |
|---|---|
| 1 | 5360 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 0 |
| 6 | 0 |
| 7 | 0 |
| ... and so on, zeros all the way down. |
In other words, every 27-mer in that genome occurs only once. You can just add up the 27-mer frequency (1 x 5360) and get a pretty good idea of the genome size. 5360 is pretty close to 5386.
Now, imagine if we doubled the size of that genome by duplicating the entire thing and sticking the two pieces together. The resulting genome would be 10,772 bp long but each 27-mer would now be present twice.
| Frequency | # k-mers |
|---|---|
| 1 | 0 |
| 2 | 5360 |
| 3 | 0 |
| 4 | 0 |
| 5 | 0 |
| 6 | 0 |
| 7 | 0 |
| ... and so on, zeros all the way down. |
It still works. 2 x 5360 = 10,720, a good estimate of the duplicated genome size. Just as we did for the more complicated H. pylori genome, all we're doing is finding the peak of the curve and adding the k-mer frequencies (the area under the curve) to determine the likely genome size.
GETTING SOME EUKARYOTIC DATA
We’ll be using data from this publication https://genome.cshlp.org/content/28/2/266.long. In the paper, the authors used a combination of Illumina short read data and Nanopore long read data to generate a highly contiguous Caenorhabditis elegans genome assembly. I’ve downloaded the data but you need get a copy.
interactive -p nocona
cd /lustre/scratch/[eraider]/gge2024
cp -r /lustre/scratch/daray/gge2024/data/celegans data/celegans
Above, I noted that more data is required for eukaryotic genomes. The C. elegans genome is relatively small for a eukaryote, only about 100 Mb but that’s still two orders of magnitude larger than the bacterial genomes previously assembled by you. Even simple eukaryotic genomes like this one are much more complex than the genomes of any bacterium. They therefore require not a proportional amount of data but much higher sequencing depth to resolve the large numbers of repeats that characterize them. To illustrate this to yourself type the following:
ls -lhrt /lustre/scratch/[eraider]/gge2024/data/celegans
ls -lhrt /lustre/scratch/[eraider]/gge2024/data/helicobacterpylori
You’ll notice that the short read data from the files for C. elegans (they start with "N2" and "H9") range from 1.1 to 3.4 Gb. That’s a substantial increase from the largest short read file from H. pylori, 187 Mb.
FOR YOU TO DO
Now, take one of the smaller sets of paired end Illumina reads from the C. elegans data directory (for example, H9_S5_L001_R1_001.fastq.gz) and determine what the likely genome size and coverage is using genomescope. DO NOT just use the same commands as above please. Demonstrate that you understand what was done by changing the filenames as appropriate for this new genome. Use a k-mer size of 27, please. Be aware that you will also need to determine the read lengths for the C. elegans data. Hint: judicious use of zcat and head would be helpful. You might also use fastqc. Finally, keep in mind what I wrote earlier about using more than one processor for this part of the exercise. This is a LOT of data. The more processors you use, the more RAM you will have access to. If you get a .err file that says 'killed', you ran out of memory.
- Upload a screenshot of your results to Blackboard under Assignment 12 - K-mer counting.