The vision behind our project is to create a user-friendly, interactive web app that educates on and makes correct conversions of Euler Angles to quaternions. The goal is to provide information to users who want to better understand Euler angles and the use of quaternions in 3D rotation, as well as information about the conversion methods, specifically when the conversion of a quaternion to Euler angles is unable to return the expected values.

Euler angles are three angles that describe the rotation of an object concerning a fixed coordinate system. Because the three angles can be applied in different orders, resulting in different rotations, Euler angles are represented by twelve rotation sequences. While Euler Angles are incredibly useful for understanding the orientation of an object, there are limitations to using them based on a phenomenon known as Gimbal Lock, which is where quaternions become very useful. The quaternion number system is a 4D extension of the complex number system, consisting of a scalar and a vector component. Though difficult to fully understand how it works, the quaternion number system has become a great tool when describing orientation in 3d space. Therefore it is useful for Euler Angles to be converted to quaternions using one of twelve methods based on the rotation sequence of the angles.

Unfortunately, there are some issues with the conversion methods from quaternions to Euler angles in addition to a lack of information on the internet regarding all twelve of the conversion methods. Since the methods use trigonometric functions, specifically arcsin, arctan, and arccos, there is a limited range of values that can be returned from these methods, meaning that when Euler angles are converted into a quaternion, it may not be possible to get these same angles back out from the conversion of quaternion to Euler angles. Therefore, this web application will seek not only to make the correct conversions for users but also to provide information regarding the range of values that each method is able to return and show how the methods work at a deeper level.

Some other goals for this project include giving information concerning the mathematics behind Euler angles, rotation matrices, and quaternions, providing an interactive graph showing various rotations of an object and the corresponding quaternions, and recommending additional resources to users for more information.

• Computer

• Code: Python, JavaScript, LaTeX, HTML, CSS
• Microframeworks: Flask (Python Web Framework), JupyterHub, Bootstrap
• Server Provider: AWS
• Team Communication: Discord, GroupMe
• Code Editor: Visual Studio Code

This is a list of our user stories and their corresponding acceptance criteria, with many divided between what we consider to be a novice or an expert user. We gave a rating for the estimated effort for each task on a scale from 1 to 10, with 10 taking the most effort. A novice user has just entered the world of 3D rotation and is looking for a deeper understanding, while an expert user is well versed in conversions, possibly in a corporate setting.

• As a general user, I want to be able to input an Euler angle and see the output of the corresponding quaternion, and vice versa.
  • Given I need to perform a transformation and I input the appropriate values, I will receive the proper and accurate result.
  • Estimated time: 30 hours
  • Estimated effort: 10
• As a novice user, I want to receive an explanation of the various rotations of the Euler angles to gain understanding.
  • Given I do not understand a type of rotation, I will be able to click a button and receive an explanation.
  • Estimated time: 3 hours
  • Estimated effort: 3
• As a novice user, I want the output to update as the various inputs change so I can see incremental differences.
  • Given I want to change the coordinate or rotation of an angle, and I input a new value, I will receive a new result instantly.
  • Estimated time: 5 hours
  • Estimated effort: 4
• As a novice user, I want to see a graph that is aligned with my input to fully visualize the conversion.
  • Given that I want to convert a set of Euler angles to a quaternion and that I input correct values, an image on a graph representing the converted angle will be available for me to view.
  • Estimated time: 20 hours
  • Estimated effort: 8
• As a novice user, I want to know when conversion back to Euler may produce a different result than expected so I will not be confused.
  • Given I input an Euler angle whose domain causes an issue with the trigonometric functions, I will receive a warning indicating that the resulting Quaternion will possibly correspond to a different set of Euler angles upon conversion.
  • Estimated time: 10 hours
  • Estimated effort: 6
• As a novice user, I want guidance so I do not get stuck on issues in interpretation.
  • Given I am confused, and I click on a link to help documentation, I will be directed to a page that describes the processes in an easy-to-understand way.
  • Estimated time: 5 hours
  • Estimated effort: 3
• As an expert user, I want a clean, modern interface for conversions that is not bloated with unnecessary, extra information.
  • Given I want to convert an Euler or quaternion angle and visit this web application, I will be able to make these conversions quickly on a user-friendly, clean interface.
  • Estimated time: 20 hours
  • Estimated effort: 8
• As a novice user, I want to be able to interact with a graph and move it around to better understand the values I input.
  • Given I want to interact with a graph, I will be able to input my values and then move the graph around using my cursor.
  • Estimated time: 30 hours
  • Estimated effort: 10
• As a general user, I want to learn more about quaternions and 3D rotations easily without spending hours researching them.
  • Given I want to learn more about quaternions and 3D rotations easily, I will be able to click a button that directs me to a learning center with little write-ups about these topics.
  • Estimated time: 12 hours
  • Estimated effort: 6
• As a novice user, I want to access additional resources about quaternions and 3D rotations without having to search for them on the internet.
  • Given I want to access additional resources, I will be able to click a button that directs me to a page where all additional resources are displayed, and a search bar allows me to narrow them down.
  • Estimated time: 8 hours
  • Estimated effort: 5
• As a novice user, I would like to learn more about linear algebra and the concepts that make these conversions possible at a more fundamental level so that when I read about 3D rotation, I can better understand it.
  • Given, I would like to learn more about linear algebra and the fundamental concepts behind these conversions, I will be able to easily access lessons that dive into linear algebra topics.
  • Estimated time: 15 hours
  • Estimated effort: 7
• As a general user, I would like to know how Convert+ can be used in a practical way and why the converter is important with its various types of conversions.
  • Given, I would like to know how Convert+ can be used in a practical way and why the converter is important, I will be able to read about its uses and practicality in specific industries and fields of study on the home page.
  • Estimated time: 3 hours
  • Estimated effort: 3
• As a general user, I would like to access a calculator to perform matrix operations and the operations talked about in the lessons.
  • Given, I would like to access a calculator to perform additional operations linked to the lessons, I will be able to find a link in the lessons to a related calculator or access it through a calculator landing page.
  • Estimated time: 25 hours
  • Estimated effort: 9

• Complete the quaternion to Euler angle converter implementation
  • Create a rotation model that displays the conversions
• Scale website to fit different screens
• Additional converters
  • Determinant calculator, inverse operator, transpose operator
    • Map new matrix operation calculators to the lessons for greater interaction
  • Derivative calculator
  • Triangle solver
• New test cases
  • Individual test cases
  • Integration test cases
• Fix broken links

• As a novice user, I want to see a graph that is aligned with my input to fully visualize the conversion.
  • Configure form boxes and create a user friendly rotation model for quaternion to Euler angles converter
  • Priority: 9 , Sprint Effort Estimation: 4
• As a general user, I would like to access a calculator to perform matrix operations and the operations talked about in the lessons.
  • Add in additional converters for linear algebra concepts
  • Priority: 7 , Sprint Effort Estimation: 7
• As a novice user, I want to access additional resources about quaternions and 3D rotations without having to search for them on the internet.
  • Fix the links to the additional resources and make sure that the titles match the content of the link.
  • Priority: 6 , Sprint Effort Estimation: 1
• As a general user, I want to be able to input an Euler angle and see the output of the corresponding quaternion, and vice versa.
  • Finish implementation of quaternion to Euler angles converter
  • Priority: 9 , Sprint Effort Estimation: 7
• As a novice user, I would like to learn more about linear algebra and the concepts that make these conversions possible at a more fundamental level so that when I read about 3D rotation, I can better understand it.
  • Make the lessons more interactive by implementing the matrix operation calculators within them.
  • Priority: 8 , Sprint Effort Estimation: 3

General Assignments and Priorities: The focus for this sprint has been on the addition of new converters and calculators as well as the completion of the quaternion to Euler angles converter. We had a lot of new ideas coming into Sprint 6 about ways to expand our website and reach a wider range of users through the implementation of matrix operation calculators, a derivative calculator, and a triangle solver. The matrix operation calculators can make the lessons more interactive for the users since they will be able to access them as they read about the specific operations.

We were able to complete the implementation of a determinant calculator and plan to add in one for multiplication, the inverse, and the transpose. The triangle solver was also implemented successfully as well as the derivative calculator. Beyond the addition of these calculators, we worked to fix up a few flaws we saw in our website specifically with some broken links.

Individual Tasks:

Keely: During this sprint, I focused on the backend side of the determinant calculator. I spent some time researching and learning more about HTML and javascript, specifically how to change HTML dynamically. For the backend of the determinant function, I had to make sure I was collecting the values correctly from the pop-up window and creating the matrix accurately from these values using math.js. Once we finished the calculator, I attached it to the bottom of the determinant lesson so that users can have it accessible upon learning about it.

Issa: In this sprint, I started working by searching for what converters we can add to the site. I was excited about adding a derivative calculator with our nice interface and mobile capability as there aren't many options that offer to calculate a derivative. On the front end I started by creating a page with Latex input to show the mathematical syntax then later replaced it with Katex for better support. when working on the backend I found out that Maxima the service developed by MIT and uses Lisp language to do the calculation does not have an API and we must install the software on a machine but there is no documentation on how to integrate the machine and the JS code. Aside from that, AWS started notifying us about reaching 85% of our free computing so I paused. Next, I created a Triangle Values calculator that accepts the Coordinates of Vertices and outputs the measurements of the sides, angles, area, and perimeter. To do that I coded mathematical formulas using JavaScript and tested the calculator to check the output values, that it does not accept wrong input types, and it has initial values.

Yao: In this sprint, my primary task was to refine the front-end code, such as fixing the issue with the "Contact Us" page where users couldn't input information and linking all the pages together. I also spent some time searching for new features to add to the website. I added a trigonometric function converter, where users can input an angle and see its corresponding trigonometric functions in a Cartesian coordinate system. With the help of some open-source websites, I wrote JavaScript code to visualize trigonometric functions. When users first enter this page, they can see an animation of a Cartesian coordinate system. Then, when they input an angle, they can see its various sides displayed in different colors in the image in real-time. However, the UI of this page still needs some refinement.

Adam: I was focused on the front-end development of the determinant calculator this sprint. I did research on writing JavaScript code to insert HTML items into a page dynamically based on user input. I developed and tested this grid for calculating the determinant and implementing it in a modal. I also spent some time making various incremental edits to the UI in some of the converter pages to match the overall theme. Lastly, I communicated with Keely to help with the integration of the front and back ends.

Sammy: My main focus through this sprint was finishing and debugging the Triangle Solver first implemented in sprint 5. I rearranged the code to ensure that the reset button would provide the triangle dimensions to return to 0, but the triangle image generated is not disappearing properly, causing duplications. I also have looked into other options for rendering the triangle since Three.js has convoluted and complex methods for adding text to images and for deleting meshes from canvases. I have yet to find a viable option but will continue to investigate in the next sprint.

Keely:

Test 1:

• Purpose: To test the accuracy of the determinant calculator based on input values for the matrix that should return the determinant value of zero.
• Setup: Navigate to the determinant calculator from the Converters Home page. Input the value 3 into the text box to give the matrix 3 rows and columns.
• Inputs:

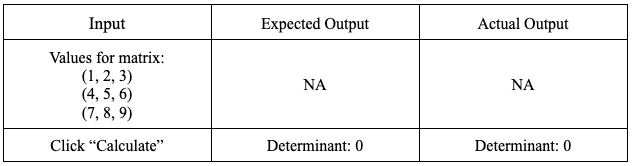
Test 2:

• Purpose: To test the accuracy of the determinant calculator based on input values for the matrix that should return a determinant value less than zero.
• Setup: Navigate to the determinant calculator from the Converters Home page. Input the value 3 into the text box to give the matrix 3 rows and columns.
• Inputs:

Test 3:

• Purpose: To test the accuracy of the determinant calculator based on input values for the matrix that should return a determinant value greater than zero.
• Setup: Navigate to the determinant calculator from the Converters Home page. Input the value 3 into the text box to give the matrix 3 rows and columns.
• Inputs:

Coverage:

• Tests for determinant calculator accuracy:
  • Matrix size 2: Test inputs for determinants equal to, greater than, and less than zero
  • Matrix size between 3 and 9 inclusive: Test inputs for determinant equal to, greater than, and less than zero
  • Matrix size 10: Test inputs for determinant equal to, greater than, and less than zero
• Coverage of Tests 1-3: 3/9 = 33.3%

Adam:

My tests were focused on navigating various instances of the determinant calculator.

Test 1:

Purpose - Test the "Make Matrix" button on the determinant calculator.

Setup - Navigate to the determinant calculator.

Inputs - This test was concerned with the generation of the matrix grid based on user input. I am testing to see if it works as intended for several inputs. I am also testing the functionality of the close buttons' ability to reset the matrix upon click.

Input	Expected Output	Actual Output
Type "2" in the input box	The number appears in the box	The number appears
Click the "Make Matrix" button	The modal appears on screen with the correct matrix grid generated	The correct matrix appears
Type numbers into each box	The numbers are accepted as input	The numbers are accepted
Click "Close", and click "Make Matrix" again	The same modal pops up with an empty 2x2 matrix	The modal appears with an empty matrix
Close the modal, type "11" into the input box, click "Make Matrix"	The modal pops up with the message "Please Enter A Valid Size."	The error message appears in the modal
Close the modal, type "2.2" into the input box, click "Make Matrix"	The modal pops up with the message "Please Enter A Valid Size."	The modal appears with a 3x3 grid

Coverage - 5/6 = 83.3%

Test 2:

Purpose - Testing the matrix modal after performing calculations.

Setup - Navigate to the determinant calculator and open the modal with a generated 2x2 matrix.

Inputs - This test was concerned with testing the determinant calculation modal to see if it can repeatedly perform calculations without overloading the UI. I am also checking if reopening the modal still allows calculation without page refresh.

Input	Expected Output	Actual Output
Type "2", "3", "4", and "5" in order to the generated 2x2 matrix, and click "Calculate"	The determinant appears with the answer of -2	The correct value appears
Press "Calculate" 4 more times	The determinant value stays without duplicating the result	The result stays the same
Change "4" in the matrix to "10" and press calculate	The determinant value updates to -20	The value updates as indicated
Reopen the modal with the 2x2 matrix	The previous determinant result no longer appears	The previous result no longer appears
Type "1", "2", "7", and "8" in order again and click "Calculate"	The determinant value appears with a new value of -6	The value -6 appears

Coverage - 5/5 = 100%

Test 3:

Purpose - Test the separate determinant calculator on the determinant lesson.

Setup - Navigate to the "Trace, Determinant, Inverse" lesson.

Inputs - This test was focused on the implementation of the determinant calculator that is embedded in the determinant lesson. It checks for UI glitches that could occur since the code was ported directly from the standalone determinant calculator page.

Input	Expected Output	Actual Output
Type "2" in the input box and press "Make Matrix"	The modal pops up with a 2x2 matrix grid and no graphical errors	The modal appears as expected
Close the modal	The "Trace, Determinant, Inverse" lesson is still readable with no graphical errors	The lesson is readable
Click the "Make Matrix" button when it is slightly below and off-screen	The modal appears in the same place as before, centered and entirely visible	The modal appears in the correct place

Coverage - 3/3 = 100%

Sammy:

Test 1:

Purpose – Test the different Triangle Methods for 3-4-5 Triangle

Setup – Navigate to Triangle Solver

Inputs – The user inputs either SSS, SAS, AAS, or ASA depending on the test case with the specific 3-4-5 Triangle dimensions.

Input	Expected Output	Actual Output
Select “SSS” and click “Select”. Type in 3 for Side 1, 4 for Side 2, and 5 for Side 3 into boxes and click “Solve”	Side1: 3, Side2=4, Side3=5 Angle1=36.87, Angle2=53.13, Angle3=90, Triangle Image generated	Side1: 3, Side2=4, Side3=5 Angle1=36.87, Angle2=53.13, Angle3=90, Triangle Image generated
Select “SAS” and click “Select”. Type in 3 for Side 1, 90 for angle 3 and 4 for Side 2 and click “Solve”	Side1: 3, Side2=4, Side3=5 Angle1=36.87, Angle2=53.13, Angle3=90, Triangle Image generated	Side1: 3, Side2=4, Side3=5 Angle1=36.87, Angle2=53.13, Angle3=90, Triangle Image generated
Select “ASA” and click “Select”. Type in 53.13 for Angle 2, 3 for Side 1 and 90 for Angle 3 and click “Solve”	Side1: 3, Side2=4, Side3=5 Angle1=36.87, Angle2=53.13, Angle3=90, Triangle Image generated	Side1: 3, Side2=4, Side3=5 Angle1=36.87, Angle2=53.13, Angle3=90, Triangle Image generated
Select “ASA” and click “Select”. Type in 36.87 for Angle 1, 53.13 for Angle 2 and 3 for Side 1 and click “Solve”	Side1: 3, Side2=4, Side3=5 Angle1=36.87, Angle2=53.13, Angle3=90, Triangle Image generated	Side1: 3, Side2=4, Side3=5 Angle1=36.87, Angle2=53.13, Angle3=90, Triangle Image generated
Coverage: 4/4 = 100%

Test 2:

Purpose – Test the resetting of values within the Triangle Solver

Setup – Navigate to Triangle Solver

Inputs – The user inputs either SSS, SAS, AAS, or ASA with the specific 3-4-5 Triangle dimensions. These tests deal with checking resetting values either with the reset button or recalculating.

Input	Expected Output	Actual Output
Select “SSS” and click “Select”. Type in 3 for Side 1, 4 for Side 2, and 5 for Side 3 into boxes and click “Solve” Click “Solve” one more time with the same inputs.	All values should stay the same for the triangle and the triangle image should not duplicate.	Sides and angles stayed the same. Triangle image was duplicated under the previous image.
Click “Reset”	All values should reset to 0 and triangle images should disappear	All values are reset to 0 but triangle images remain.
Coverage: 0/2 = 0% (Caused by triangle image)

Test 3:

Purpose – Navigating from Triangle Solver to other parts of the website.

Setup – Navigate to Triangle Solver

Inputs – Click the Menu bar on the top right corner and select the following options.

Input	Expected Output	Actual Output
Click “Converters” Click “Euler to Quaternion”	Euler to Quaternion converter page is loaded.	Euler to Quaternion converter page loaded.
Click “Lessons” Click Lesson 5:”Special Trig Identities”	“Special Trig Identities” lesson page is loaded.	“Special Trig Identities” lesson page loaded.
Click “Home”	“Home” page is loaded.	“Home” page loaded.
Click “Contact Us”	“Contact Us” page is loaded	“Contact Us” page loaded.
Coverage: 4/4 = 100%

Integration Testing:

• Purpose: To test that the components working behind the determinant calculator are working together properly, specifically that the javascript code is calling the right elements within the html and collecting the right values.
• Setup: Have the determinant calculator display the elements of the matrix that it creates from the input values the user gives rather than the calculated determinant: Change line 28 in Determinant.js to “let num = document.createTextNode(A);”
• Input:

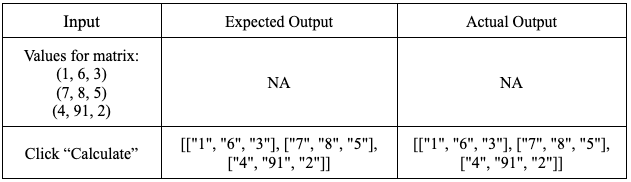
Yao:

Test 1: Input value of Trigonometry Convert

Purpose: Yo test that users can input the value to the block and the coordinate system can display a correct triangle.

Setup: Use the age already built and try to input different values.

Inputs: Try to input the value from 0 to 360, and also test for both negative and positive numbers.

Input	Expected Output	Actual Output
0	shows a line	shows a line
360	shows a line	shows a line
-1	do not accept "-"	same as expectes
34	shows a right triangle	same as expected
560	shows the angle -360 degree if is over 360 degrees	show 200 degrees
Coverage: 5/5 = 100%

Test 2:

Purpose: To test that all the values shown is correct

Setup: Use the age already built and try to input different values.

Inputs: Try to input the value from 0 to 360, and also test for both negative and positive numbers.

Input	Expected Output	Actual Output
0	all zero	all zero
360	only shows degree as 360, other value will be zero	same as expected
-1	do not accept "-"	same as expectes
34	shows a right triangle	same as expected
560	shows the angle -360 degrees if is over 360 degrees	same as expected
75	shows at quadrant 1, radian 0.785	same as expected
Coverage: 6/6 = 100%

Garron:

Test 1: Test Quaternion To Euler Input Boxes

Purpose: Test is to assure only proper input values are allowed in the text boxes.

Setup: Use the website interface to test various values (not including alphanumeric).

Inputs:

Input	Expected Output	Actual Output
a, 0, 0	reject input	reject input
-4, 4, 4	processes a negative value	processes a negative value
A, 0, 0	reject input	reject input
4, 4, 4	processes Euler input	processes Euler input
Coverage: 4/4 = 100%

Test 2:

Purpose: To test positive and negative rotation for the renderer.

Setup: Use the age already built and try to input different values.

Inputs: Input both positive and negative values, and see if the app renders it properly.

Input	Expected Output	Actual Output
-4, 4, 4	rotates counter-clockwise, then clockwise, then clockwise	rotates counter-clockwise, then clockwise, then clockwise
Coverage: 1/1 = 100%

Issa:

Test 1: Test Triangle values by coordinates of vertices, input box

Purpose: The test is to assure only proper input values are allowed in the text boxes.

Setup: Use the website interface to test various values (not including alphanumeric).

Inputs:

Input	Expected Output	Actual Output
[2,-2], [a, 0], [0,0]	reject input	reject input
[2,-2], [0, 0], [5,0]	shows a value	shows a value
[2,-2], [/, 0], [0,0]	reject input	reject input
Coverage: 3/3 = 100%

Test 2: Checking the output for each box

Purpose: Make sure that the calculation is correct

Inputs:

Input	Expected Output	Actual Output
[2,-2], [5, 0], [0,0]	side a = 5	side a = 5
[2,-2], [5, 0], [0,0]	side b = 2.83	side b = 2.83
[2,-2], [5, 0], [0,0]	side c = 3.61	side c = 3.61
[2,-2], [5, 0], [0,0]	Angle α = 101.31	Angle α = 1.768
[2,-2], [5, 0], [0,0]	Angle β = 33.69	Angle β = 0.588
[2,-2], [5, 0], [0,0]	Angle γ = 45.00	Angle γ = 0.785
[2,-2], [5, 0], [0,0]	Perimeter = 11.44	Perimeter = 11.44
[2,-2], [5, 0], [0,0]	Area = 5	Area = 5

Coverage: 5/8 = 62.5%

For this test, I found out that the output is by radians and not in degrees so I added a conversion.

Input	Expected Output	Actual Output
[2,-2], [5, 0], [0,0]	side a = 5	side a = 5
[2,-2], [5, 0], [0,0]	side b = 2.83	side b = 2.83
[2,-2], [5, 0], [0,0]	side c = 3.61	side c = 3.61
[2,-2], [5, 0], [0,0]	Angle α = 101.31	Angle α = 101.31
[2,-2], [5, 0], [0,0]	Angle β = 33.69	Angle β = 33.69
[2,-2], [5, 0], [0,0]	Angle γ = 45.00	Angle γ = 45.00
[2,-2], [5, 0], [0,0]	Perimeter = 11.44	Perimeter = 11.44
[2,-2], [5, 0], [0,0]	Area = 5	Area = 5

Coverage: 8/8 = 100%