Product Vision:

The vision behind our project is to create a user-friendly, interactive web app that educates on and makes correct conversions of Euler Angles to quaternions. The goal is to provide information to users who want to better understand Euler angles and the use of quaternions in 3D rotation, as well as information about the conversion methods, specifically when the conversion of a quaternion to Euler angles is unable to return the expected values.

Euler angles are three angles that describe the rotation of an object with respect to a fixed coordinate system. Because the three angles can be applied in different orders, resulting in different rotations, Euler angles are represented by twelve rotation sequences. While Euler Angles are incredibly useful for understanding the orientation of an object, there are limitations to using them based on a phenomenon known as Gimbal Lock, which is where quaternions become very useful. The quaternion number system is a 4D extension of the complex number system, consisting of a scalar and a vector component. Though difficult to fully understand how it works, the quaternion number system has become a great tool when describing orientation in 3d space. Therefore it is useful for Euler Angles to be converted to quaternions using one of twelve methods based on the rotation sequence of the angles.

Unfortunately, there are some issues with the conversion methods from quaternions to Euler angles in addition to a lack of information on the internet regarding all twelve of the conversion methods. Since the methods use trigonometric functions, specifically arcsin, arctan, and arccos, there is a limited range of values that can be returned from these methods, meaning that when Euler angles are converted into a quaternion, it may not be possible to get these same angles back out from the conversion of quaternion to Euler angles. Therefore, this web application will seek not only to make the correct conversions for users but also to provide information regarding the range of values that each method is able to return and show how the methods work at a deeper level.

Some other goals for this project include giving information concerning the mathematics behind Euler angles, rotation matrices, and quaternions, providing an interactive graph showing various rotations of an object and the corresponding quaternions, and recommending additional resources to users for more information.

Hardware:

• Computer

Software:

• Code: Python, Mathematica
• Microframeworks: Flask (Python Web Framework), JupyterHub
• Server Provider: AWS
• Team Communication: Discord, GroupMe
• Code Editor: Visual Studio Code

Product Backlog:

This is a list of our user stories and their corresponding acceptance criteria, with many divided between what we consider to be novice or an expert users. We gave a rating for the estimated effort for each task on a scale from 1 to 10, with 10 taking the most effort. A novice user has just entered the world of Euler to quaternion angles and is looking for a deeper understanding, while an expert user is well versed in conversions, possibly in a corporate setting.

• As a general user, I want to be able to input an Euler angle and see the output of the corresponding quaternion, and vice versa.
  • Given I need to perform a transformation and I input the appropriate values, I will receive the proper and accurate result.
  • Estimated time: 30 hours
  • Estimated effort: 10
• As a novice user, I want to receive an explanation of the various rotations of the Euler angles to gain understanding.
  • Given I do not understand a type of rotation, I will be able to click a button and receive an explanation.
  • Estimated time: 3 hours
  • Estimated effort: 3
• As a novice user, I want the output to update as the various inputs change so I can see incremental differences.
  • Given I want to change the coordinate or rotation of an angle, and I input a new value, I will receive a new result instantly.
  • Estimated time: 5 hours
  • Estimated effort: 4
• As a novice user, I want to see a diagram to fully visualize the conversion.
  • Given that I want to convert an angle from Euler to quaternion and input correct values, an image representing the converted angle will be available for me to view.
  • Estimated time: 10 hours
  • Estimated effort: 7
• As a novice user, I want to know when conversion back to Euler may produce a different result so I will not be confused.
  • Given I input an Euler angle whose domain causes an issue with the trigonometric functions, I will receive a warning indicating that the resulting quaternion angle will possibly correspond to a different Euler angle upon conversion.
  • Estimated time: 10 hours
  • Estimated effort: 7
• As a novice user, I want guidance so I do not get stuck on issues in interpretation.
  • Given I am confused, and I click on a link to help documentation, I will be directed to a page that describes the processes in an easy-to-understand way.
  • Estimated time: 5 hours
  • Estimated effort: 3
• As an expert user, I want a clean interface for conversions that is not bloated with unnecessary, extra information.
  • Given I want to convert an Euler or quaternion angle and visit this web application, I will be able to quickly and smoothly make these conversions.
  • Estimated time: 3 hours
  • Estimated effort: 1
• As a novice user, I want to be able to interact with a graph and move it around to better understand the values I have input.
  • Given I want to interact with a graph, I will be able to input my values and then move the graph around using my cursor.
  • Estimated time: 10 hours
  • Estimated effort: 7
• As a general user, I want to learn more about quaternions and 3D rotations easily without spending hours researching them.
  • Given I want to learn more about quaternions and 3D rotations easily, I will be able to click a button that directs me to a learning center with little write-ups about these topics.
  • Estimated time: 12 hours
  • Estimated effort: 6
• As a novice user, I want to access additional resources about quaternions and 3D rotations without having to search for them on the internet.
  • Given I want to access additional resources, I will be able to click a button that directs me to a page where all additional resources are displayed, and a search bar allows me to narrow them down.
  • Estimated time: 8 hours
  • Estimated effort: 5

Sprint 1 Goals:

• Create an outline for our website and decide what pages it will have

• Research and pull together the 12 mathematical methods for the conversion of Euler angles to a quaternion, and a quaternion to Euler angles.

• Look at how different languages implement trig functions and find the best language for implementing the twelve methods. Then begin implementing these methods.

• Find libraries for Euler angle and quaternion conversions that are available for different languages.

• Investigate the ways in which the rotations can be displayed to the user(Mathematica, MatPlot, etc)

• Debug and review Keely's previously implemented methods for errors or flaws, and begin finding the ranges of values that can be returned from the quaternion to Euler methods.

• Organize GitHub and add information on the Wiki specifically regarding the Sprint 1 Review.

• Work on the Architecture Diagram

Sprint 1 Backlog:

• As a general user, I want to be able to input an Euler angle and see the output of the corresponding quaternion, and vice versa.

• As a novice user, I want to know when conversion back to Euler may produce a different result so I will not be confused.

General Assignments and Priorities:

This sprint was mostly focused around learning about and researching quaternions and 3D rotation. Since our web application will be centered around the complex mathematics of making conversions from quaternions to Euler angles and vice versa, and because there is little information provided on these topics, our goal was to look deeper into the mathematics for ourselves and figure out the implementations of the conversion methods in python. While we all took part in researching and learning, the python implementations were mostly the job of Garron and Sammy. Our group will continue to work on the implementation and research of these conversion methods throughout the semester. The two user stories above are two of the biggest priorities for this project, which is why our focus for this sprint was aimed at solving their problems.

A big part of this sprint was also organizing and figuring out the layout for this project as well as deciding what the goals of this project ultimately will be. Keely worked on wording the product vision and goals, while Adam worked on the user stories and product backlog. Issa and Yao helped with researching the best way to go about implementing our web application and the software that would be used for this project. The hope is that this sprint will have better set us up to get our web app working efficiently in future sprints.

Individual Tasks:

Keely: During this sprint, I spent the majority of my time familiarizing myself with the different types of web apps and researching/implementing the best type of design architecture for our web app. I worked on creating the design architecture diagram and crafting the product vision and goals, as well as adding to our wiki. On the math side of things, I spent time looking for resources that could help our team learn more about quaternions and reached out to my manager from my summer internship to pull resources from the work I did this summer.

Adam: My job during this sprint was researching the aspects of Euler to quaternion conversion in order to gain a proper understanding as we set forth through development, as this was a new concept to me, and it is very important to fully comprehend what kinds of math that we are working with before diving in. I created the user stories to immerse ourselves into the perspectives of our future users, dividing the requirements between what we defined as a novice or expert users. I also read over Keely's previous code with Euler and quaternion conversions to get a general idea of how exactly they worked.

Sammy: My first task in this sprint was familiarizing myself with Euler angles and Quaternions. Next was understanding how to convert between the two and researching the issues that can occur between their conversion (Gimbal lock). The rest of my job during this sprint was working with Garron on discovering different libraries that could be used within Python to make these conversions and to see if any of them circumvent the issues at hand.

Garron: My job during this sprint was to familiarize myself with the mathematics behind Euler angles and quaternions and how we can perform these calculations on a website using Python. I also read over Keely's previous code to give myself a starting point on how the conversions are normally implemented. In addition to this, I also explored a couple different options for an interactive notebook in the website (Jupyter Notebook or Mathematica and which one would be better) that can enhance the user's learning experience. I also explored the possible use of rotation matrices during the conversion to serve as an intermediary for the data.

Yao Wang: In this sprint, I first spent time studying Euler angles (which was a new concept for me). Then I ran and analyzed the sample code provided by Keely using the Jupyter notebook, which helped me understand the basic concepts of our project. Since our project will eventually be presented as a website, I have researched several possible options to host our website (e.g. GitHub Pages). But our final choice has not been decided yet. After that, I reviewed the websites I had made to help me quickly recall CSS, HTML, Javascript, and Python. I also worked on viable visualization APIs that can be used in web development (e.g. Manim, Matplotlib, and Plotly).

Issa: During this sprint, I spent time familiarizing myself with the mathematics behind Euler angles and quaternions, and convertor projects. I looked up helpful python libraries online like [three.js] and how numeric computing platforms apply some of the methods and convert them to C. I looked up developing web frameworks to compile the code online like [django and Flask] and reached out to TU's IT to get potential web space. I also looked up other hosting options like AWS and Github. Finally, I looked for front-end development frameworks like Bootstrap.

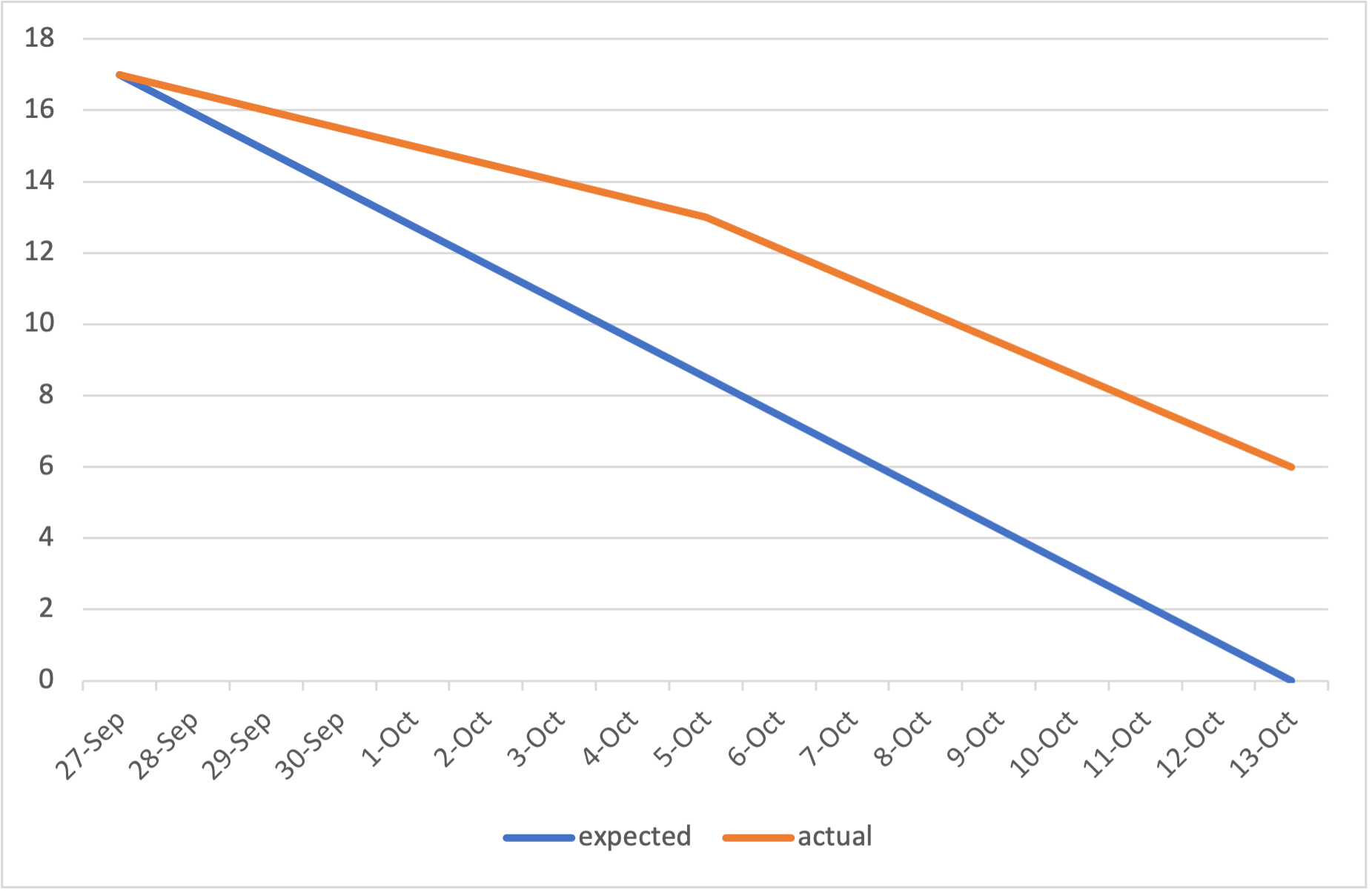
Burndown Chart