Rotate Image - codepath/compsci_guides GitHub Wiki

Problem Highlights

• 🔗 Leetcode Link: Rotate Image
• 💡 Problem Difficulty: Medium
• ⏰ Time to complete: 25 mins
• 🛠️ Topics: Array, 2D-Array
• 🗒️ Similar Questions: Transpose Matrix, Flipping an Image

1: U-nderstand

Understand what the interviewer is asking for by using test cases and questions about the problem.

• Established a set (2-3) of test cases to verify their own solution later.
• Established a set (1-2) of edge cases to verify their solution handles complexities.
• Have fully understood the problem and have no clarifying questions.
• Have you verified any Time/Space Constraints for this problem?

• Can the input grid be blank??
  • Let’s assume the grid is not blank. We don’t need to consider empty inputs.
• Can the row size be different from the column size?
  • No, the row size is equal to the column.
• What are the time and space constraints?
  • Time complexity should be O(m*n), m being the rows of the matrix and n being the columns of matrix. Space complexity should be O(1).

HAPPY CASE
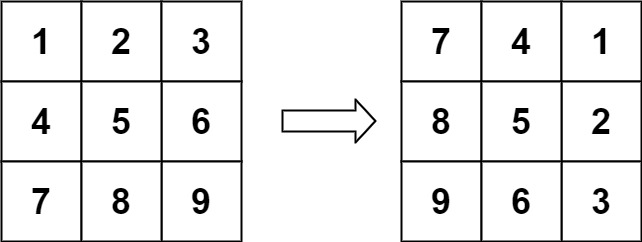
Input: matrix = [1,2,3],[4,5,6],[7,8,9](/codepath/compsci_guides/wiki/1,2,3],[4,5,6],[7,8,9)
Output: [7,4,1],[8,5,2],[9,6,3](/codepath/compsci_guides/wiki/7,4,1],[8,5,2],[9,6,3)

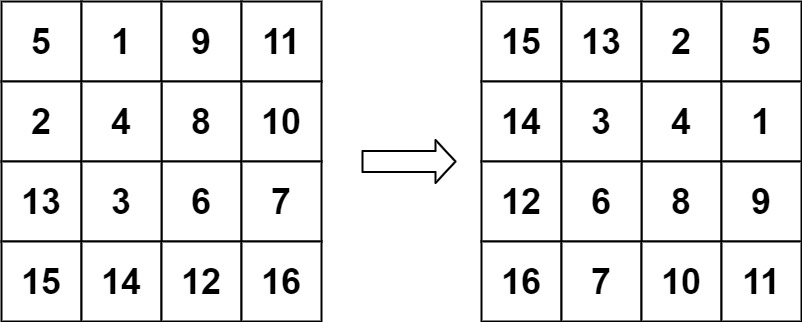
Input: matrix = [5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16](/codepath/compsci_guides/wiki/5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16)
Output: [15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11](/codepath/compsci_guides/wiki/15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11)

EDGE CASE
Input: matrix = [1](/codepath/compsci_guides/wiki/1)
Output: [1](/codepath/compsci_guides/wiki/1)

2: M-atch

Match what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.

For 2D-Array, common solution patterns include:

• Perform a BFS/DFS Search through the 2D Array
  • A search through the 2D Array (either BFS or DFS) does not help us. We are rotating an image.
• Hash the 2D Array in some way to help with the Strings
  • Hashing would not help us flipping a image horizontally, then inverting it
• Create/Utilize a Trie
  • A Trie would not help us much in this problem since we are not trying to determine anything about a sequence of characters.

3: P-lan

Plan the solution with appropriate visualizations and pseudocode.

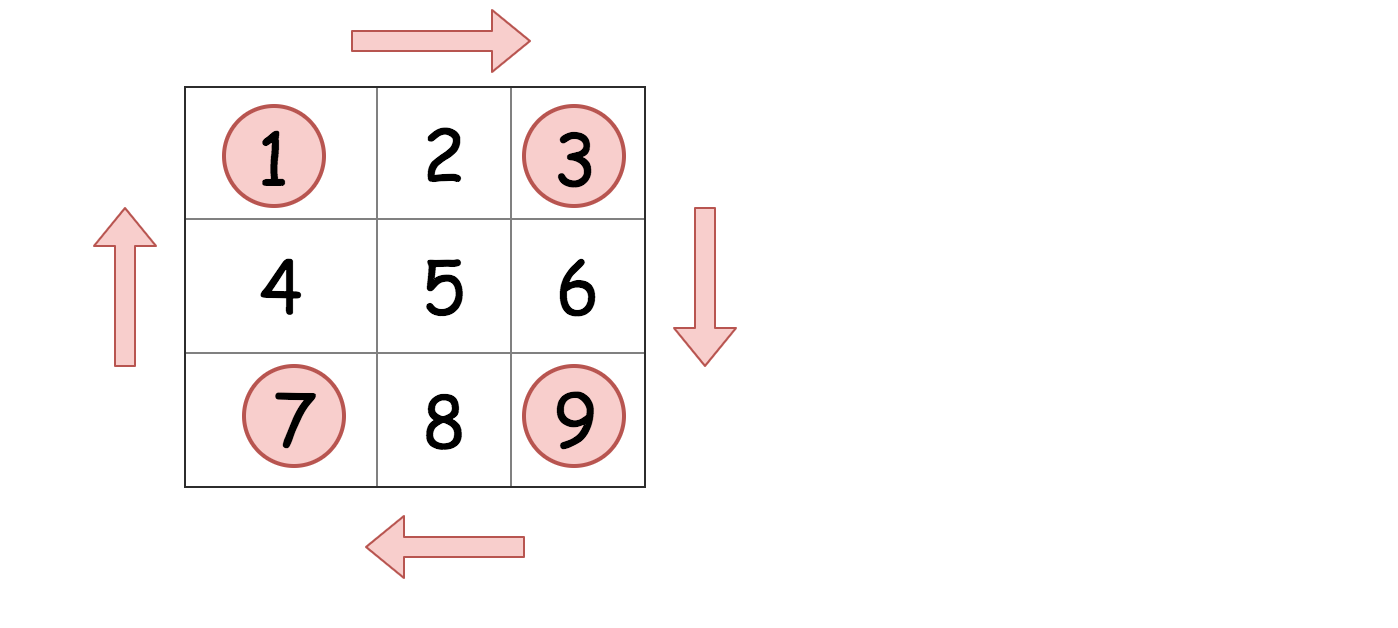
General Idea: Let's recursively rotate each item layer by layer.

1) Create a helper function with the boundary for rotation
    a)Basecase: Single square
    b)Rotate the items from upper-row with left-column, left-column with bottom-row, bottom-row with right-column, and right-column with upper-row
        i) Store upper-row
        ii) Set upper-row with value in left-column
        iii) Set left-column with value in bottom-row
        iv) Set bottom-row with value in right-column
        v) Set the right-column with upper-row
    c)Recursive reduce the layers
2) Run helper function starting at the outermost layer

⚠️ Common Mistakes

• Not every 2D-Array problem follows the common techniques.

4: I-mplement

Implement the code to solve the algorithm.

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        "
        Do not return anything, modify matrix in-place instead.
        "
        def helper(top_left, bottom_right):
            # Basecase: Single square 
            if bottom_right <= top_left:
                return

            # Rotate the items from upper-row with left-column, left-column with bottom-row, bottom-row with right-column, and right-column with upper-row
            for i in range(top_left, bottom_right):
                tmp = matrix[top_left][i] # Store upper-row
                matrix[top_left][i] = matrix[n-i][top_left] # Set upper-row with value in left-column
                matrix[n-i][top_left] = matrix[n-top_left][n-i] # Set left-column with value in bottom-row
                matrix[n-top_left][n-i] = matrix[n-(n-i)][n-top_left] # Set bottom-row with value in right-column
                matrix[n-(n-i)][n-top_left] = tmp # Set the right-column with upper-row

            # Recursive reduce the layers
            helper(top_left+1, bottom_right-1)
        
        # Run helper function starting at the outermost layer
        n = len(matrix)-1
        helper(0, n)

class Solution {
    public void rotate(int[][] matrix) {
        // Run helper function starting at the outermost layer
        int n = matrix.length;
        solve(matrix, n, 0);
        return;
    }
    
    void solve(int[][] matrix, int n, int start){
        // Basecase: Center square 
        if(start >= n/2){
            return;
        }
        
        // Rotate the items from upper-row with left-column, left-column with bottom-row, bottom-row with right-column, and right-column with upper-row
        for(int i = start; i < n-1-start; i++){
            int a = matrix[start][i];
            int b = matrix[i][n-1-start];
            int c = matrix[n-1-start][n-i-1];
            int d = matrix[n-i-1][start];
            
            matrix[start][i] = d;
            matrix[i][n-1-start] = a;
            matrix[n-1-start][n-i-1] = b;
            matrix[n-i-1][start] = c;
        }
        
        // Recursive reduce the layers
        solve(matrix, n, start+1);
    }
}

5: R-eview

Review the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.

• Trace through your code with an input to check for the expected output
• Catch possible edge cases and off-by-one errors

6: E-valuate

Evaluate the performance of your algorithm and state any strong/weak or future potential work.

Assume N represents the number of rows in 2D-array. Assume M represents the number of columns in 2D-array.

• Time Complexity: O(N * M) we need to rotate each item in the 2D-Array
• Space Complexity: O(1), because we are not using any additional space, we rotate the image in-place.