0986. Interval List Intersections - chasel2361/leetcode GitHub Wiki

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.
The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval.
For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

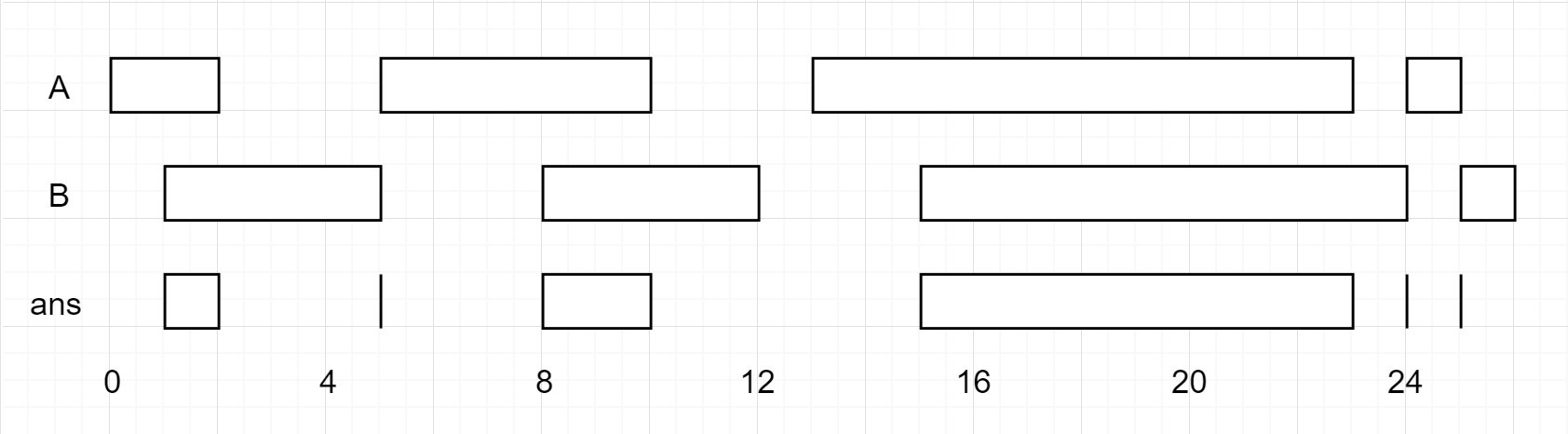
Example 1:
Input:
A = [ [0,2],[5,10],[13,23],[24,25] ],
B = [ [1,5],[8,12],[15,24],[25,26] ]
Output: [ [1,2],[5,5],[8,10],[15,23],[24,24],[25,25] ]
Reminder: The inputs and the desired output are lists of Interval objects, and not arrays or lists.

Note:
0 <= A.length < 1000
0 <= B.length < 1000
0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9
NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.

這一題要求在兩個陣列組間尋找交點，有條理的方法是將陣列組逐一取出，取下限的大值與上限的小值，若下限 <= 上限表示有相交，最後比較上限，上限較小的陣列組往前推進。

[1] 若指標 A, B 其中之一超出範圍就不用找了，絕對不會相交
[2] 下限大值 < 上限小值表示有相交
[3] 上限較小者將指標往前走

class Solution:
    def intervalIntersection(self, A, B):
        intersection = []
        i, j = 0, 0        
        while i < len(A) and j < len(B):  #[1]
            low = max(A[i][0], B[j][0])
            high = min(A[i][1], B[j][1])
        
            if low <= high:  #[2]
                intersection.append([low, high])        
            if A[i][1] < B[j][1]:  #[3]
                i += 1
            else:
                j += 1        
        return intersection

這樣寫的時間複雜度為 O(M+N)，空間複雜度為 O(M+N)