0098. Validate Binary Search Tree - chasel2361/leetcode GitHub Wiki

Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
● The left subtree of a node contains only nodes with keys less than the node's key.
● The right subtree of a node contains only nodes with keys greater than the node's key.
● Both the left and right subtrees must also be binary search trees.

Example 1:
Input: [2,1,3]
Output: true

Example 2:
Input: [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

這題的概念是二元搜尋樹，是二元樹的進階版，他多了題目所述的三個條件：

1. 任一節點左子樹的所有節點值必小於該節點值
2. 任一節點右子樹的所有節點值必大於該節點值
3. 二元搜尋樹的左右子樹亦為二元搜尋樹

圖形大概會長這樣

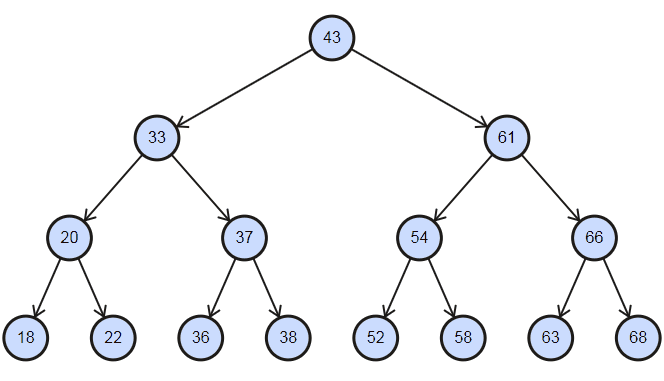
簡單來說，在任一節點上只要往左走會變小、往右走會變大，如此儲存資料的方式可以達到 Binary Search 的效果。

因此在二元搜尋樹中，若要將資料從小至大排列必須使用中序 (In-Order) 的遍歷方式，In-Order的順序是左 → 中 → 右，要一路走到最左邊再開始慢慢往右走，實際的遍歷方式會像下圖一樣

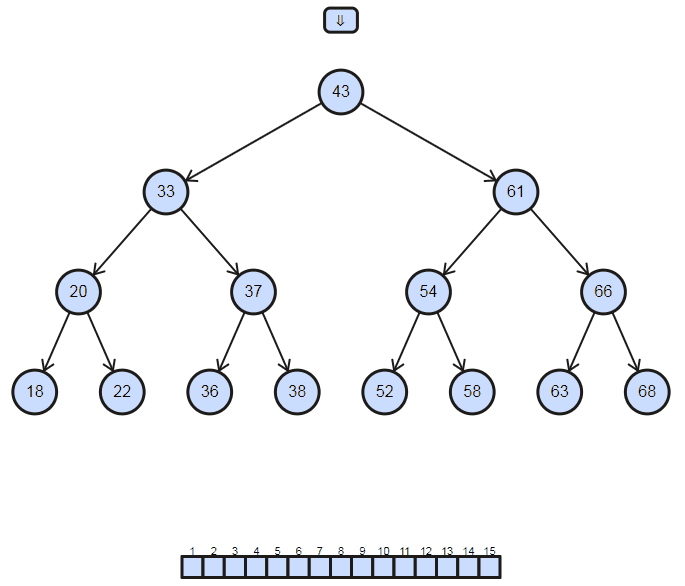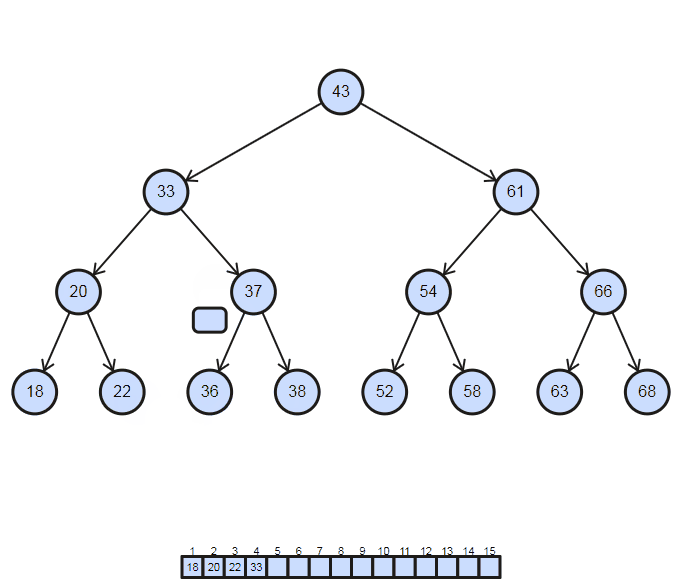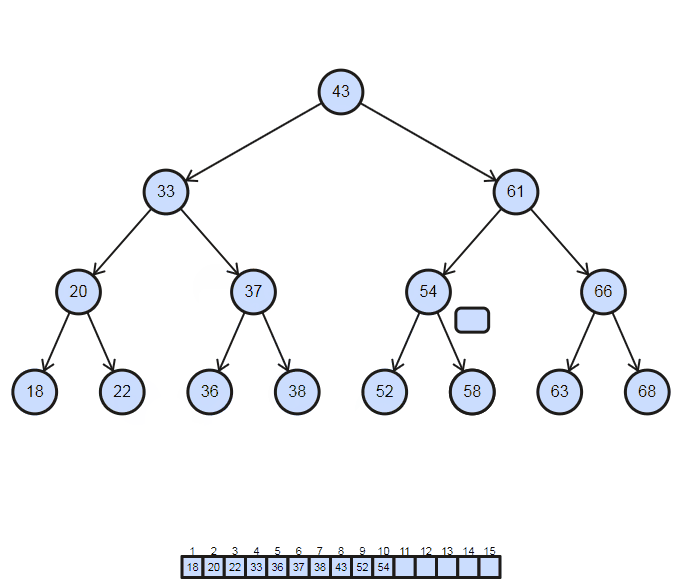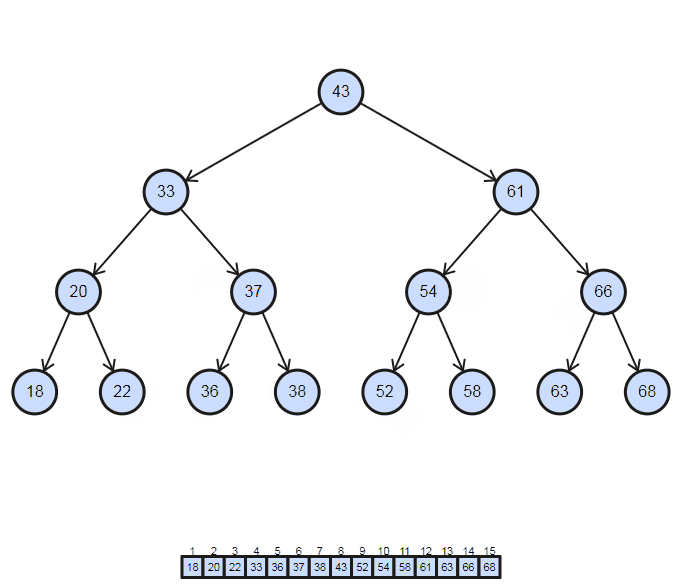
按照這樣把每個值印出來的程式碼可以寫成這樣：

[1] 如果根不存在，那也沒什麼好印的，直接回頭
[2] 如果根存在，先往左子樹走
[3] 如果左子樹不存在，就印出根的值
[4] 往右子樹走，右子樹再開始從左子樹檢查，直到右子樹的右子樹不存在，才印出右子樹根的值

def InOrder(root):
    if not root: return  # [1]
    InOrder(root.left)  # [2]
    print(root.val)  # [3]
    InOrder(root.right)  # [4]

所以如果要判斷一棵樹是否為二元搜尋樹的話，就需要記住上一個節點的值，按著 In-Order的順序走時只要遇到當前節點值 ≤ 上一節點值就代表這不是二元搜尋樹，若走到最後都沒有出現問題，就代表這棵樹確實為二元搜尋樹。

[1] 確認根存在後先往左子樹走，如果左子樹的根不存在就往下一行去
[2] 判斷根的值是否大於暫存值，若是就往下走，否的話回傳 False
[3] 如果左子樹的根存在且小於等於暫存值，代表這棵樹不是二元搜尋樹，回傳 False
[4] 將暫存值更新
[5] 往右子樹去，回傳其判定

如此一來就會先往最左邊走，若判定全為 True 的話便會走到最右邊，再回傳 True

class Solution:
    def __init__(self):
        self.last = None
    def isValidBST(self, root: TreeNode) -> bool:
        if not root: return True
        if not self.isValidBST(root.left): return False  # [1], [3]
        if self.last and root.val <= self.last.val: return False  # [2]
        self.last = root  # [4]
        return self.isValidBST(root.right)  # [5]

這樣寫的時間複雜度是 O(N)， 空間複雜度是 O(N) ，但可能會遞迴很多層

---

如果用迭代法來寫的話，會利用 stack 後進先出的特性來儲存走過的節點值，先不停地往左邊走，路過的都丟進 stack 裡，只到最左下角才開始跟暫存值比大小，通過後的話便往右子樹走，繼續往左確認暫存值

[1] 一開始沒有暫存值，先令其為負無限大
[2] 當 stack 以及 root 都不存在時就表示走完整棵樹了
[3] 當最左邊的值不存在時，就往上一階
[4] 往右一格，重複迴圈

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        last = float('-inf')  # [1]
        stack = []
        while stack or root:  # [2]
            while root:
                stack.append(root)
                root = root.left
            root = stack.pop()  # [3]
            
            if root.val <= last:
                return False
            last = root.val
            root = root.right  # [4]
                
        return True

這樣寫的時間複雜度是 O(N), 空間複雜度是O(N)

(最糟的狀況是每個資料都連在左子樹下面，全部都要丟進 stack 裡)