Make a paper airplane with Unity - bosssu/Imagination-and-creativity GitHub Wiki
Today,I opened a brain hole - use Unity's Mesh programming to fold a paper airplane and play.
Without further ado, let's start!
First a simple effect :

After thinking about it, to achieve the effect of a dynamic origami plane, there are several problems that need to be solved.
- Mesh generation.
This is a very common operation and will not be repeated here. But I'm still lazy here and directly use a patch exported from Blender (to achieve a proper effect, make sure that the number of faces is sufficient).

Blender generated mesh
- Polyline mark.
It is well understood that to achieve dynamic origami, we need to manually mark where to fold on the plane. This mark is a straight line, which is obtained by marking two points on the plane with the mouse (the collision body of the plane is set to MeshCollider, and the world coordinates of the intersection of the plane and the ray can be obtained through ray detection).

- Specific folding logic (emphasis).
Orientation to fold. Imagine that when we usually origami, after we determine the fold line, we need to confirm which direction of the fold line to fold (up or down, left or right). Here, for the sake of being lazy, I'll just assume that every time I'm operating on the area to the right of the polyline (world space, the viewing angle is always the same, aligned with world coordinates). In this way, each time we fold, the vertices we operate on are the vertices on the right of the polyline in world coordinates. So we just need to determine whether the vertex of the mesh is on the right side of the polyline.
This is relatively simple, as shown in the figure:
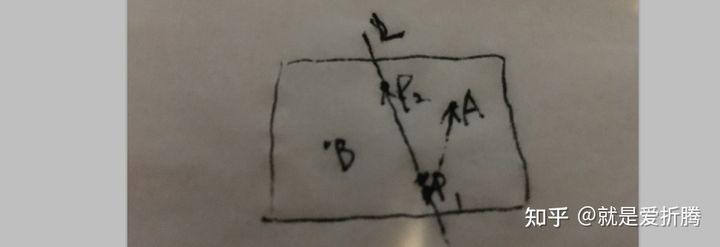
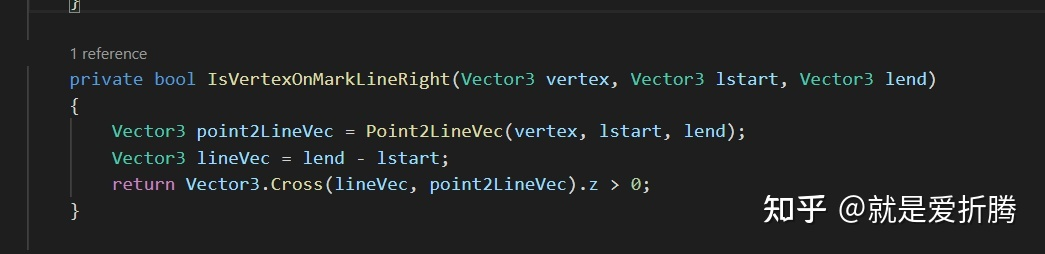
If we like to judge whether point A is on the right side of the polyline L, we only need to cross-multiply P1P2 and P1A to determine whether the z-component of the vector obtained after cross-multiplication is greater than 0 lines (P1P2 is the two points we calibrated. Point A is a vertex of the mesh).
Algorithm for vertex offset.
In fact, the problem to be solved here is one: the vertex rotates around the specified axis (the axis generally does not coincide with the coordinate axis). Here you can use the construction matrix or directly use the rotation method that comes with Unity, which is essentially the same. I won't build a matrix here, I will directly use the rotation method that comes with Unity: Quaternion.AngleAxis(angle,axis)
But the axis of this method requires the origin of the coordinates. And our axis does not necessarily go through the origin, so we need to add two steps to it: first offset the vertex by a vector (the vertical vector from the origin to the polyline), rotate it, and then offset it back. (It is equivalent to moving the polyline to the position past the origin first, and then moving it back after the rotation operation is completed. The method of constructing the matrix is also the same idea).
Finally, the link of this project : https://github.com/bosssu/Imagination-and-creativity/tree/main/Assets/Samples/paperAirPlane