6. 정렬 - bloodfinger8/AlgorithmStudy GitHub Wiki
정렬
퀵정렬
일반적으로 사용되고 있는 아주 빠른 정렬 알고리즘, 분할 정복 알고리즘 중 하나.
방식
- pivot, start, end 를 사용
- 시작점(index:0), 끝점(index:n-1), pivot(index:n/2) 을 정한다.
- arr[start] >= arr[pivot] 에 성립하는 요소를 찾을 때 까지 오른쪽으로 스캔
- arr[pivot] <= arr[end] 에 성립하는 요소를 찾을 때 까지 왼쪽으로 스캔
장단점
- 장점
- 속도가 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다.
- 단점
- 정렬된 리스트는 퀵정렬의 불균형 분할에 의해 n^2의 시간복잡도를 갖음.
구현 코드
public class QuickSort {
static int partition(int[] array,int start, int end) {
int pivot = array[(start+end)/2];
while(start<=end) {
while(array[start]<pivot)
start++;
while(array[end]>pivot) end--;
if(start<=end) {
int tmp = array[start];
array[start]=array[end];
array[end]=tmp; start++; end--;
}
}
return start;
}
static int[] quickSort(int[] array,int start, int end) {
int p = partition(array, start, end);
if(start<p-1) quickSort(array,start,p-1);
if(p<end) quickSort(array,p,end);
return array;
}
public static void main(String[] args) {
int[] array = {4,2,3,5,9};
array = quickSort(array,0,array.length-1);
System.out.println(Arrays.toString(array));
}
}
시간 복잡도

병합정렬
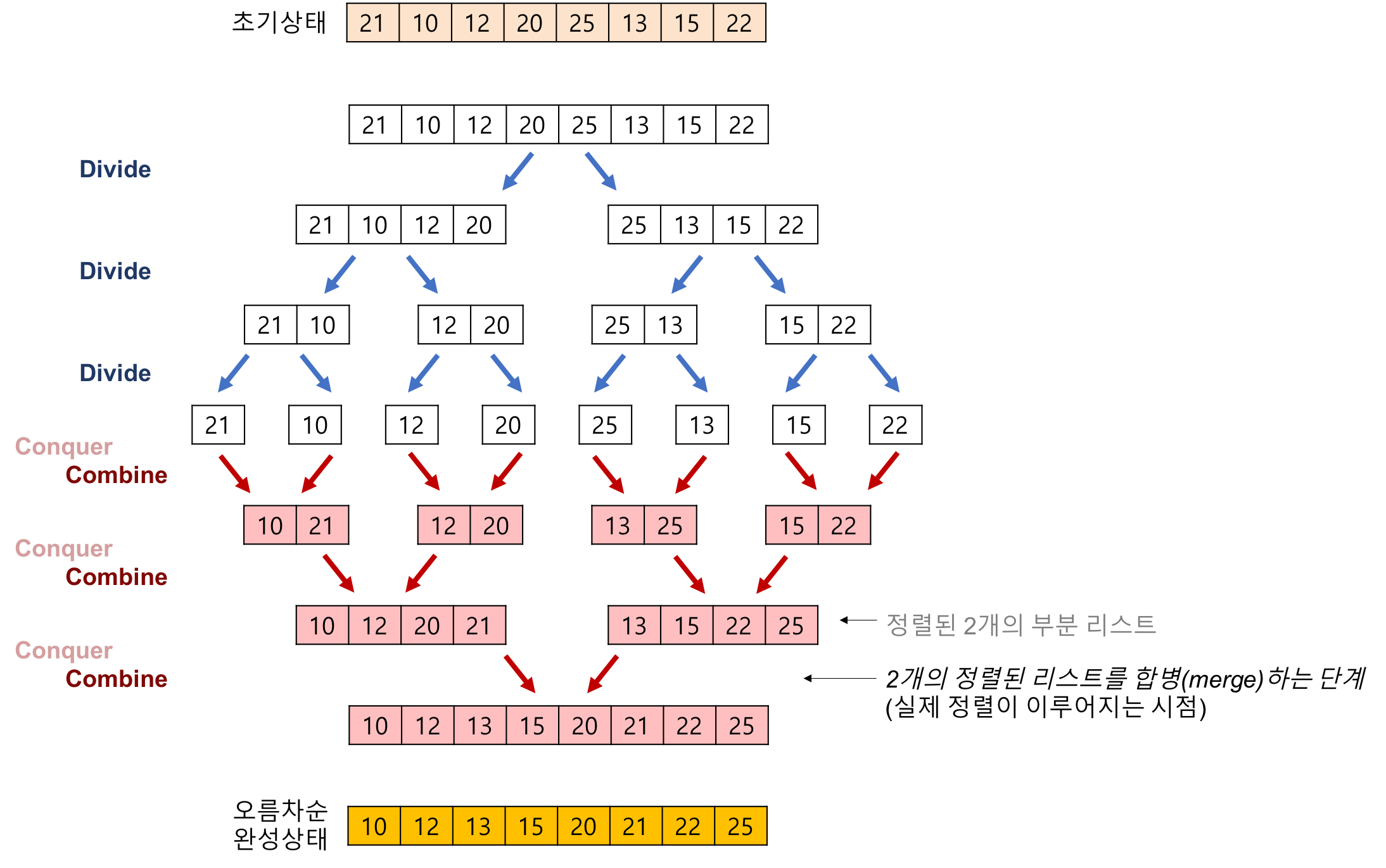
배열을 앞부분과 뒷부분으로 나우어 각각 정렬한 후, 병합하는 작업 반복하여 정렬 수행 (Devide and Conquer)
방식
- Devide : 더 이상 쪼갤 수 없을 때 까지 쪼갠다.
- Conquer : 부분 배열 정렬
- Combine : 정렬된 부분 배열들을 하나의 배열로 합병
구현 코드
public class MergeSort {
static int[] sorted = new int[8];
public static void merge(int a[], int m, int middle, int n) {
int i = m; // 첫 번째 부분집합의 시작 위치 설정
int j = middle+1; // 두 번째 부분집합의 시작 위치 설정
int k = m; // 배열 sorted에 정렬된 원소를 저장할 위치 설정
while(i<=middle && j<=n) {
if(a[i]<=a[j]) {
sorted[k] = a[i];
i++;
}else {
sorted[k] = a[j];
j++;
}
k++;
}
if(i>middle) {
for(int t=j;t<=n;t++,k++) {
sorted[k] = a[t];
}
}else {
for(int t=i;t<=middle;t++,k++) {
sorted[k] = a[t];
}
}
for(int t=m;t<=n;t++) {
a[t] = sorted[t];
}
}
public static void mergeSort(int a[], int m, int n) {
int middle;
if(m<n) {
middle = (m+n)/2;
mergeSort(a, m, middle); // 앞 부분에 대한 분할 작업 수행
mergeSort(a, middle+1, n); // 뒷 부분에 대한 분할 작업 수행
merge(a, m, middle, n); // 부분집합에 대하여 정렬과 병합 작업 수행
}
}
public static void main(String[] args) {
int[] list = {58,8,28,3,18,6,33,20};
mergeSort(list, 0, size-1);
}
}
장단점
- 단점
- 임시의 배열 공간이 필요하다. (퀵소트같은 제자리 배열이 아니다.)
- 레코드 크기가 큰 경우, 이동 시간이 많아 비효율적
- 장점
- 안정적인 정렬 방법 (입력 데이터 관계없이 logN 동일)
- 연결리스트로 구현 시, 링크 인덱스만 변경하여 제자리 정렬로 구현 가능 --> 단점 극복 가능
- 따라서, 큰 레코드의 경우 연결리스트를 이용한 병합정렬은 어느 정렬보다도 효율적.
힙정렬
최댓값이나 최솟값을 찾기위해 고안된 트리 정렬. [참고] 최소 힙 : 루트에 가장 작은 값이 옴 최대 힙 : 루트에 가장 큰 값이 옴
방식
- 최대힙 or 최소힙을 만든다.
- root와 leaf노드를 바꾸고, leaf노드를 제외시킨 후 다시 최대힙 or 최소힙을 만든다.
- 2를 반복한다.
구현 코드
public class HeapSort {
//전체 트리 구조를 최대 힙 구조 만들기
for(int i=1;i<n;i++){
int c = i;
do{
int root = (c-1)/2;
if(heap[root] < heap[c]){
swap(heap[root],heap[c]);
}
c = root
}while(c!=0)
}
// 크기 줄여가면서 반복적으로 힙 구성
for(int i=number-1;i>=0;i--){
swap(heap[i],heap[0]);
int root = 0;
int c = 1;
do{
c = (2 * root) + 1;
if(heap[c]<head[c+1] && c < i - 1){
c++;
}
//root 보다 자식이 더 크면 교환
if(heap[root]<heap[c] && c < i){
swap(heap[root],heap[c]);
}
root = c;
} while(c < i)
}
}
시간복잡도
logN(높이) * N(모든 정점)
도수정렬
도수 정렬은 요소의 대소 관계를 판단하지 않고 빠르게 정렬할 수 있는 알고리즘.
- 단일 for문만을 사용
방식
- 도수분포표 만들기 '각 점수에 해당하는 학생이 몇명인가?' 에 해당하는 배열 만들기
- 누적 도수 분포표 만들기 f[i] += f[i-1] 과정을 반복.
- 목적 배열 만들기 각각의 점수를 받은 학생이 몇 번째에 위치하는지 알 수 있음. 이를 활용하여 정렬함.
- 배열 복사하기
구현 코드
static void fSort(int[] a, int n, int max){
int[] f = new int[max+1];
int[] b = new int[n];
for(int i=0;i<n;i++) f[a[i]]++;
for(int i=1;i<=max;i++) f[i] += f[i-1];
for(int i=n-1;i>=0;i--) b[--f[a[i]]] = a[i];
for(int i=0;i<n;i++) a[i]=b[i];
}