트리

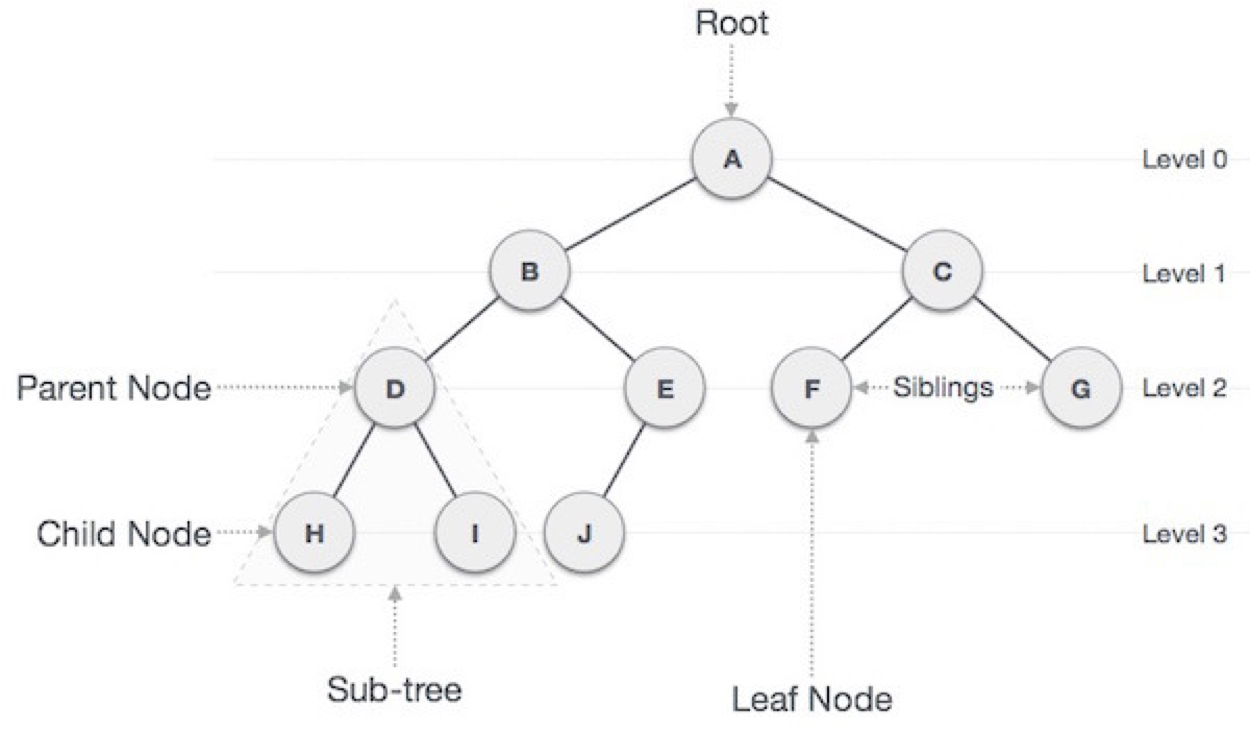
• 루트 노드(root node): 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
• 단말 노드(leaf node): 자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
• 내부(internal) 노드: 단말 노드가 아닌 노드
• 간선(edge): 노드를 연결하는 선 (link, branch 라고도 부름)
• 형제(sibling): 같은 부모를 가지는 노드
• 노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수
• 노드의 깊이(depth): 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
• 노드의 레벨(level): 트리의 특정 깊이를 가지는 노드의 집합
• 노드의 차수(degree): 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
• 트리의 차수(degree of tree): 트리의 최대 차수
• 트리의 높이(height): 루트 노드에서 가장 깊숙히 있는 노드의 깊이

트리(Tree)의 특징

• 그래프의 한 종류이다. ‘최소 연결 트리’ 라고도 불린다.
• 트리는 계층 모델 이다.
• 트리는 DAG(Directed Acyclic Graphs, 방향성이 있는 비순환 그래프)의 한 종류이다.
• loop나 circuit이 없다. 당연히 self-loop도 없다. 즉, 사이클이 없다.
• 노드가 N개인 트리는 항상 N-1개의 간선(edge)을 가진다. 즉, 간선은 항상 (정점의 개수 - 1) 만큼을 가진다.
• 루트에서 어떤 노드로 가는 경로는 유일하다.
• 임의의 두 노드 간의 경로도 유일하다. 즉, 두 개의 정점 사이에 반드시 1개의 경로만을 가진다.
• 한 개의 루트 노드만이 존재하며 모든 자식 노드는 한 개의 부모 노드만을 가진다.
• 부모-자식 관계이므로 흐름은 top-bottom 아니면 bottom-top으로 이루어진다.

출처 : https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html

이진 탐색 트리 (Binary Search Tree)

"탐색을 위한 자료구조로 이진 트리를 사용하기 위해서 저장할 데이터의 크기에 따라 노드의 위치를 정의한 것"

• 전화번호부에서 전화번호를 찾거나

• 서점에서 책을 찾거나

• 지도에서 목적지를 찾는것

등과 같이 자료들 속에서 필요한 자료를 찾아내는 것이 탐색이다.

탐색을 하기 위해서 찾을 자료를 식별할 수 있는 유일한 값이 필요한데 이것을 키(key)라고 한다.

사람을 찾을 때 그 사람을 식별할 수 있는 주민등록번호나 학번을 사용하였다면 이것이 탐색키가 된다.

효율적인 탐색 작업을 위해 이진 탐색 트리를 다음과 같이 정의한다.

(1) 모든 원소는 서로 다른 유일한 키를 갖는다.

(2) 왼쪽 서브 트리에 있는 원소의 키는 그 루트의 키보다 작다.

(3) 오른쪽 서브 트리에 있는 원소의 키는 그 루트의 키보다 크다.

(4) 왼쪽 서브 트리와 오른쪽 서브 트리도 이진탐색 트리다.

\

[ 이진 탐색 트리 탐색 연산 ]

• 탐색은 항상 루트 노드에서 시작한다.

• 먼저, 키값 x와 루트 노드의 키값을 비교한다.

• if (x == 루트) 원하는 원소를 찾았으므로 탐색 성공

• else if (루트 > x) 루트의 왼쪽 서브트리에 대해서 탐색 연산 수행

• else if (루트 < x) 루트의 오른쪽 서브트리에 대해서 탐색 연산 수행

[ 이진 탐색 트리 삽입 연산 ]

• 원소를 삽입하려면 먼저 이진 탐색 트리에 같은 원소가 있는지를 확인하기 위해 탐색을 해야한다.
• if (탐색 성공) 이미 같은 원소가 트리 내에 있는 것이므로 삽입 연산을 수행하지 않는다.
• else if (탐색 실패) 크기를 비교하여 찾아간 노드의 위치에 같은 원소가 없는 것이므로 그 자리에 원소를 삽입

[ 이진 탐색 트리 삭제 연산 ]

• 원소를 삭제하는 경우 자식 노드의 수에 따라 세 가지 경우가 있다.
• 노드를 삭제한 후에도 여전히 이진 탐색트리를 유지해야 하기 때문에 각각의 경우에 따라 후속 처리가 필요하다.

① 삭제할 노드가 단말 노드인 경우

• 노드를 삭제하고, 부모노드의 링크 필드를 null로 설정하는 작업으로 간단히 처리할 수 있다.

출처: https://songeunjung92.tistory.com/31 [은져미]

TreeNode 구현

public class TreeNode {
    char data;
    TreeNode left;
    TreeNode right;
    
    public TreeNode(){
        this.left = null;
        this.right = null;
    }
    
    public TreeNode(char data){
        this.data = data;
        this.left = null;
        this.right = null;
    }
    
    public Object getData(){
        return data;
    }
}

이진탐색 구현

public class BinarySearchTree {
    private TreeNode root = new TreeNode();
    
    public TreeNode insertKey(TreeNode root, char x) {
        TreeNode p = root;
        TreeNode newNode = new TreeNode(x);
        
        if(p==null){
            return newNode;
        }else if(p.data>newNode.data){
            p.left = insertKey(p.left, x);
            return p;
        }else if(p.data<newNode.data){
            p.right = insertKey(p.right, x);
            return p;
        }else{ 
            return p;
        }
    }
    
    public void insertBST(char x){
        root = insertKey(root, x);
    }
    
    public TreeNode searchBST(char x){
        TreeNode p = root;
        while(p!=null){
            if(x<p.data) p = p.left;
            else if(x>p.data) p = p.right;
            else return p;
        }
        return p;
    }
    
    public void inorder(TreeNode root){
        if(root!=null){
            inorder(root.left);
            System.out.print(root.data + " ");
            inorder(root.right);
        }
    }
    
    public void printBST(){
        inorder(root);
        System.out.println();
    }
}