Unit 2 Boolean Arithmetic and the ALU - birdybro/Nand2Tetris_MiSTer GitHub Wiki

Unit 2.1 - Binary Numbers

I know a lot of how this works so only going to take notes on things that are new to me. He brings up negative numbers in binary with half of it. He's vaguely alluding to unsigned versus signed numbers I think... To find what a binary number is in decimal he takes 87 as the example, deoncstructs it by finding the largets number that fits in it from the binary set and going on down, etc... I am asked about 99 so...

99 = 64 + 32 + 2 + 1 which is 1100011. Stuff I knew already, but good to get a refresher and see if any new method was shown.

Unit 2.2 - Binary Addition

How to do addition of binary numbers directly without converting them to decimal? He shows an example of starting the right-most digit and then you have to carry the 1, etc... It's kind of the same thing in binary, but he says it will be easier. 1+1 in binary up and down you don't do 2, you carry the one to the next position, so you keep carrying and adding on up! :P This is stuff I kinda new intuitively because of things like overflow and all that as a concept. Cool!

I'm asked a question here to show I know what it's showing me:

And I got it right. It was a little mind-bending at the carry 1 over 1 and 1, but that's like... you just set it to 1 and carry it on up, which makes sense.

Now he's going to bring up overflow. If the carry that needs to go to the left of the size of the word, it will just ignore it usually. Sometimes in some computers it might actually wrap around push everything to the left but put the carry to the right. If you exceed the word size, then the result you get is not the true number but a truncated one.

Adders

Half Adder - adds two bits
Full Adder - adds three bits
Adder - Adds two numbers

Half adder is taking 2 bits (a, b) and the output is the carry. So looks like you can make a chip that has two inputs (a,b) and two outputs (sum,carry). So I'll make that one now... This is the desired output:

|   a   |   b   |  sum  | carry |
|   0   |   0   |   0   |   0   |
|   0   |   1   |   1   |   0   |
|   1   |   0   |   1   |   0   |
|   1   |   1   |   0   |   1   |

and the code to achieve this is probably like an XOR --> sum and an AND --> carry?

CHIP HalfAdder {
    IN a, b;    // 1-bit inputs
    OUT sum,    // Right bit of a + b 
        carry;  // Left bit of a + b

    PARTS:
    Xor (a=a, b=b, out=sum);
    And (a=a, b=b, out=carry);
}

Success! :) The full adder is next X_X

|   a   |   b   |   c   |  sum  | carry |
|   0   |   0   |   0   |   0   |   0   |
|   0   |   0   |   1   |   1   |   0   |
|   0   |   1   |   0   |   1   |   0   |
|   0   |   1   |   1   |   0   |   1   |
|   1   |   0   |   0   |   1   |   0   |
|   1   |   0   |   1   |   0   |   1   |
|   1   |   1   |   0   |   0   |   1   |
|   1   |   1   |   1   |   1   |   1   |

So this one is a bit confusing but I think I can get it... Essentially the sum is (at the end of things) either an Xor or an XNor operation. The carry is either And or an Or operation. So I need a way to get em to that point but it has 3 inputs which is weird. Actually, not too bad, remember the Mux chip? ;) Just need to use a Mux for column a to select, and then a b in, and i guess the out might be something I'll have to pipe into something else to separate the carry and sum? I'll have to test that out let's see... Since the sum row is either Xor or Xnor (apparently they dont' have a built in Xnor, I forgot I made it out of 5 nand for fun lol), so I'll take the output of the xor of b and c and negate it for an Xnor sum output, and mux that to select the proper sum set of rows in the truth table. Then do the same thing but with And and Or operations into a Mux for the carry.

CHIP FullAdder {
    IN a, b, c;  // 1-bit inputs
    OUT sum,     // Right bit of a + b + c
        carry;   // Left bit of a + b + c

    PARTS:
    Xor  (a=b, b=c, out=XorSum);
    Not  (in=XorSum, out=XnorSum);
    Mux  (a=XorSum, b=XnorSum, sel=a, out=sum);
    And  (a=b, b=c, out=AndCarry);
    Or   (a=b, b=c, out=OrCarry);
    Mux  (a=AndCarry, b=OrCarry, sel=a, out=carry);
}

And it works! :) Next is the 16-bit Adder (ez...?):

|        a         |        b         |       out        |
| 0000000000000000 | 0000000000000000 | 0000000000000000 |
| 0000000000000000 | 1111111111111111 | 1111111111111111 |
| 1111111111111111 | 1111111111111111 | 1111111111111110 |
| 1010101010101010 | 0101010101010101 | 1111111111111111 |
| 0011110011000011 | 0000111111110000 | 0100110010110011 |
| 0001001000110100 | 1001100001110110 | 1010101010101010 |

The truth tables from the comparison file aren't as useful for me immediately with these wider bit chips :P hence why they probably don't test every single possible outcome, it would be too long. This just gives you the idea. Anyways... This might be something like the other 16-bit chips we did earlier, however... I think I need to string the outputs of the full adders into one another, but how? Maybe need to mux the carry select as an on or off? So I think I'll need to at the bare minimum take in the 16 bits, this will be 15 full adders and the 16th will be a half adder since I don't need to worry about the most significant carry bit. So actually it's a half adder first because I need to get the carry started off as the "selector" bit for whether there is a carry or not (a). And... first test of what I just wrote and it works!!

CHIP Add16 {
    IN a[16], b[16];
    OUT out[16];

    PARTS:
    HalfAdder (           a=a[0],  b=b[0],  sum=out[0],  carry=carry0 );
    FullAdder (a=carry0,  b=a[1],  c=b[1],  sum=out[1],  carry=carry1 );
    FullAdder (a=carry1,  b=a[2],  c=b[2],  sum=out[2],  carry=carry2 );
    FullAdder (a=carry2,  b=a[3],  c=b[3],  sum=out[3],  carry=carry3 );
    FullAdder (a=carry3,  b=a[4],  c=b[4],  sum=out[4],  carry=carry4 );
    FullAdder (a=carry4,  b=a[5],  c=b[5],  sum=out[5],  carry=carry5 );
    FullAdder (a=carry5,  b=a[6],  c=b[6],  sum=out[6],  carry=carry6 );
    FullAdder (a=carry6,  b=a[7],  c=b[7],  sum=out[7],  carry=carry7 );
    FullAdder (a=carry7,  b=a[8],  c=b[8],  sum=out[8],  carry=carry8 );
    FullAdder (a=carry8,  b=a[9],  c=b[9],  sum=out[9],  carry=carry9 );
    FullAdder (a=carry9,  b=a[10], c=b[10], sum=out[10], carry=carry10);
    FullAdder (a=carry10, b=a[11], c=b[11], sum=out[11], carry=carry11);
    FullAdder (a=carry11, b=a[12], c=b[12], sum=out[12], carry=carry12);
    FullAdder (a=carry12, b=a[13], c=b[13], sum=out[13], carry=carry13);
    FullAdder (a=carry13, b=a[14], c=b[14], sum=out[14], carry=carry14);
    FullAdder (a=carry14, b=a[15], c=b[15], sum=out[15], carry=carry15);
}

First try and it works! Awesome!

Unit 2.3 - Negative numbers

He goes over two different ways to do negative numbers in binary, either through signed bits (something I know already, could use a mux to use the MSB as the selector bit and swap between using negative or positive) or through 2's complement (which frees up more bits and supposedly pretty much everyone uses today).

He then goes over 2's complement method of doing negative numbers and the easy trick to calculate it and to do arithmetic. In general for a 2's complement of a 4-bit number, if you take the example of the number 5 (0101) you invert the bits (1010) and add 1 (1011). In this case the 1011 is -5 represented in 2's complement binary. Then you can add that 2's complement number together with another number like we did before and it is like (11) + (-5) = 0, etc...

1011 +
1011 =
------
0110

11 + (-5) = 6! see, ez

Unit 2.4 - Arithmetic Logic Unit (ALU)

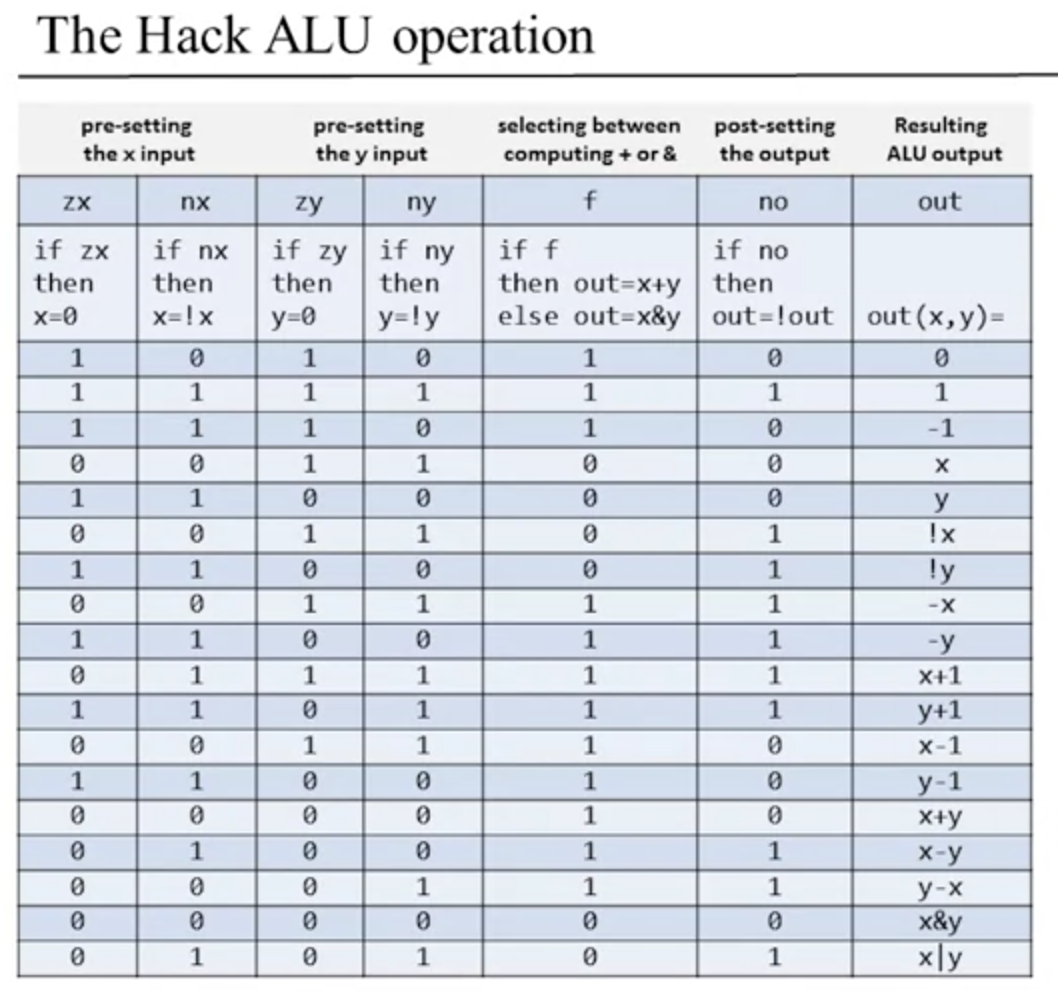
He talks about a Von Neumann architecture and how within the CPU there is the ALU. ALU takes 2 regular inputs, a 3rd input that is computed (a function input) using a family of predefined arithmetic (addition, multiplication, division, etc...) and logical (And, Or, Xor, etc...) functions. Then the outputs are the results of these functions. Here's the Hack ALU diagram and description:

two 16-bit inputs, 2's complement values
one 16-bit output, 2's complement values
six control 1-bit inputs that select which function to use (zx, nx, zy, ny, f, no)
can compute one out of a family of 18 functions
outputs two 1-bit values (zr, ng)

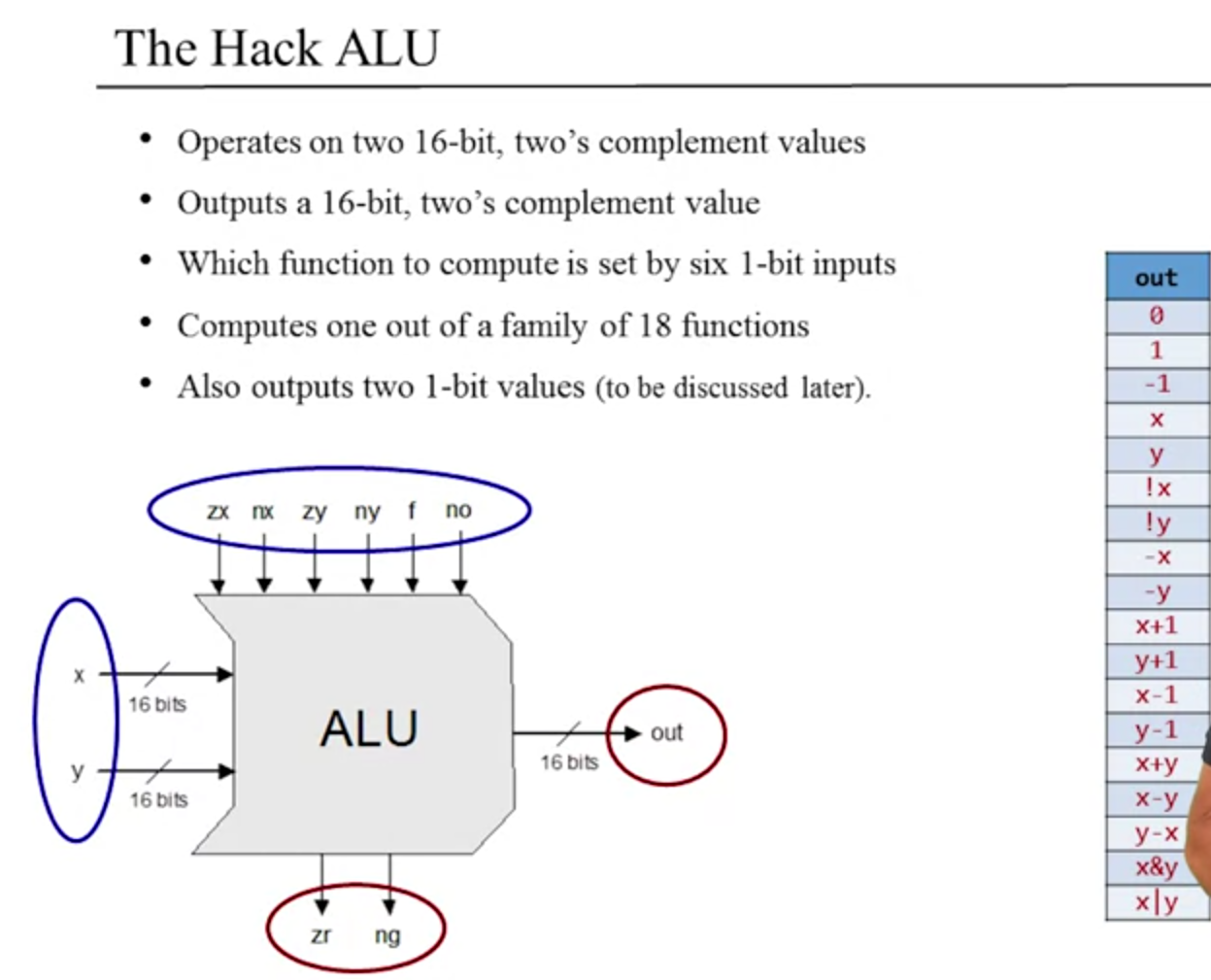
Essentially what I'm seeing is... each select bit should probably be handled by a mux or a series of mux's, the outputs describe the boolean function to do (either for arithmetic or logical operations), so like if it says x-y then i need to do an inversion on one input and add 1 to do the 2's complement subtraction, then add them together, so an add16 with a few other things being used to feed into it. for some of the others they are easy like x+1 and y+1 would just be an Inc16 for both of them. when I look at the select bits --> outputs truth table, that's where I should write out my boolean expressions and then simplify to determine how to setup the cs logic. He gives us the truth table, and in fact that is represented somewhat in the comparison file, but more abstracted since I didn't know what each of the outputs "ought" to be.

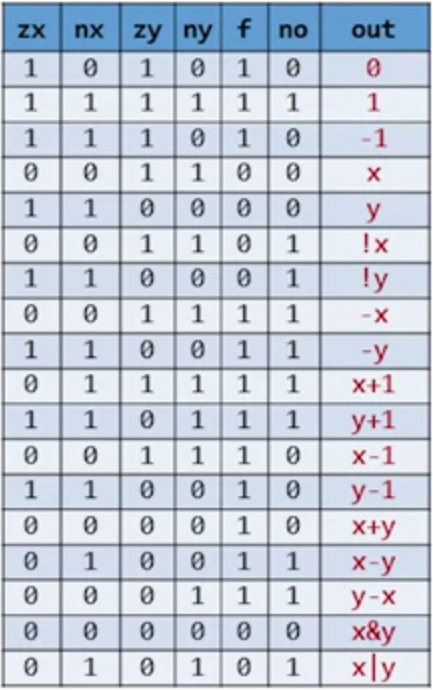
He provided an example of how to do the arithmetic operations in the hw simulator to test it:

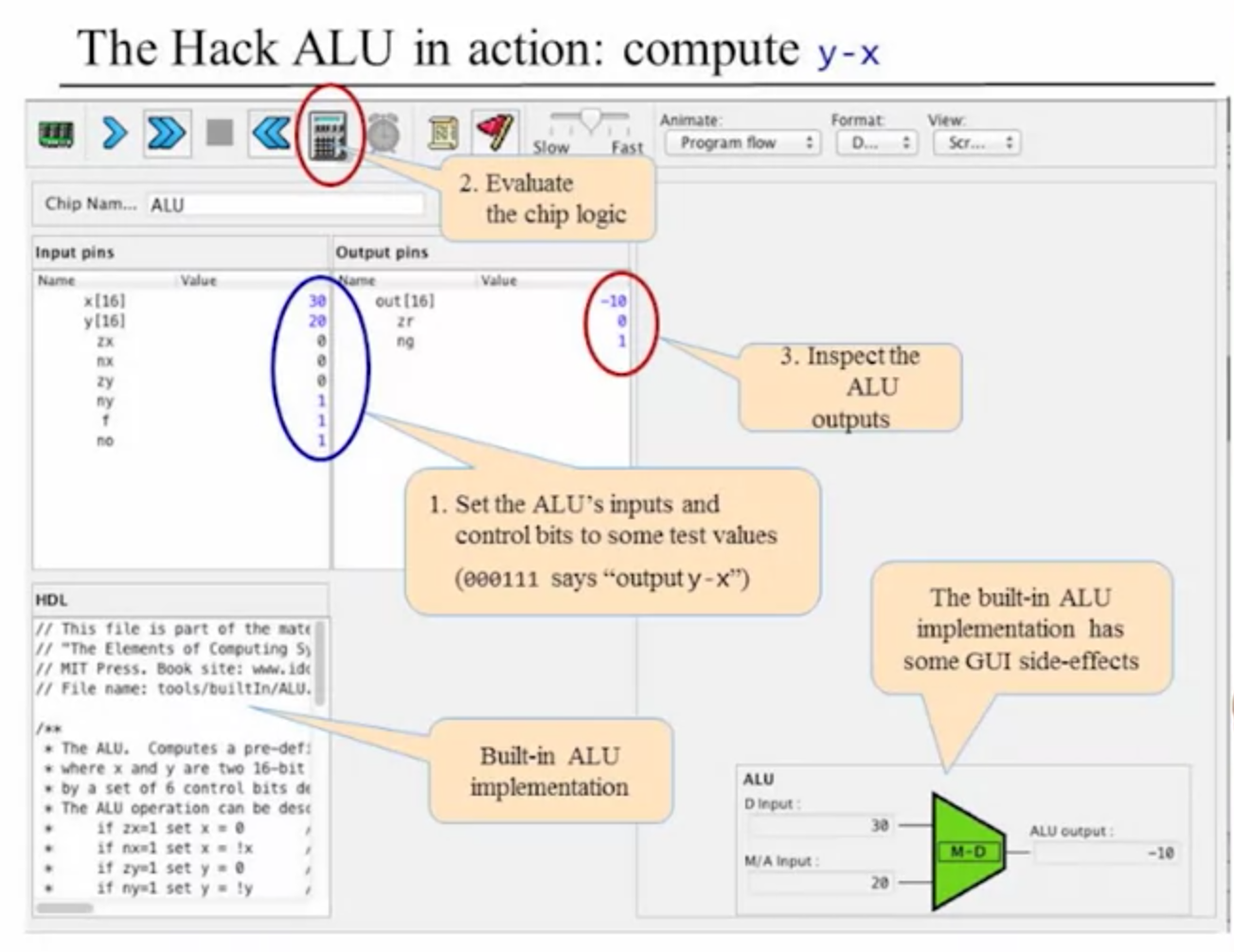
Here's the same example but boolean logic (binary i/o):

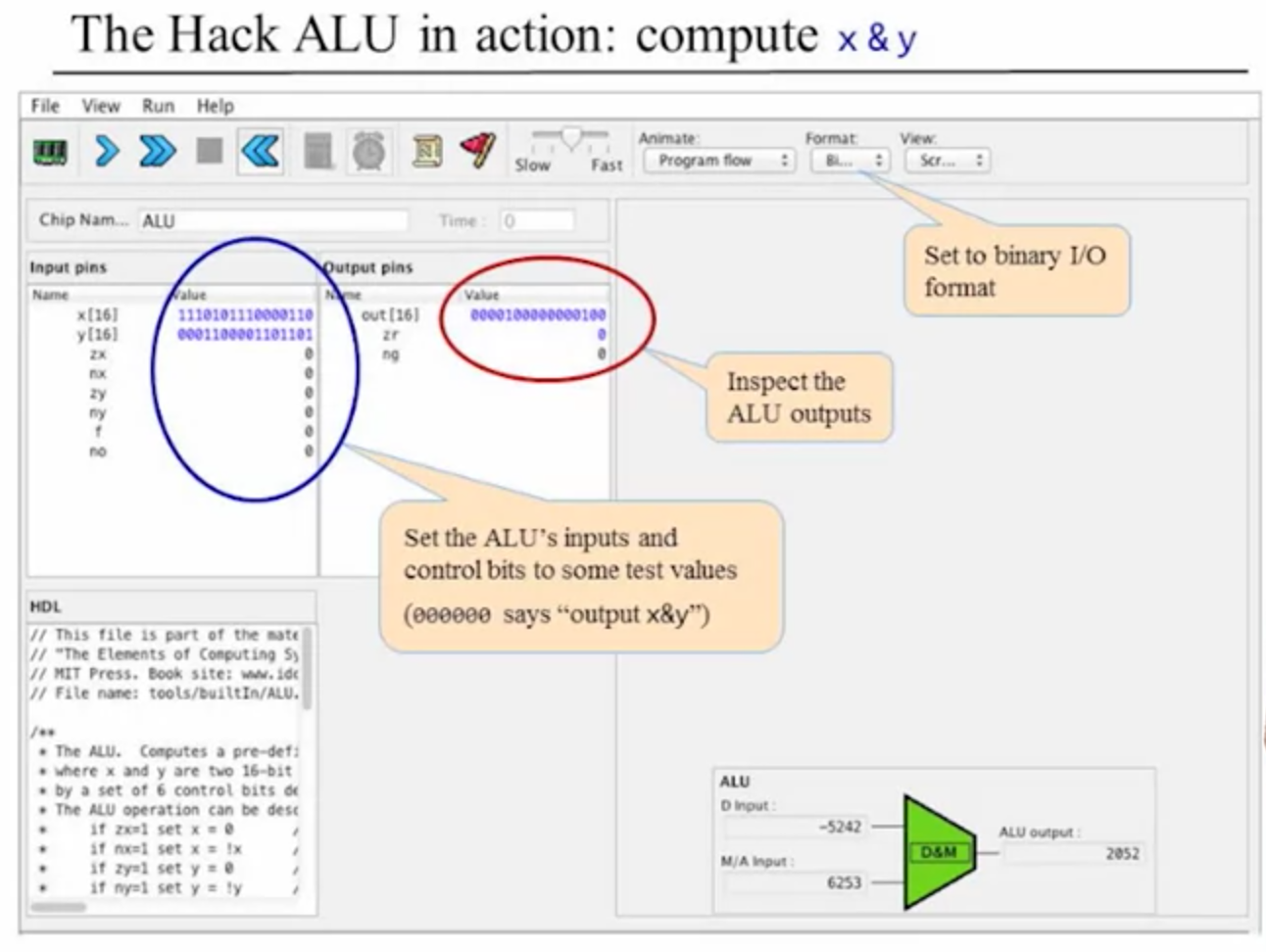
He then goes over how their ALU operates regarding the select bits and their functions.

zx - if zx is 1 then x=0 (x=false)
nx - if nx is 1 then x=!x (Not(x))
zy - if zy is 1 then y=0 (y=false)
ny - if ny is 1 then y=!y (Not(y))
f - if f is 1 then out=x+y else out=x&y (will need a mux here with one output being a fMuxAnd16 (0) and another being an fMuxAdd16 (1))
no - if no is 1 then out=!out (Not(out))
out - out(x,y)=

So he shows an operation example to compute !x

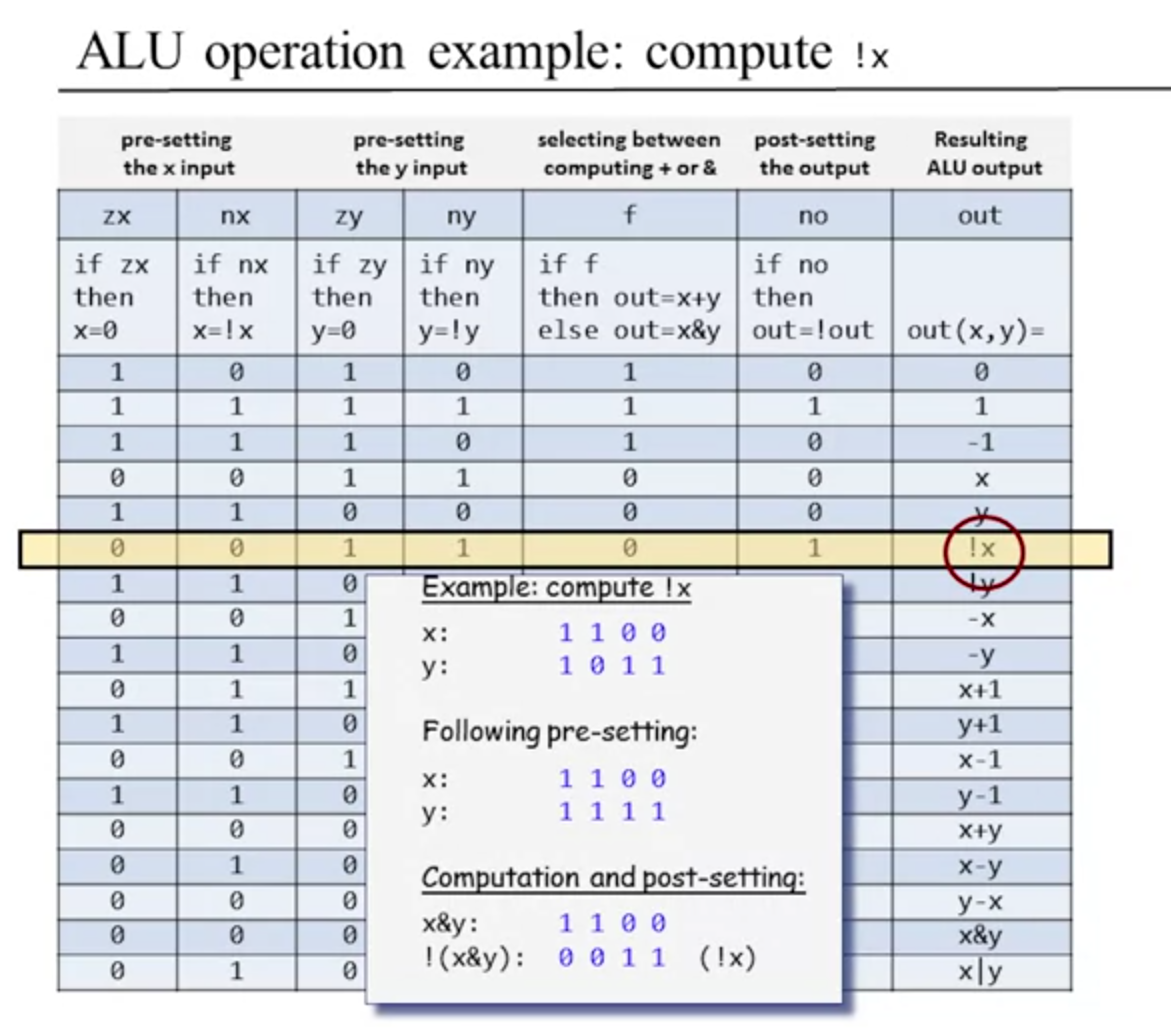
It's apparent to me that the select bits are sequential. the zy has to come before ny for some reason if both are enabled. Read the truth table from left to right for the select bits.

Another good example for y-x:

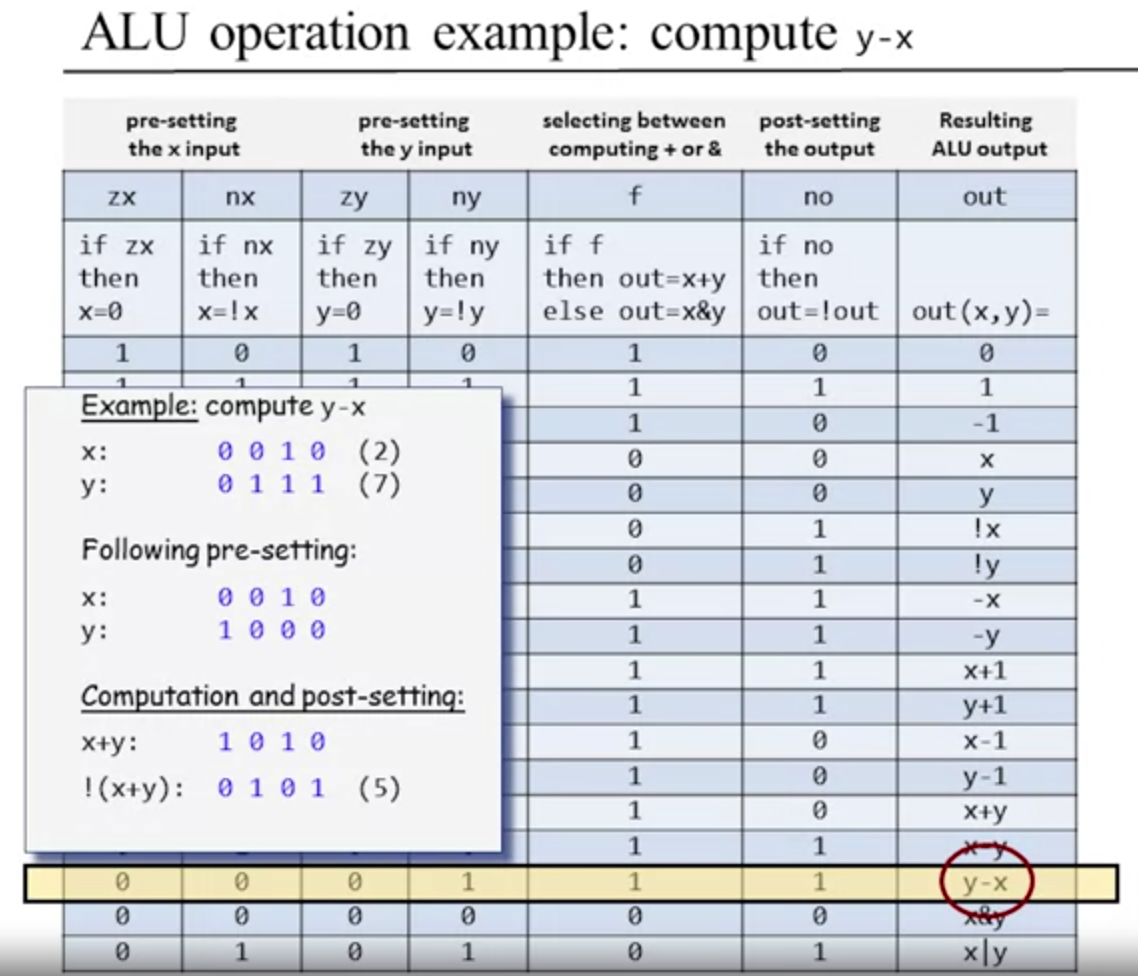
Looks like you can do 2's complement subtraction by negating y here, then adding them together, then negating the output.... so you don't need to add 1. (x) + (~y + 1) = f is also the same as ~((x) + (~y)) = f !!! Mind=blown! :P well it's just the various boolean algebra laws again at work.

They did a quiz and I passed it, it was asking what the undefined function of a combination of bits would be, and it turned out to be just 0 (out=0).

The ALU also has output control bits.

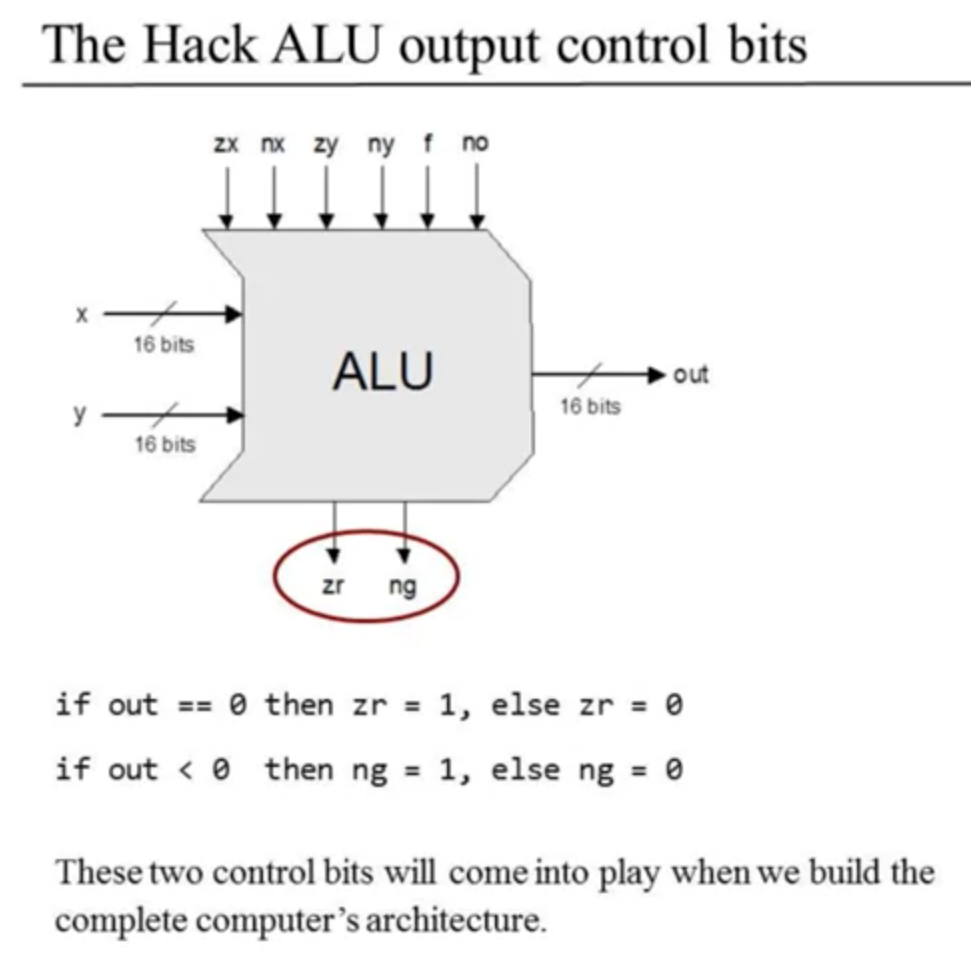
The beauty of the ALU is that we can build it from all the other chips they had me develop already. :)

Unit 2.5 - Project 2 Overview

all chips from project 1 can be used (at least the ones that match the builtin chips)
build halfadder, fulladder, add16, inc16 (completed these 4 already), and the ALU (starting on this now)

the Hack ALU truth table converted to markdown (essentially)

x[16]	y[16]	zx	nx	zy	ny	f	no	out[16]	zr	ng
16-bit input	16-bit input	x=0	x=!x	y=0	y=!y	out=x+y : x&y	out=!out	16-bit output	if out == 0	if out < 0
x	y	1	0	1	0	1	0	0	?	?
x	y	1	1	1	1	1	1	1	?	?
x	y	1	1	1	0	1	0	-1	?	?
x	y	0	0	1	1	0	0	x	?	?
x	y	1	1	0	0	0	0	y	?	?
x	y	0	0	1	1	0	1	!x	?	?
x	y	1	1	0	0	0	1	!y	?	?
x	y	0	0	1	1	1	1	-x	?	?
x	y	1	1	0	0	1	1	-y	?	?
x	y	0	1	1	1	1	1	x+1	?	?
x	y	1	1	0	1	1	1	y+1	?	?
x	y	0	0	1	1	1	0	x-1	?	?
x	y	1	1	0	0	1	0	y-1	?	?
x	y	0	0	0	0	1	0	x+y	?	?
x	y	0	1	0	0	1	1	x-y	?	?
x	y	0	0	0	1	1	1	y-x	?	?
x	y	0	0	0	0	0	0	x&y	?	?
x	y	0	1	0	1	0	1	x\|y	?	?

ng is the most difficult one to figure out for me... I need to catch for no as a selector signal, since all 2's complement negatives are inverted final outputs I think. So I'll need a mux, it's 16-bits wide, so I'll need a mux16. A positive number like 12 inverted would be 0 as the output of the most significant bit of a 4-bit wide, so the same should be true here. The problem is, if the positive number is 8 as the output, then inverting the most significant bit would read true, but that's not necessarily negative, so what gives?