The relationship between the Transpose and the Inverse of a Matrix - ben-ng/linalg GitHub Wiki

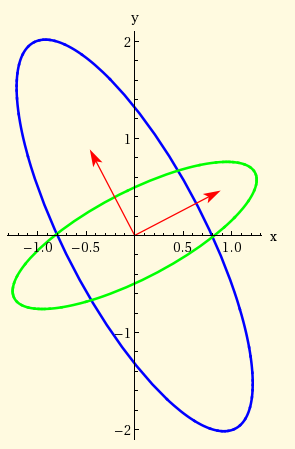
Why are the ellipses at right angles to each other?

Here's what you get when you hit the unit circle with the transpose and inverse of a matrix A.

• Transpose[A] . {Cos[t_], Sin[t_]} is in Blue
• Transpose[A^-1] . {Cos[t_], Sin[t_]} is in Green

If you did the singular value decomposition of A you'd be able to express it as hanger . stretcher . aligner.

It turns out that Transpose[A] is the same thing as Transpose[aligner] . stretcher . Transpose[hanger] and that Inverse[A] is the same thing as Transpose[aligner] . Inverse[stretcher] . Transpose[hanger].

Inverse[stretcher] can be found by replacing all non-zero diagonal entries of stretcher with their reciprocal.

It's clear that both plots are hung on the same frame -- the aligner. The long axis of one is the short axis of the other, because the stretch values in the inverse matrix are the reciprocals of the transpose's.