Logarithmic Loss - aragorn/home GitHub Wiki

• https://www.kaggle.com/wiki/LogarithmicLoss

  • The logarithm of the likelihood function for a Bernoulli random distribution.
  • 베르누이 임의 분포에 대한 우도 함수의 로그
  • In plain English, this error metric is used where contestants have to predict that something is true or false with a probability (likelihood) ranging from definitely true (1) to equally true (0.5) to definitely false(0).
  • 어떤 값이 참인지 또는 거짓인지 예측하면서, 확실히 참인지, 참 또는 거짓일 확률이 동일한지, 또는 확실히 거짓인지 확률값으로 예측할 때, 이 오류 측정 기준을 사용한다.
  • 오류에 대해 로그를 적용하는 것은 확신하거나 틀린 경우 모두에 대해 강하게 처벌하는 효과가 있다. 최악의 경우, 무엇인가 참인 것으로 확신하는 예측을 했으나 실제로는 그것이 거짓인 경우, 오류 점수에 무한대의 값을 추가하게 되며, 다른 예측값을 모두 무의미하게 만든다.

• General log loss
  
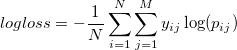
  where N is the number of examples, M is the number of classes, and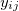 is a binary variable indicating whether class j was correct for example i.

• When the number of classes is 2 (M=2)
  

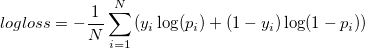
• https://www.quora.com/What-is-an-intuitive-explanation-for-the-log-loss-function

The log loss function is simply the objective function to minimize, in order to fit a log linear probability model to a set of binary labeled examples. Recall that a log linear model assumes that the log-odds of the conditional probability of the target given the features is a weighted linear combination of features . These weights are the parameters of the model which we'd like to learn.

---

Convexity

MSE(Mean Squared Error)는 logistic function 의 weight 에 대해 convex 가 아니다.

• http://bcho.tistory.com/1142
• http://www.holehouse.org/mlclass/06_Logistic_Regression.html

• Cost function for logistic regression
  • If we use this function for logistic regression this is a non-convex function for parameter optimization.

...

• Why do we chose this function when other cost functions exist?
  • This cost function can be derived from statistics using the principle of maximum likelihood estimation.
    • Note this does mean there's an underlying Gaussian assumption relating to the distribution of features.
  • Also has the nice property that it's convex.

• How to prove that logistic loss is a convex function? https://math.stackexchange.com/questions/2458438/convexity-of-logistic-loss
• Why is the error function minimized in logistic regression convex? http://mathgotchas.blogspot.kr/2011/10/why-is-error-function-minimized-in.html
• Why is a cross-entropy loss function convex for logistic regression, but not for neural networks? https://www.quora.com/Why-is-a-cross-entropy-loss-function-convex-for-logistic-regression-but-not-for-neural-networks