Trees

What?

• An oriented acyclic and weakly connected graph that starts with a root and only has one path to reach another node
• Recursive Definition => A tree is a root node pointing to trees, which themselves point to other trees
• Each node contains unique information

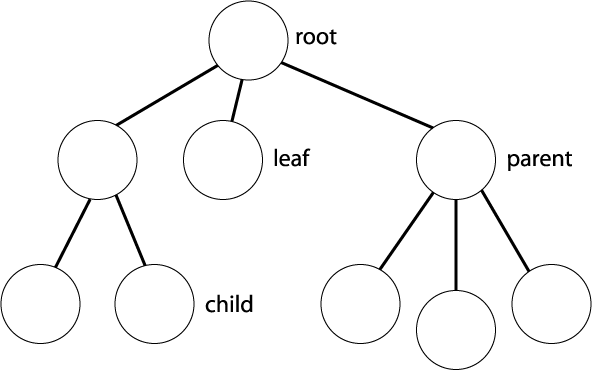
Terminology

• Parent => Node Immediately predecessor of another
• Child => Node Immediately successor of another
• Root => Node that has no parent
• Leaf => Node that has no child
• Ancestor(s) => All nodes that are predecessors to a node up to the root
• Descendant(s) => All nodes that are successors to a node up to its accessible leafs
• Height of a node => Length of longest path to reach a leaf from a node
• Height of the tree => Height of the root node
• Node depth => Length of a path from the root to the node
• Node degree => Number of children a node has
• Sub-tree => Tree composed from a bigger tree...

Types

• Degenerate tree => A simply linked list is a tree of degree 1
• Binary Tree => Of degree 2
• Binary Search Tree => All keys must be different at all time. The left sub-tree of a node must contain strictly lower values and the right sub-tree of a node must contain strictly higher values

• Self Balancing Binary Search Tree(AVL) => For each node, the difference between height of the its right sub-tree and its left sub-tree is equal or less than 1. Searching in O(Logn)
• N-ary tree => A tree of degree N

Tree Traversal

• Pre-order => Priority is to the parent. Children comes after.
• Post-order => Priority to the children. Parent(root) comes after
• In-order(symmetric) => Left child, root, right child... Gives us elements in order from smallest to biggest

Expression Tree

• Leafs are operands(variables or constants) and internal nodes are operators. A calculation can be reconnected with In-order traversal

Implementations

• 2 major implementations => In a table and by chaining

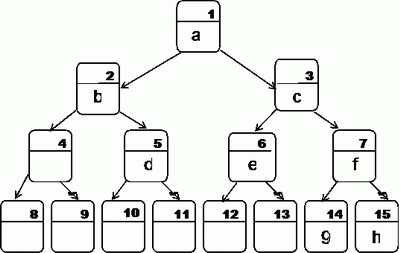
Binary Tree Table

• Index starts at 1 with the root

• Contains up to 2^h nodes

• Advantages =>

  • Simple to visit children
  • No memory to store pointers
  • Memory to insert a node is already available

• Disadvantage =>

  • Memory wasted for holes
  • Re-allocation is higher if node is outside the boundaries of the existing table

• Tree is a heap =>

  • When Binary Tree is complete except maybe the last level where the missing nodes are to the right.
  • Node value is always bigger than or equal to the value of its children(Max Heap) see Heap for prioritize implementation

Binary Search Tree

• Use to implement dictionaries => Efficient for Insertions, Suppressions, Finding
• Keep elements in order with symmetric traversal
• The 3 basic operations have a complexity of O(logN)

By Chaining

• Keeps a pointer of both children

• Advantages =>

  • Size of the tree is dynamic
  • Easy to operate on pointers

• Disadvantage =>

  • Keep an eye on double references and memory leaks
  • Tree traversal goes from root to leafs only. Can go the other way with recursion

• With AVL, equilibrium must be maintained... It must be rebalanced if it ain't so

• AVL complexities =>

  • Leaf insertion => O(1)
  • Balancing verification => O(1)
  • Update height of a node => O(1)
  • Balancing(zigZag) => O(1)
  • Find insertion point => O(log n)
  • Be at the critical node for balancing => O(log n)
  • Node insertion => O(log n)
  • Node Removing => O(log n)
  • Finding Node => O(log n)