Bellman-Ford Algorithm

Execution time will be more costly than Dijkstra, but this algorithm treats negative values

General Algorithm

• Negative length cycles => Bellman-Ford does a check to make sure it does not happen, which is not the case in Dijkstra implementations

• Complexity => O(nm)

// Initialize each node cost and node predecessor
foreach node in GRAPH.nodes
    node.cost = INFINITY
    node.predecessor = NIL

// source node has no predecessor...
SOURCE.predecessor = 0

// Loop through all the nodes in the graph
for (GRAPH.nodes - 1).times

    // Loop through all the arcs of the graph
    for arc in GRAPH.arcs

        // Calculate temporary value of the arc P.S.: value and cost are synonyms
        temp = arc.source.cost + arc.weight

        // If new value is less than the one before on destination node i.e. relaxation...
        if temp < arc.destination.cost

            // Update to the new lower cost
            arc.destination.cost = temp

            // Set the predecessor to the arc's source
            arc.destination.predecessor = arc.source

// Verify if there is a negative cycle present
for arc in GRAPH.arcs

    // Return false if cost of destination of the arc is bigger than
    // cost of source of the arc plus the arc's weight
    if arc.destination.cost > arc.source.cost + arc.weight
        return FALSE
    
    // otherwise
    return TRUE          

With Acyclic Graphs

• Topologic Order => Visiting nodes in topologic order. Ex: c, s, a, b, d

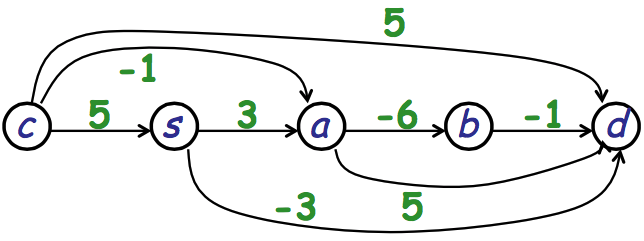
• Reduce Relaxation => This allows us to not have to relax the same arc multiple times.
• Complexity => Worst case O(n2)

1. Identify all nodes with entrance arity degree of 0
2. Puts these nodes at the beginning of the table(list)
3. Get rid of the exit arc of these nodes from the table
4. Start over again with the new graph
5. OPTIMISATION TRICK =>  Only visit adjacent node from removed nodes See this page

// Initialize each node cost and node predecessor
foreach node in GRAPH.nodes
    node.cost = INFINITY
    node.predecessor = NIL

// source node has no predecessor...
SOURCE.predecessor = 0

// Call Topological sorting
(result, SORTED_INDEDREE_LIST) = topologicalSorting(GRAPH, GRAPH.nodes.indegrees)

// Return false if there is a cycle detected
if result == FALSE

    return FALSE

// from 1 to to the number of nodes in the graph
for index in GRAPH.nodes.end
    
    // Get the next node in the sorted indegree list
    current_node = SORTED_INDEDREE_LIST[index]
    
    // All the adjacent nodes to the current 0 indegree node
    for adjacent to current_node
        
        // Temporary cost to evaluate
        temp = current_node.cost + arc(current_node, adjacent).weight
        
        // Relaxation
        if temp < adjacent.cost
            
            // Update cost of adjacent node
            adjacent.cost = temps
            
            // Update shortest path predecessor to adjacent
            adjacent.predecessor = current_node

return TRUE

• Complexity => In this state, Bellman-Ford execute in O(n+m)