Graph Algorithms - ZheWang711/Notebook_Algo GitHub Wiki
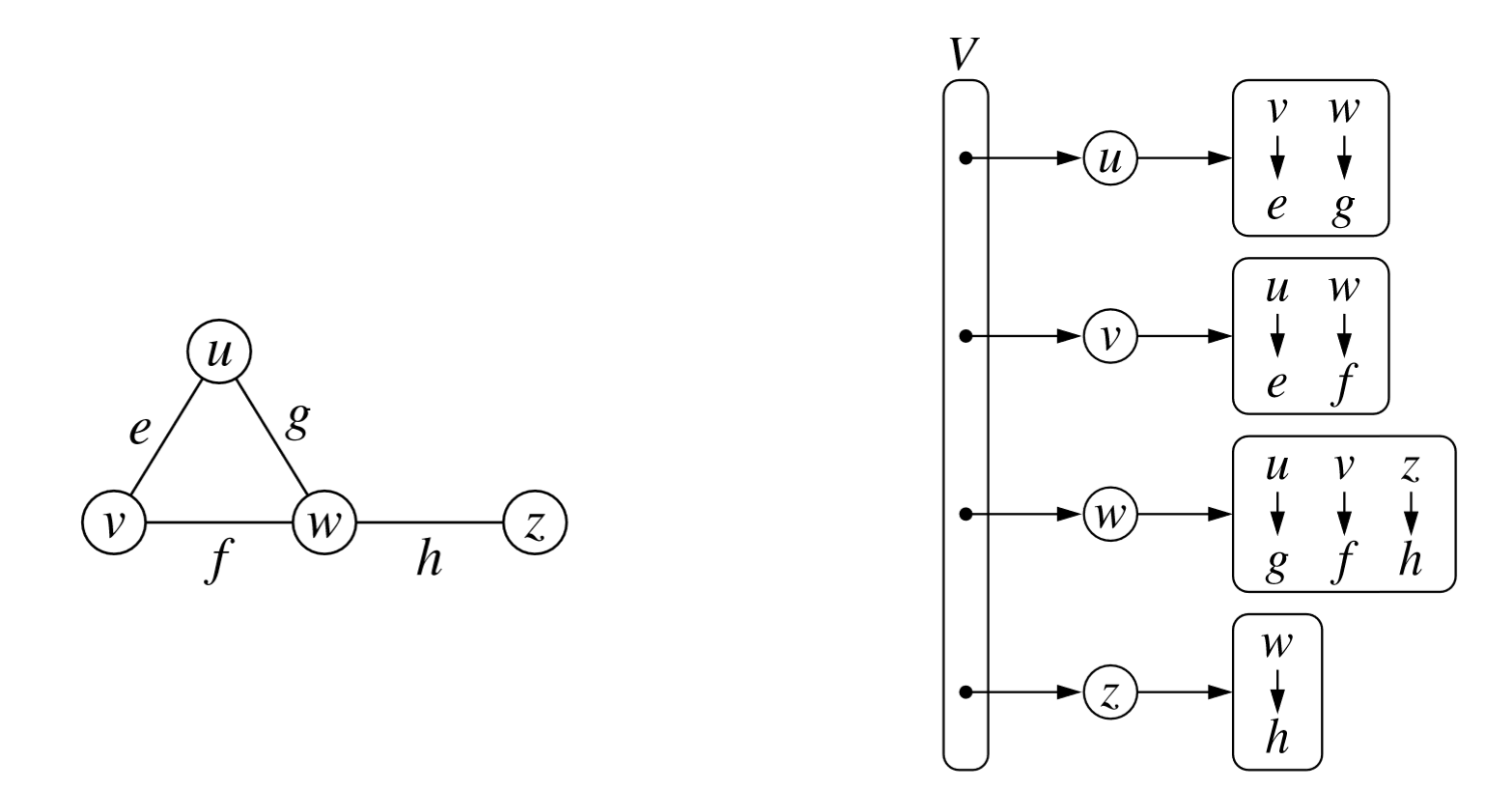
Specifically, for each vertex v, we maintain a collection I(v), called the incidence collection of v, whose entries are edges incident to v. In adjancy map, we use a hash-based map (Python Dictionary) to implement I(v).
For each vertex v.
Let the opposite endpoint of each incident edge serve as a key in the map, with the edge structure serving as the value.
self._outgoing = {} # only create second map for directed graph; use alias for undirected
self._incoming = {} if directed else self. outgoingself._outgoing[new_vertex] = {}
if self.isdirected:
self._incoming[new_vertex] = {}self._outgoing[tail][head] = new_edge
self._incoming[head][tail] = new_edgedel self._outgoing[tail][head]
del self._incoming[head][tail]del self._outgoing[v]
for edge_map in self._outgoing.values: # delete all edges coming towards v in self._outgoing
if edge_map.get(v) is not None:
del edge_map[v]
if self.isdirected:
del self._incoming[v]
for edge_map in self._incoming.values: # delete all edges going out from v in self._incoming
if edge_map.get(v) is not None:
del edge_map[v]- Performance
Assuming m is the number of edges, and n is the number of vertices.
| Operation | Rumming Time Complexity |
|---|---|
| Insert Vertex | O(1) |
| Insert Edge | O(1) exp. |
| Remove Vertex | O(dv ) |
| Remove Edge | O(1) exp. |
Cut: A cut of graph (V, E) is a partition of V into two non-empty sets A and B.
Crossing Edges: those edges with
- one endpoint in each of (A, B) [undirected]
- tail in A and head in B [directed]
Problem
- INPUT: An directed graph G = (V, E), woth parallel edges allowed
- GOAL: Compute a aut with fewest number of crossing edges
- Applications:
- identify network bottlenecks / weakness
- image segmentation
- community detection in social networks
while there are more than 2 vertices:
pick a remaining edge (u, v) uniformly at random
merge (contract) u and v into a single vertexd
remove self-loops
return cut represented by final 2 vertices
Full implementation in Python, using union-set to improve the performance.
- Using union-set to represent "large vertices".
- Maintain a list to remember vertices/sets that are not merged yet
-
merge: when two vertices are mergering (randomly choosing 2 'vertices' from the vertices/sets list then remove them from the list) ,unionthe corresponding vertices, then add the new vertex into the list. -
remove self loop: Maintain a variable to remember the number of 'eliminating' edges during merging process when two vertices are merging, the number of 'eliminating edges' is the count of edges crossing the two sets (one node in set A, the other node in set B)
Suppose:
Cut is (A, B) is one of the correct answer.
F is the set of edges crossing A and B.
Si is the event that an edge of F is is contracted in iteration i. k is the number of edges crossing A and B. m is the number of edges. n is the number of vertices.
P[output is A and B] = P[never contracts an edge of F] = P[ S(1) and S(2) and ... and S(n-1)]
m >= 0.5 * k * n
Proof:
- Consider each vertex as a cut (i.e. cut{v}, cut{G-v}), since k is min cut number ,
then we have
degree[v] >= kfor each vertex v. - The sum of degree for each vertex, SUM, in G, we have
SUM >= knandSUM = 2 * m - Combine the 2 equations in step 2, we have
m >= 0.5 * k * n, QED.

Summary
| Iteration Time | Pr[all fall] |
|---|---|
| n^2 | 1/e |
| n^2ln(n) | 1/n |
The BFS algorithm can explore the vertices that are reachable from source s layer by layer. It can compute the connected components of undirected graphs, and the distance from s to each reachable vertices.
Running time O(m + n).
The main part of BFS algorithm is a while loop, which maintain a queue Q to manage the set of frontier vertices(the explored vertices that have not yet had there adjacency list fully explored).
Loop invariant: At each begin time of the while loop the queue Q consists of the set of frontier vertices.
BFS(G, s):
mark all vertices in G unexplored
mark s as explored
s.d = 0
s.pi = None
Q = queue(s)
while Q is not empty:
u = Q.deque()
for each v in u.neighbours():
if v is not explored:
v.explore()
v.d = u.d + 1
v.pi = u
- During execution, BFS discovers every vertex
vin V that are reachable froms - Upon termination, for each
vin V that are reachable froms,v.d= distance fromstov. - During the execution of BFS, we define a predecessor subgraph G' of G, where G' = (V', E'); and V' = {v in V where v.pi != None} U {s}, and E' = {(v.pi, v): v in V' -{s}}. The subgraph G' is a breadth first tree: V' consists all vertices reachable from
sand G' contains a unique simple path fromstovthat is also a shortest path fromstovin G.
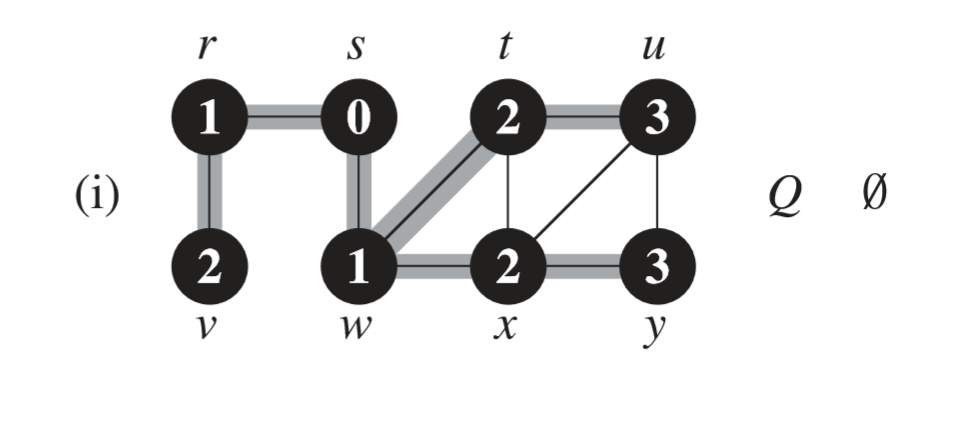
def connecting_components(self):
cnt = 1
for i in self.outgoing.keys():
if not i.is_explored:
print("component {0}".format(cnt))
self.BFS(i)
cnt += 12 time stamps (implemented by global variable) for each vertex:
-
u.d: the time when the vertex is discovered. -
u.f: the time when the vertex is finished explored (all adjacent vertices are finished).
2 means of implementation:
- using stack
def DFS(self, source):
"""
Depth first search using stack
:param source: the source vertex object
reference: http://www.egr.unlv.edu/~larmore/Courses/CSC477/bfsDfs.pdf
This DFS Algorithm maintain a stack S, whose values are tuples, with
(vertex v, a list a unexplored neighbour vertices of v).
Vertex v is in the stack if and only if there is at least one neighbour of v that is remain unexplored
"""
time = 1
source.d = time
print('time {0}: vertex {1} discover'.format(source.d, source.id))
source.is_explored = True
S = [(source, randomize(list(self.outgoing[source].keys())))]
while len(S) != 0:
vertex, neighbours = S.pop()
if len(neighbours) == 0:
time += 1
vertex.f = time
print('time {0}: vertex {1} finished'.format(vertex.f, vertex.id))
if len(neighbours) != 0:
tmp = neighbours[0]
del neighbours[0]
S.append((vertex, neighbours))
tmp.is_explored = True
tmp_neighbours = randomize([ver for ver in self.outgoing[tmp].keys() if not ver.is_explored])
S.append((tmp, tmp_neighbours))
time += 1
tmp.d = time
print('time {0}: vertex {1} discover'.format(tmp.d, tmp.id))- recursive implementation
def DFS_r(self, source):
"""
Depth first search recursive implementation
"""
source.d = self.time
self.time += 1
source.d = self.time
source.is_explored = True
print('time {0} discover {1}'.format(source.d, source.id))
for i in self.outgoing[source].keys():
if not i.is_explored:
self.DFS_r(i)
self.time += 1
source.f = self.time
print('time {0} finish {1}'.format(source.f, source.id))DFS-loop(G):
mark all nodes as unexplored
current_label = n [to keep track of the ordering]
for each vertex
if v not yet explored:
DFS(G, v)
DFS(G, s):
for every edge (s, v):
if v not yet explored
mark v explored
DFS(G, v)
set f(s) = current_label
current label -= 1