K均值聚类算法（K-Means）

K-Means是一种常见的基于划分的聚类算法，其划分方法的基本思想是：给定一个有N个元组或者记录的数据集，将数据集依据样本之间的距离进行迭代分裂，划分为K个簇，其中每个簇至少包含一条实验数据

步骤

1. 先定义总共有多少个类/簇（cluster）
2. 将每个簇心（cluster centers）随机选定在该簇的某个点上
3. 将每个数据点关联到最近簇中心所属的簇上
4. 对于每一个簇，找到其所有关联点的中心点（对该簇的每一个点的坐标取平均值）
5. 将步骤4中得到的点作为新的簇心
6. 不停的重复上述步骤，直到每个簇所拥有的的点不变

示例

题目：有6个点，将A3和A4作为两个簇的初始簇心，问最终簇的归属情况

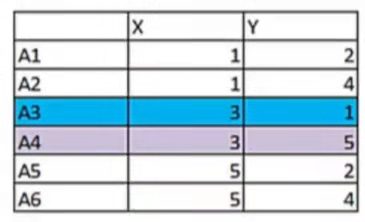
1. 先定义总共有多少个类/簇（cluster） 已经确定了将数据分为两簇
2. 将每个簇心（cluster centers）随机选定在该簇的某个点上 已经定义A3和A4位两簇数据的簇心
3. 将每个数据点关联到最近簇中心所属的簇上 根据距离公式（可以是欧几里得距离、曼哈顿距离等），计算每个点到簇心的距离，将距离近的点归为一类【归类时不涉及原簇心】
   
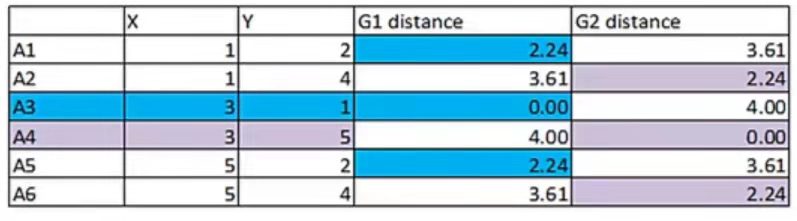
4. 对于每一个簇，找到其所有关联点的中心点（对该簇的每一个点的坐标取平均值）
   
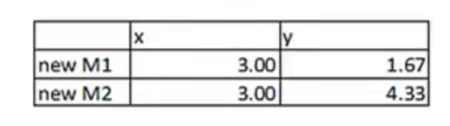
5. 将步骤4中得到的点作为新的簇心 于是可以得到新簇心，（3.00,1.67）和（3.00,4.33）
6. 不停的重复上述步骤，直到每个簇所拥有的的点不变 再次计算每个点到簇心的距离并将距离近的点归为一类
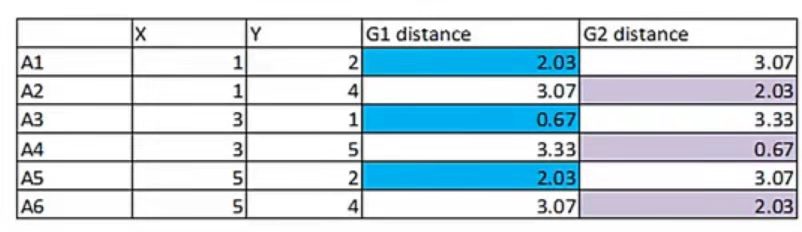   由于关联点较第一次没有变化，所以之后的计算结果也不会改变，因此停止计算 得到两簇数据：a:A1/A3/A5；b:A2/A4/A6，其簇心为（3.00,1.67）；（3.00,4.33）

MATLAB程序

MATLAB中使用kmeans函数来实现K均值聚类
可以参考"https://ww2.mathworks.cn/help/stats/kmeans.html#namevaluepairarguments"

%% 随机生成两簇数据并绘制出来
X = [randn(100,2)*0.75+ones(100,2);
    randn(100,2)*0.5-ones(100,2)];
figure;
plot(X(:,1),X(:,2),'.');
title 'Randomly Generated Data';

%% K均值聚类处理
%K均值聚类相关参数的处理及kmeans函数
opts = statset('Display','final');   %'final'——显示最终迭代的结果
[idx,C] = kmeans(X,2,'Distance','cityblock','Replicates',5,'Options',opts);   %'cityblock'——曼哈顿距离；‘5’——迭代次数
%idx——与 X 中的观测值对应的预测簇索引的向量
%C——聚类最终的质心位置

figure;
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12)
hold on
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12)
plot(C(:,1),C(:,2),'kx','MarkerSize',15,'LineWidth',3) 
legend('Cluster 1','Cluster 2','Centroids','Location','NW')
title 'Cluster Assignments and Centroids'
hold off