遗传算法&TSP的问题介绍

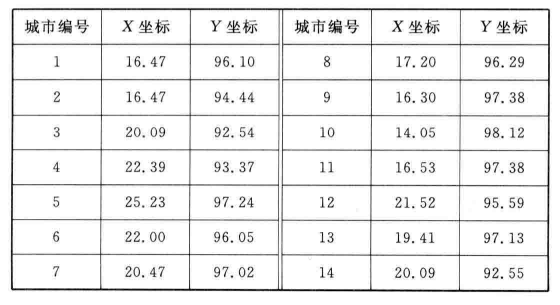
本案例以14个城市为例，假定14个城市的位置坐标如表所列，寻找出一条最短的遍历14个城市的路径

算法步骤

算法流程图

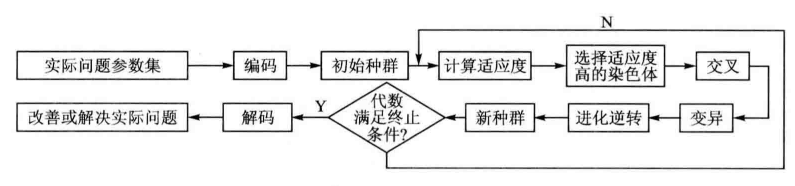
算法步骤

1. 编码
   采用整数排列编码方法。对于 n 个城市的 TSP 问题,染色体分为n段,其中每一段为对应城市的编号,如对 10 个城市的 TSP 问题{1,2,3,4,5,6,7,8,9,10},则 11 | 10 | 2 1 4 1 5 1 6 1 8 1 7 1 9 1 3 就是一个合法的染色体。

2. 种群初始化
   在完成染色体编码以后,必须产生一个初始种群作为起始解,所以首先需要决定初始化种群的数目。初始化种群的数目一般根据经验得到,一般情况下种群的数量视城市规模的大小而确定,其取值在 50～200 之间浮动。

3. 适应度函数
   设 k1 | k2 | … | ki |…| kn |为一个采用整数编码的染色体,D_kikj为城市ki到城市kj,的距离,则该个体的适应度为
   
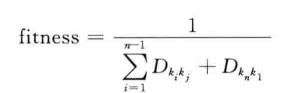
   即适应度函数为恰好走遍π个城市,再回到出发城市的距离的倒数。优化的目标就是选择适应度函数值尽可能大的染色体,适应度函数值越大的染色体越优质,反之越劣质。

4. 选择操作
   选择操作即从旧群体中以一定概率选择个体到新群体中,个体被选中的概率跟适应度值有关,个体适应度值越大,被选中的概率越大。

5. 交叉操作
   采用部分映射杂交,确定交叉操作的父代,将父代样本两两分组,每组重复以下过程(假定城市数为 10)：
   ①产生两个[1,10]区间内的随机整数r1和r2,确定两个位置,对两位置的中间数据进行交叉,如r1=4,r2=7
   
   交叉为
   
   ②交叉后,同一个个体中有重复的城市编号,不重复的数字保留,有冲突的数字(带*位置)采用部分映射的方法消除冲突,即利用中间段的对应关系进行映射。结果为
   

6. 变异操作
   变异策略采取随机选取两个点,将其对换位置。产生两个[1,10]范围内的随机整数r1和r2,确定两个位置,将其对换位置,如r1=4,r2=7
   
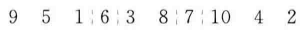
   变异后为
   

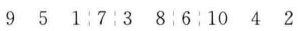
7. 进化逆转操作
   为改善遗传算法的局部搜索能力,在选择、交叉,变异之后引进连续多次的进化逆转操作。这里的“进化”是指逆转算子的单方向性,即只有经逆转后,适应度值有提高的才接受下来,否则逆转无效。
   产生两个[1,10]区间内的随机整数r1和r2,确定两个位置,如r1=4,r2=6，算出它们之间的基因数中最大的数和最小的数，然后将它们之间的数作为向量，按两数中的大数排序至小数（即当大的数是位置靠后的数，则进行反向排序，否则正常排序）
   
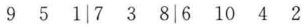
   进化逆转后为
   
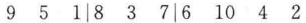
   对每个个体进行交叉变异,然后代人适应度函数进行评估,选择出适应值大的个体进行下一代的交叉和变异以及进化逆转操作。循环操作:判断是否满足设定的最大遗传代数 MAXGEN,不满足则跳入适应度值的计算;否则,结束遗传操作。

MATLAB程序

1 初始化参数（包括遗传算法参数）

X =[16.47,96.10
    16.47,94.44
    20.09,92.54
    22.39,93.37
    25.23,97.24
    22.00,96.05
    20.47,97.02
    17.20,96.29
    16.30,97.38
    14.05,98.12
    16.53,97.38
    21.52,95.59
    19.41,97.13
    20.09,92.55];%个城市坐标位置,可以换成load CityPosition1.mat
NIND=100;       %种群大小
MAXGEN=200;
Pc=0.9;         %交叉概率
Pm=0.05;        %变异概率
GGAP=0.9;      %代沟(Generation gap)
D=Distanse(X);  %生成距离矩阵
N=size(D,1);    %(34*34)

2 种群初始化

• Chrom=InitPop(NIND,N);：主函数中的语句，调用InitPop函数来生成初始种群

InitPop函数

function Chrom=InitPop(NIND,N)
Chrom=zeros(NIND,N);%用于存储种群
for i=1:NIND
    Chrom(i,:)=randperm(N);%随机生成初始种群
end

3 计算每种路线的适应度

ObjV=PathLength(D,Chrom);  %计算路线长度
FitnV=Fitness(ObjV);    % 每种路线的适应度

Fitness函数

function FitnV=Fitness(len)
FitnV=1./len;

• 取每条路线的长度的倒数作为适应度，从而路线长度越短，适应度越大，染色体的个体越优

4 选择

• SelCh=Select(Chrom,FitnV,GGAP);：主函数的语句，调用Select函数从旧群体选择几个个体到新群体中，这里用到的是随机普遍取样法（Stochastic Universal Sampling）

Select函数

function SelCh=Select(Chrom,FitnV,GGAP)
NIND=size(Chrom,1);
NSel=max(floor(NIND*GGAP+.5),2);
ChrIx=Sus(FitnV,NSel);
SelCh=Chrom(ChrIx,:);

• 其中先得到需要选择的染色体个体个数，然后调用Sus函数使用随机普遍取样法进行选择

Sus函数

function NewChrIx = Sus(FitnV,Nsel)

% Identify the population size (Nind)
   [Nind,ans] = size(FitnV);

% Perform stochastic universal sampling
   cumfit = cumsum(FitnV);
   trials = cumfit(Nind) / Nsel * (rand + (0:Nsel-1)');
   Mf = cumfit(:, ones(1, Nsel));
   Mt = trials(:, ones(1, Nind))';
   [NewChrIx, ans] = find(Mt < Mf & [ zeros(1, Nsel); Mf(1:Nind-1, :) ] <= Mt);

% Shuffle new population
   [ans, shuf] = sort(rand(Nsel, 1));
   NewChrIx = NewChrIx(shuf);

5 交叉

• SelCh=Recombin(SelCh,Pc);：主函数中的语句，调用Recombin函数进行交叉，这里采用部分映射交叉

Recombin函数

function SelCh=Recombin(SelCh,Pc)
NSel=size(SelCh,1);
for i=1:2:NSel-mod(NSel,2)
    if Pc>=rand %交叉概率Pc
        [SelCh(i,:),SelCh(i+1,:)]=intercross(SelCh(i,:),SelCh(i+1,:));
    end
end

• 先选择进行交叉的两个位置，然后调用intercross函数进行部分映射交叉

intercross函数

function [a,b]=intercross(a,b)
L=length(a);
r1=randsrc(1,1,[1:L]);
r2=randsrc(1,1,[1:L]);
if r1~=r2
    a0=a;b0=b;
    s=min([r1,r2]);
    e=max([r1,r2]);
    for i=s:e
        a1=a;b1=b;
        a(i)=b0(i);
        b(i)=a0(i);
        x=find(a==a(i));
        y=find(b==b(i));
        i1=x(x~=i);
        i2=y(y~=i);
        if ~isempty(i1)
            a(i1)=a1(i);
        end
        if ~isempty(i2)
            b(i2)=b1(i);
        end
    end
end

6 变异

• SelCh=Mutate(SelCh,Pm);：主函数中的语句，调用Mutate函数进行变异操作，这里将染色体个体的两个元素的位置交换作为变异手段

Mutate函数

function SelCh=Mutate(SelCh,Pm)
[NSel,L]=size(SelCh);
for i=1:NSel
    if Pm>=rand
        R=randperm(L);
        SelCh(i,R(1:2))=SelCh(i,R(2:-1:1));
    end
end

7 进化逆转操作

• SelCh=Reverse(SelCh,D);：主函数中的语句，调用Reverse函数进行进化逆转操作，即产生两个基因变量区间内的随机整数，算出它们之间的基因数中最大的数和最小的数，算出它们之间的基因数中最大的数和最小的数，然后将它们之间的数作为向量，按两数中的大数排序至小数（即当大的数是位置靠后的数，则进行反向排序，否则正常排序），只有经逆转后,适应度值有提高的才接受下来,否则逆转无效

Reverse函数

function SelCh=Reverse(SelCh,D)
[row,col]=size(SelCh);
ObjV=PathLength(D,SelCh);  %计算路径长度
SelCh1=SelCh;
for i=1:row
    r1=randsrc(1,1,[1:col]);
    r2=randsrc(1,1,[1:col]);
    mininverse=min([r1 r2]);
    maxinverse=max([r1 r2]);
    SelCh1(i,mininverse:maxinverse)=SelCh1(i,maxinverse:-1:mininverse);
end
ObjV1=PathLength(D,SelCh1);  %计算路径长度
index=ObjV1<ObjV;
SelCh(index,:)=SelCh1(index,:);

8 子代插入种群中

• Chrom=Reins(Chrom,SelCh,ObjV);：主函数中的语句，调用Reins函数将子代插入种群中

Reins函数

function Chrom=Reins(Chrom,SelCh,ObjV)
NIND=size(Chrom,1);
NSel=size(SelCh,1);
[TobjV,index]=sort(ObjV);
Chrom=[Chrom(index(1:NIND-NSel),:);SelCh];

解

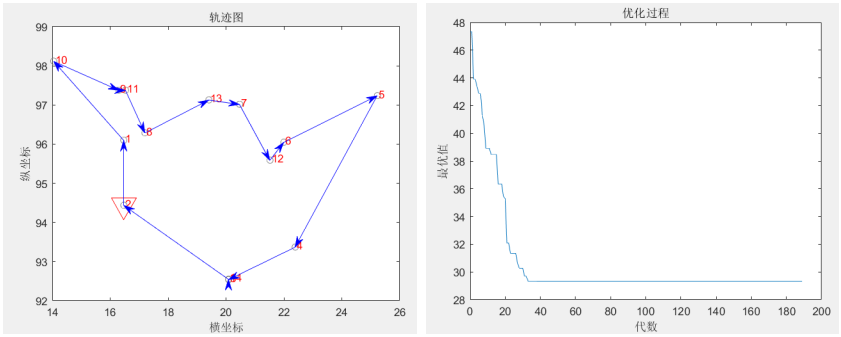
最优解:
2—>1—>10—>9—>11—>8—>13—>7—>12—>6—>5—>4—>3—>14—>2
总距离：29.3405