1 遗传算法与非线性规划的寻优算法

• 经典的非线性规划算法大多采用梯度下降的方法求解，局部搜索能力较强，但是全局搜索能力较弱
• 遗传算法采用选择、交叉和变异算子进行搜索，全局搜索能力较强，但是局部搜索能力较弱，所以一般只能得到问题的次优解，而非最优解
• 因此，通过结合两种算法的优点：一方面采用遗传算法进行全局搜索；一方面采用非线性规划算法进行全局搜索，从而可以得到问题的最优解

2 算法步骤

2.1 算法流程图

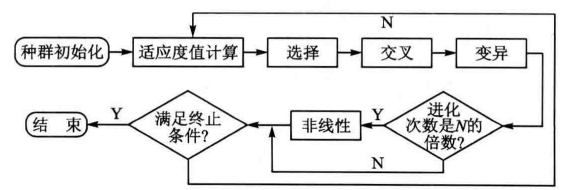
其中,种群初始化模块根据求解问题初始化种群,适应度值计算模块根据适应度函数计算种群中染色体的适应度值,选择、交叉和变异为遗传算法的搜索算子,N 为固定值,当进化次数为 N 的倍数时,则采用非线性寻优的方法加快进化,非线性寻优利用当前染色体值采用函数fmincon寻找问题的局部最优值。

2.2 算法步骤

1. 种群初始化

• 由于遗传算法不能直接处理问题空间的参数，因此必须通过编码把要求问题的可行解表示成遗传空间的染色体或者个体。
• 常用的编码方法有位串编码、Grey 编码、实数编码(浮点法编码)、多级参数编码、有序串编码,结构式编码等。
• 实数编码不必进行数值转换，可以直接在解的表现型上进行遗传算法操作。因此本案例采用该方法编码，每个染色体为一个实数向量。

2. 适应度函数

• 适应度函数是用来区分群体中个体好坏的标准，是进行自然选择的唯一依据，一般是由目标函数加以变换得到。
• 本案例是求函数的最小值，把函数值的倒数作为个体的适应度值。函数值越小的个体，适应度值越大，个体越优。

3. 选择操作

• 选择操作从旧群体中以一定概率选择优良个体组成新的种，以繁殖得到下一代个体。
• 个体被选中的概率跟适应度值有关，个体适应度值越高，被选中的概率越大。遗传算法选择操作有轮盘赌法、锦标赛法等多种方法，本案例选择轮盘赌法，即基于适应度比例的选择策略，个体i被选中的概率为
  
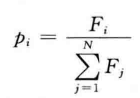
  其中，Fi为个体i的适应度值；N 为种群个体数目。

4. 交叉操作

• 交叉操作是指从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体。
• 由于个体采用实数编码,所以交叉操作采用实数交叉法,第k个染色体a_k,和第l个染色体a_l,在j位的交叉操作方法为
  
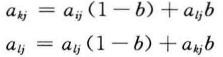
  其中,b是[0,1]区间的随机数。

5. 变异操作

• 变异操作的主要目的是维持种群多样性。
• 变异操作是从种群中随机选取一个个体,选择个体中的一点进行变异以产生更优秀的个体。第i个个体的第j个基因 a_ij进行变异的操作方法为
  
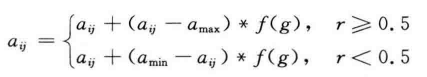
  其中,α_max是基因a_ij的上界;a_min是基因a_ij的下界;f(g)=r_2(1-g/G_max)^2,r_2是一个随机数,g是当前迭代次数,G_max是最大进化次数,r为[0,1]区间的随机数。

6. 非线性寻优

• 遗传算法迭代次数一次，以遗传算法当前计算的结果为初始值，采用MATLAB的线性规划函数fmincon进行局部寻优，并把寻找到的局部最优值作为新个体染色体继续进化

3 案例

3.1 题目

3.2 步骤

3.2.1 遗传算法参数设置

maxgen=30;                         %进化代数
sizepop=100;                       %种群规模
pcross=[0.6];                      %交叉概率
pmutation=[0.01];                  %变异概率
lenchrom=[1 1 1 1 1];              %变量字串长度
bound=[0 0.9*pi;0 0.9*pi;0 0.9*pi;0 0.9*pi;0 0.9*pi];  %变量范围

3.2.2 个体初始化

individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);  %种群结构体（适应度与染色体个体编码）
avgfitness=[];                                               %种群平均适应度
bestfitness=[];                                              %种群最佳适应度
bestchrom=[];                                                %适应度最好染色体
% 初始化种群（随机产生个体组成染色体）
for i=1:sizepop
    individuals.chrom(i,:)=Code(lenchrom,bound);       %随机产生个体
    x=individuals.chrom(i,:);
    individuals.fitness(i)=fun(x);                     %个体适应度（根据个体的编码确定适应度）在染色体中适应度就按函数的来
end
% 适应度在之后中按函数值越小，适应度越优，个体越优来排

%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:);  %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[];

• individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);：用结构体来承载染色体每个个体的适应度与其自身编码
• individuals.chrom(i,:)=Code(lenchrom,bound);：主函数中的语句，通过调用Code函数，可以随机生成染色体中的个体

Code函数

function ret=Code(lenchrom,bound)
flag=0;
while flag==0
    pick=rand(1,length(lenchrom));
    ret=bound(:,1)'+(bound(:,2)-bound(:,1))'.*pick; %线性插值
    flag=test(lenchrom,bound,ret);             %检验染色体的可行性
end

• 根据个体长度，随机产生数值，然后再通过线性插值确定个体中数值
• 通过调用test函数检验染色体是否在变量允许范围

test函数

function flag=test(lenchrom,bound,code)
flag=1;
[n,m]=size(code);

for i=1:n
    if code(i)<bound(i,1) || code(i)>bound(i,2)   %判断染色体的编码值是否在变量的取值范围内，如果不是则输出0
        flag=0;
    end
end

• 不断循环，直到染色体个体可行（即染色体的编码值都在变量的取值范围内）

fun函数

function y = fun(x)
y=-5*sin(x(1))*sin(x(2))*sin(x(3))*sin(x(4))*sin(x(5))-sin(5*x(1))*sin(5*x(2))*sin(5*x(3))*sin(5*x(4))*sin(5*x(5))+8;

• 在处理结构体中的适应度时按函数本身来计算，而不对函数直接做倒数等处理

3.2.3 历代处理

for i=1:maxgen

• 每次进行选择、交叉、变异的操作都会产生新的子代，然后以一代遍历完整作为真正的一代（子代）数据

a. 选择

individuals=Select(individuals,sizepop);
avgfitness=sum(individuals.fitness)/sizepop;    %染色体的平均适应度

• individuals=Select(individuals,sizepop);：主函数中的语句，调用Select函数进行选择操作，即选择操作从旧群体中以一定概率选择优良个体组成新的种，以繁殖得到下一代个体，依据是——个体被选中的概率跟适应度值有关，个体适应度值越高，被选中的概率越大

Select函数：轮盘赌法进行选择

function ret=Select(individuals,sizepop)
individuals.fitness= 1./(individuals.fitness);  % 取函数的倒数作为适应度
sumfitness=sum(individuals.fitness);
sumf=individuals.fitness./sumfitness;   % 基于适应度比例的选择函数
index=[];
% 轮盘赌法
for i=1:sizepop   %转sizepop次轮盘，对染色体中的每个个体进行选择
    pick=rand(1);
    while pick==0
        pick=rand(1);
    end
    for j=1:sizepop
        pick=pick-sumf(j);
        if pick<0
            index=[index j];
            break;  %寻找落入的区间，此次转轮盘选中了染色体i，注意：在转sizepop次轮盘的过程中，有可能会重复选择某些染色体
        end
    end
end
individuals.chrom=individuals.chrom(index,:);
individuals.fitness=individuals.fitness(index);
ret=individuals;

b. 交叉

• individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);：主函数中的语句，调用Cross函数进行交叉，即从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体

Cross函数：实数交叉法进行交叉

function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)
for i=1:sizepop 
    
    % 随机选择两个染色体进行交叉
    pick=rand(1,2);
    while prod(pick)==0
        pick=rand(1,2);
    end
    index=ceil(pick.*sizepop);
    % 交叉概率决定是否进行交叉
    pick=rand(1);
    while pick==0
        pick=rand(1);
    end
    if pick>pcross
        continue;
    end
    flag=0;
    while flag==0
        % 随机选择交叉位置
        pick=rand(1);
        while pick==0
            pick=rand(1);
        end
        pos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置，即选择第几个变量进行交叉，注意：两个染色体交叉的位置相同
        pick=rand(1); %交叉开始
        v1=chrom(index(1),pos);
        v2=chrom(index(2),pos);
        chrom(index(1),pos)=pick*v2+(1-pick)*v1;
        chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
        flag1=test(lenchrom,bound,chrom(index(1),:));  %检验染色体1的可行性
        flag2=test(lenchrom,bound,chrom(index(2),:));  %检验染色体2的可行性
        if   flag1*flag2==0
            flag=0;
        else
            flag=1;
        end    %如果两个染色体不是都可行，则重新交叉
    end
end
ret=chrom;

c. 变异

• individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,[i maxgen],bound);：主函数中的语句，调用Mutation函数进行变异，即从种群中随机选取一个个体,选择个体中的一点进行变异以产生更优秀的个体

Mutation函数

function ret=Mutation(pmutation,lenchrom,chrom,sizepop,pop,bound)
for i=1:sizepop  
    % 随机选择一个染色体进行变异
    pick=rand(1);
    while pick==0
        pick=rand(1);
    end
    index=ceil(pick*sizepop);
    % 变异概率决定该轮循环是否进行变异
    pick=rand(1);
    if pick>pmutation
        continue;
    end
    flag=0;
    while flag==0
        % 变异位置
        pick=rand(1);

        while pick==0
            pick=rand(1);
        end
        pos=ceil(pick*sum(lenchrom));  %随机选择了染色体变异的位置，即选择了第pos个变量进行变异
        v=chrom(i,pos);
        v1=v-bound(pos,1);
        v2=bound(pos,2)-v;
        pick=rand(1); %变异开始
        if pick>0.5
            delta=v2*(1-pick^((1-pop(1)/pop(2))^2));
            chrom(i,pos)=v+delta;
        else
            delta=v1*(1-pick^((1-pop(1)/pop(2))^2));
            chrom(i,pos)=v-delta;
        end   %变异结束
        flag=test(lenchrom,bound,chrom(i,:));     %检验染色体的可行性
    end
end
ret=chrom;

d. 非线性局部优化

if mod(i,10)==0
    individuals.chrom=nonlinear(individuals.chrom,sizepop);
end

• 当代次达到10的整数倍时，进行局部非线性优化

nonlinear函数 function ret = nonlinear(chrom,sizepop)

for i=1:sizepop x=fmincon(inline('-5*sin(x(1))*sin(x(2))*sin(x(3))*sin(x(4))sin(x(5))-sin(5x(1))sin(5x(2))sin(5x(3))sin(5x(4))sin(5x(5))'),chrom(i,:)',[],[],[],[],[0 0 0 0 0],[2.8274 2.8274 2.8274 2.8274 2.8274]); ret(i,:)=x'; end

e. 更新数据

• 更新当前代的适应度，并重新选出最小和最大适应度的染色体及它们在种群中的位置，即选出最优项

% 计算适应度
for j=1:sizepop
    x=individuals.chrom(j,:);
    individuals.fitness(j)=fun(x);
end

%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=min(individuals.fitness);
[worestfitness,worestindex]=max(individuals.fitness);
% 代替上一次进化中最好的染色体
if bestfitness>newbestfitness
    bestfitness=newbestfitness;
    bestchrom=individuals.chrom(newbestindex,:);
end
individuals.chrom(worestindex,:)=bestchrom;
individuals.fitness(worestindex)=bestfitness;

avgfitness=sum(individuals.fitness)/sizepop;

trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度

解

函数值：2.0000
变量：[1.5708 1.5708 1.5708 1.5708 1.5708]