遗传算法(基础) - ZYL-Harry/Mathematical_Modeling_Algorithms GitHub Wiki
1 遗传算法介绍
- 遗传算法(genetic algorithm,GA)是一种进化算法,其基本原理是仿效生物界中的“物竞天择、适者生存”的演化法则。遗传算法是把问题参数编码为染色体,再利用迭代的方式进行选择,交叉以及变异等运算来交换种群中染色体的信息,最终生成符合优化目标的染色体。
- 在遗传算法中,染色体对应的是数据或数组,通常是由一维的串结构数据来表示,串上各个位置对应基因的取值。基因组成的串就是染色体,或者称为基因型个体(individuals)。一定数量的个体组成了群体(population)。群体中个体的数目称为群体大小(population size),也称为群体规模。而各个个体对环境的适应程度叫做适应度(fitness)。
1.1 遗传算法的基本步骤
-
编码
遗传算法在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合便构成了不同的点。 -
初始群体的生成
- 随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了一个群体。遗传算法以这N个串结构数据作为初始点开始进化。
- 遗传算法工具箱中的函数——
crtbp:创建种群中创建任意离散随机种群的函数
创建种群函数——
crtbp
功能:创建任意离散随机种群
调用格式:
①[Chrom,Lind,BaseV] = crtbp(Nind,Lind)
②[Chrom,Lind,BaseV] = crtbp(Nind,Base)
③[Chrom,Lind,BaseV] = crthp(Nind,Lind,Base)
格式①创建一个大小为 Nind × Lind 的随机二进制矩阵,其中,Nind 为种群个体数,Lind为个体长度。返回种群编码 Chrom 和染色体基因位的基本字符向量 BaseV。
格式②创建一个种群个体为 Nind,个体的每位编码的进制数由 Base 决定(Base 的列数即为个体长度)。
格式③创建一个大小为 Nind× Lind 的随机矩阵,个体的各位的进制数由 Base 决定,这时输人参数 Lind 可省略(Base 的列数即为 Lind),即为格式②。
- 适应度评估
- 适应度表明个体或解的优劣性。不同的问题,适应性函数的定义方式也不同。
- 遗传算法工具箱中的函数——
ranking:适应度计算中基于排序的适应度分配的函数
适应度计算函数——
ranking
功能:基于排序的适应度分配
调用格式:
①FitnV = ranking(ObjV)
②FitnV = ranking(ObjV,RFun)
③FitnV = ranking(ObjV,RFun,SUBPOP)
格式①是按照个体的目标值 ObjV(列向量)由小到大的顺序对个体进行排序的,并返回个体适应度值 FitnV 的列向量。
格式②中 RFun 有三种情况:
(1)若 RFun 是一个在[1,2]区间内的标量,则采用线性排序,这个标量指定选择的压差。
(2)若 RFun 是一个具有两个参数的向量,则
RFun(2):指定排序方法,0 为线性排序,1 为非线性排序。
RFun(1):对线性排序,标量指定的选择压差 RFun(1)必须在[1,2]区间;对非线性排序,RFun(1)必须在[1,length(ObjV)-2]区间;如果为 NAN,则 RFun(1)假设为 2。
(3)若 RFun 是长度为length(ObjV)的向量,则它包含对每一行的适应度值计算。
格式③中的参数 ObjV 和 RFun 与格式①和格式②一致,参数 SUBPOP 是一个任选参数,指明在 ObjV 中子种群的数量。省略 SUBPOP 或 SUBPOP 为 NAN,则 SUBPOP=1。在[ObjV 中的所有子种群大小必须相同。如果 ranking 被调用于多子种群,则 ranking 独立地对每个子种群执行。
- 选择
- 选择的目的是为了从当前群体中选出优良的个体,使它们有机会作为父代为下一代繁殖子孙。遗传算法通过选择过程体现这一思想,进行选择的原则是适应性强的个体为下一代责献一个或多个后代的概率大。选择体现了达尔文的适者生存原则。
- 遗传算法工具箱中的函数——
select:选择函数中的高级选择例程函数
选择函数——
select
功能:从种群中选择个体(高级函数)
调用格式:
①SelCh = select(SEL_F,Chrom,FitnV)
②SelCh = select(SEL_F,Chrom,FitnV,GGAP)
③SelCh = select(SEL_F,Chrom,FitnV,GGAP,SUBPOP)
SEL_F 是一个字符串,包含一个低级选择函数名,如 rws 或 sus。
FitnV 是列向量,包含种群 Chrom 中个体的适应度值。这个适应度值表明了每个个体被选择的预期概率。
GGAP 是可选参数,指出了代沟部分种群被复制。如果 GGAP 省略或为 NAN,则 GGAP假设为 1.0。
SUBPOP 是一个可选参数,决定Chrom 中子种群的数量。如果 SUBPOP 省略或为NAN,则 SUBPOP=1。Chrom 中所有子种群必须有相同的大小。
- 交叉
- 交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体,新个体组合了其父辈个体的特性。交叉体现了信息交换的思想。
- 遗传算法工具箱中的函数——
recombin:交叉算子中的高级重组算子函数
交叉算子函数——
recombin
功能:重组个体(高级函数)
调用格式:
①NewChrom = recombin(REC_F,Chrpm)
②NewChrom = recombin(REC_F,Chrom,RecOpt)
③NewChrom - recombin(REC_F ,Chrom,RecOpt,SVEPOP)
recombin完成种群 Chrom 中个体的重组,在新种群 NewChrom 中返回重组后的个体。Chrom 和 NewChrom 中的一行对应一个个体。
REC_F 是一个包含低级重组函数名的字符串例如 recdis 或 xovsp。
RecOpt 是一个指明交叉概率的任选参数,如省略或为 NAN,将设为缺省值。
SUBPOP 是一个决定 Chrom 中子群个数的可选参数,如果省略或为 NAN,则 SUBPOP为1。Chrom 中的所有子种群必须有相同的大小。
- 变异
- 变异首先在群体中随机选择一个个体,对于选中的个体以一定的概率随机地改变串结构数据中某个串的值。同生物界一样,遗传算法中变异发生的概率很低,通常取值很小。
- 遗传算法工具箱中的函数——
mut:变异算子中的离散变异函数
变异算子函数——
mut
功能:离散变异算子
调用格式:
NewChrom = mut(OldChrom,Pm,BaseV)
OldChrom 为当前种群,Pm 为变异概率(省略时为 0.7/Lind),BaseV 指明染色体个体元素的变异的基本字符(省略时种群为二进制编码)。
- 其他函数
- 重插入函数——
reins
功能:重插入子代到种群中
调用格式:
①Chrom = reins(Chrom,SelCh)
②Chrom = reins(Chrom,SelCh,SUBPOP)
③Chrom - reins(Chrom,SelCh,SUBPOP,InsOpt,ObjVCh)
④[Chrom,ObjVCh]-reins(Chron,SelCh,SUBPOP,InsOpt,ObjVCh,ObjVSel)
reins 完成插人子代到当前种群,用子代代替父代并返回结果种群。Chrom 为父代种群,SelCh 为子代,每一行对应一个个体。
SUBPOP 是一个可选参数,指明 Chrom 和 SelCh 中子种群的个数。如果省略或者为NAN,则假设为 1。在 Chrom 和 SelCh 中每个子种群必须具有相同大小。
InsOpt 是一个最多有两个参数的任选向量。
InsOpt(1)是一个标量,指明用子代代替父代的方法。0 为均匀选择,子代代替父代使用均匀随机选择。1为基于适应度的选择,子代代替父代中适应度最小的个体。如果省略InsOpt(1)或 InsOpt(1)为 NAN,则假设为 0。
insOpt(2)是一个在[0,1]区间的标量,表示每个子种群中重插人的子代个体在整个子种群中个体的比率。如果 InsOpt(2)省略或为 NAN,则假设 InsOpt(2)=1.0。
ObjVCh 是一个可选列向量,包括 Chrom 中个体的目标值。对基于适应度的重插人,ObjVCh 是必需的。
ObjVSel 是一个可选参数,包含 SelCh 中个体的目标值。如果子代的数量大于重插人种群中的子代数量,则 ObjVSel 是必需的。这种情况子代将按它们的适应度大小选择插人。
- 实用函数——
bs2rv
功能:二进制到十进制的转换。
调用格式:
Pben =be2rv(Chrom,FieldD)
bs2rv 根据译码矩阵 FielaD 将二进制串矩阵 Chrom 转换为实值向量,返回十进制的矩阵。
矩阵 FieldD 有如下结构:
这个矩阵的组成如下:
- len 是包含在 Chrom 中的每个子串的长度,注意,sum(len)=size(Chrom,2)。
- lb 和 ub 分别是每个变量的下界和上界。
- code 指明子串是怎样编码的,1 为标准的二进制编码,0 为格雷编码。
- scale 指明每个子串所使用的刻度,0 表示算术刻度,1 表示对数刻度。
- lbin 和 ubin 指明表示范围中是否包含边界。0 表示不包含边界,1 表示包含边界。
1.2 基本遗传算法解决函数优化问题
1.2.1 简单一元函数优化
利用遗传算法计算函数的最小值:
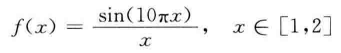
步骤
- 遗传算法参数设置
NIND=40; %种群大小
MAXGEN=20; %最大遗传代数
PRECI=20; %个体长度
GGAP=0.95; %代沟
px=0.7; %交叉概率
pm=0.01; %变异概率
trace=zeros(2,MAXGEN); %寻优结果的初始值,每代的(X,Y)坐标
FieldD=[PRECI;lb;ub;1;0;1;1]; %区域描述器
Chrom=crtbp(NIND,PRECI); %创建任意离散随机种群

- 优化
gen=0; %代计数器
X=bs2rv(Chrom,FieldD); %初始种群二进制到十进制转换
ObjV=sin(10* pi* X)./X; %计算目标函数值
while gen<MAXGEN
FitnV = ranking(ObjV); %分配适应度值
SelCh = select('sus',Chrom,FitnV,GGAP); %选择
SelCh = recombin('xovsp',SelCh,px); %交叉
SelCh = mut(SelCh,pm); %变异
X=bs2rv(SelCh,FieldD); %子代个体的十进制转换
ObjvSel=sin(10 * pi* X)./X; %计算子代的目标函数值
[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjvSel); %重插人子代到父代,得到新种群
X=bs2rv(Chrom,FieldD);
gen=gen+1; %代计数器增加1
%获取每代的最优解及其序号,Y 为最优解,I为个体的序号
[Y,I]= min(ObjV);
trace(1,gen)= X(I); %记下每代的最优值
trace(2,gen)=Y; %记下每代的最优值
end
- 先对初始的种群进行编码转换(二进制转十进制),并计算出相应的函数值
- 循环规定的代次,对每一代进行适应度分配、选择、交叉、变异操作从而生成新的子代个体,然后进行二进制转十进制并计算相应函数值,将其代入父代中得到新种群,然后找出目前进行的代中最优的一代解
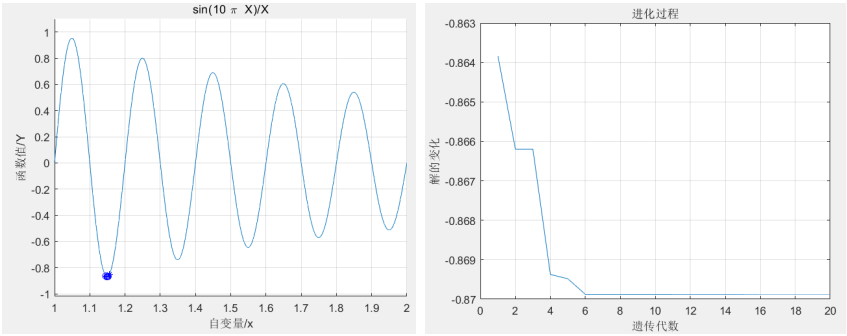
- 解
最优解:X=1.1489,Y=-0.86988
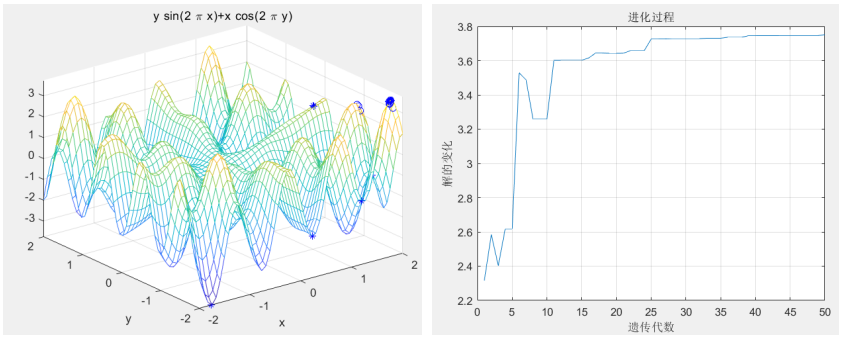
1.2.2 多元函数优化
利用遗传算法计算函数的最大值:
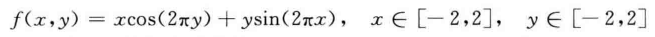
步骤
- 遗传算法参数设置
NIND=40; %个体数目
MAXGEN=50; %最大遗传代数
PRECI=20; %变量的二进制位数
GGAP=0.95; %代沟
px=0.7; %交叉概率
pm=0.01; %变异概率
trace=zeros(3,MAXGEN); %寻优结果的初始值,(X,Y,Z)
FieldD=[PRECI PRECI;lbx lby;ubx uby;1 1;0 0;1 1;1 1]; %区域描述器
Chrom=crtbp(NIND,PRECI*2); %初始种群

- 优化
gen=0; %代计数器
XY=bs2rv(Chrom,FieldD); %计算初始种群的十进制转换
X=XY(:,1);Y=XY(:,2);
ObjV=Y.*sin(2*pi*X)+X.*cos(2*pi*Y); %计算目标函数值
while gen<MAXGEN
FitnV=ranking(-ObjV); %分配适应度值
SelCh=select('sus',Chrom,FitnV,GGAP); %选择
SelCh=recombin('xovsp',SelCh,px); %重组
SelCh=mut(SelCh,pm); %变异
XY=bs2rv(SelCh,FieldD); %子代个体的十进制转换
X=XY(:,1);Y=XY(:,2);
ObjVSel=Y.*sin(2*pi*X)+X.*cos(2*pi*Y); %计算子代的目标函数值
[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代,得到新种群
XY=bs2rv(Chrom,FieldD);
gen=gen+1; %代计数器增加
%获取每代的最优解及其序号,Y为最优解,I为个体的序号
[Y,I]=max(ObjV);
trace(1:2,gen)=XY(I,:); %记下每代的最优值
trace(3,gen)=Y; %记下每代的最优值
end
- 先对初始的种群进行编码转换(二进制转十进制),并计算出相应的函数值
- 循环规定的代次,对每一代进行适应度分配、选择、交叉、变异操作从而生成新的子代个体,然后进行二进制转十进制并计算相应函数值,将其代入父代中得到新种群,然后找出目前进行的代中最优的一代解
- 解
最优解:X=1.7624,Y=-1.9961,Z=3.7519