禁忌搜索算法介绍

1. 爬山算法：
   从当前的节点开始，和周围的邻居节点的值进行比较。 如果当前节点是最大的，那么返回当前节点，作为最大值 (既山峰最高点)；反之就用最高的邻居节点来，替换当前节点，从而实现向山峰的高处攀爬的目的。如此循环直到达到最高点。因为不是全面搜索，所以结果可能不是最佳。
2. 局部搜索算法：
   从爬山法改进而来的。局部搜索算法的基本思想：在搜索过程中，始终选择当前点的邻居中与离目标最近者的方向搜索。同样，局部搜索得到的解不一定是最优解。
3. 禁忌搜索算法——仿人智能算法：
   禁忌（Tabu Search）算法是一种亚启发式(meta-heuristic)随机搜索算法，它从一个初始可行解出发，选择一系列的特定搜索方向（移动）作为试探，选择实现让特定的目标函数值变化最多的移动。为了避免陷入局部最优解，TS搜索中采用了一种灵活的“记忆”技术，对已经进行的优化过程进行记录和选择，指导下一步的搜索方向，这就是Tabu表的建立。

• 网上的例子：
  为了找出地球上最高的山，一群有志气的兔子们开始想办法：
  a. 爬山算法
  兔子朝着比现在高的地方跳去。他们找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山法，它不能保证局部最优值就是全局最优值。
  b. 禁忌搜索算法
  兔子们知道一个兔的力量是渺小的。他们互相转告着，哪里的山已经找过，并且找过的每一座山他们都留下一只兔子做记号。他们制定了下一步去哪里寻找的策略。这就是禁忌搜索。
• 学习总结：禁忌搜索应该就是先局部搜索得到最优解然后记录这个最优解（放入禁忌表中），接下来再进行局部搜索然后同样记录一个最优解（放入禁忌表中），······以此类推，迭代数次，得到最优解

相关概念

1. 邻域
   官方一点：所谓邻域，简单的说即是给定点附近其他点的集合。在距离空间中，邻域一般被定义为以给定点为圆心的一个圆；而在组合优化问题中，邻域一般定义为由给定转化规则对给定的问题域上每结点进行转化所得到的问题域上结点的集合。
   通俗一点：邻域就是指对当前解进行一个操作(这个操作可以称之为邻域动作)可以得到的所有解的集合。那么邻域的本质区别就在于邻域动作的不同了。

2. 邻域动作
   邻域动作是一个函数，通过这个函数，对当前解s，产生其相应的邻居解集合。例如：对于一个bool型问题，其当前解为：s = 1001，当将邻域动作定义为翻转其中一个bit时，得到的邻居解的集合N(s)={0001,1101,1011,1000}，其中N(s) ∈ S。同理，当将邻域动作定义为互换相邻bit时，得到的邻居解的集合N(s)={0101,1001,1010}。

3. 禁忌表
   包括禁忌对象和禁忌长度。（当兔子们再寻找的时候，一般地会有意识地避开泰山，因为他们知道，这里已经找过，并且有一只兔子在那里看着了。这就是禁忌搜索中“禁忌表（tabu list）”的含义。）

4. 侯选集合
   侯选集合由邻域中的邻居组成。常规的方法是从邻域中选择若干个目标值或评价值最佳的邻居入选。

5. 禁忌对象
   禁忌算法中，由于我们要避免一些操作的重复进行，就要将一些元素放到禁忌表中以禁止对这些元素进行操作，这些元素就是我们指的禁忌对象。（当兔子们再寻找的时候，一般地会有意识地避开泰山，因为这里找过了。并且还有一只兔子在这留守。）

6. 禁忌长度
   禁忌长度是被禁对象不允许选取的迭代次数。一般是给被禁对象x一个数（禁忌长度） t ，要求对象x 在t 步迭代内被禁，在禁忌表中采用tabu(x)=t记忆，每迭代一步，该项指标做运算tabu(x)=t−1，直到tabu(x)=0时解禁。于是，我们可将所有元素分成两类，被禁元素和自由元素。禁忌长度t 的选取可以有多种方法，例如t=常数，或t=[√n]，其中n为邻域中邻居的个数；这种规则容易在算法中实现。
   （那只留在泰山的兔子一般不会就安家在那里了，它会在一定时间后重新回到找最高峰的大军，因为这个时候已经有了许多新的消息，泰山毕竟也有一个不错的高度，需要重新考虑，这个归队时间，在禁忌搜索里面叫做“禁忌长度（tabu length）”。）

7. 评价函数
   评价函数是侯选集合元素选取的一个评价公式，侯选集合的元素通过评价函数值来选取。以目标函数作为评价函数是比较容易理解的。目标值是一个非常直观的指标，但有时为了方便或易于计算，会采用其他函数来取代目标函数。

8. 特赦规则
   在禁忌搜索算法的迭代过程中，会出现侯选集中的全部对象都被禁忌，或有一对象被禁，但若解禁则其目标值将有非常大的下降情况。在这样的情况下，为了达到全局最优，我们会让一些禁忌对象重新可选。这种方法称为特赦，相应的规则称为特赦规则。
   （如果在搜索的过程中，留守泰山的兔子还没有归队，但是找到的地方全是华北平原等比较低的地方，兔子们就不得不再次考虑选中泰山，也就是说，当一个有兔子留守的地方优越性太突出，超过了“best so far”的状态，就可以不顾及有没有兔子留守，都把这个地方考虑进来，这就叫“特赦准则（aspiration criterion）”。）

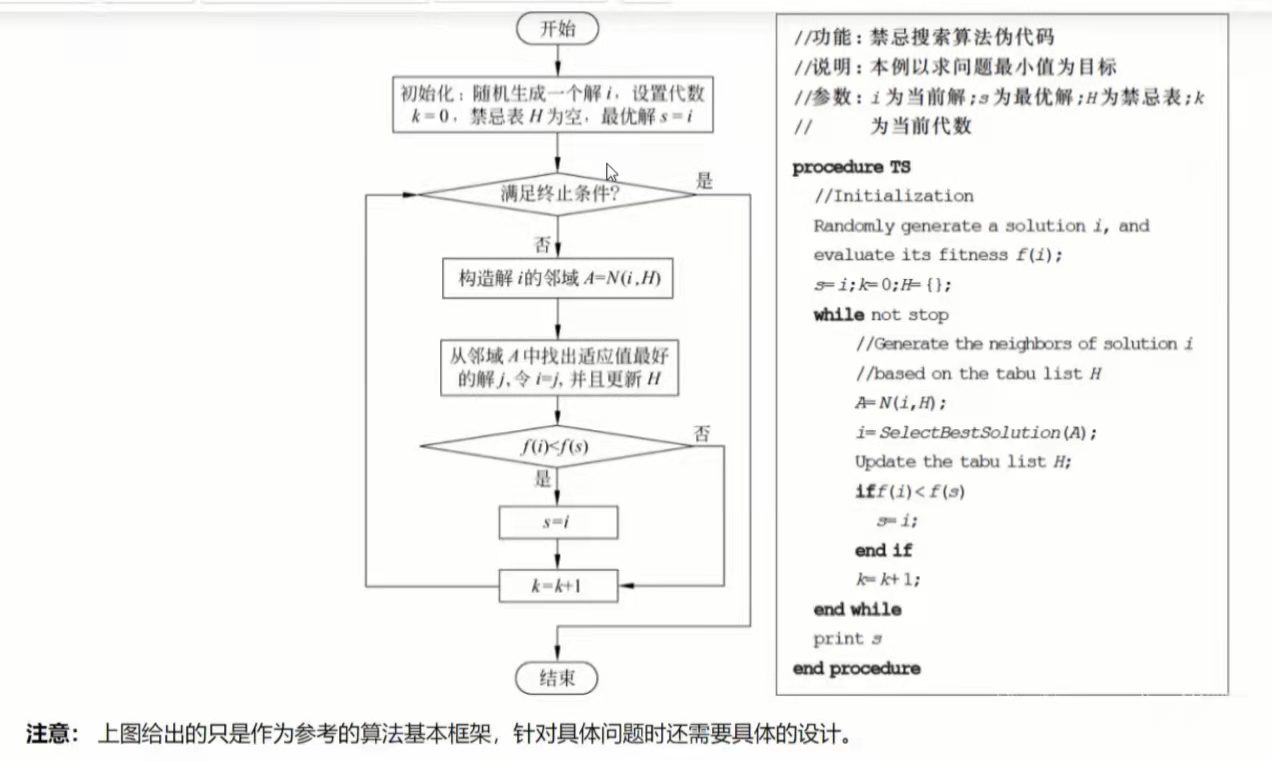
基本流程图

\

• 注意：流程图中仅给出了算法的基本框架，对于具体问题需要具体分析

Python代码解决TSP问题

1. 初始化参数

# 参数
CityNum = 20  # 城市数量
MinCoordinate = 0  # 二维坐标最小值
MaxCoordinate = 101  # 二维坐标最大值

# TS参数
tabu_limit = 50  # 禁忌长度，该值定义时应小于(CityNum*(CityNum-1)/2）
iterMax = 200  # 迭代次数
traversalMax = 100  # 每一代局部搜索次数

tabu_list = []  # 禁忌表
tabu_time = []  # 禁忌次数
best_value = math.pow(10, 10)  # 较大的初始值，用于存储最优解
best_line = []  # 存储最优路径

• 对TSP问题的城市数量、禁忌搜索相关参数（包括禁忌表、禁忌表长度、最优路径及其距离）进行初始化

2. 生成城市列表

# 随机生成城市数据,城市序号为0,1,2,3...
    CityCoordinates = [(random.randint(MinCoordinate, MaxCoordinate), random.randint(MinCoordinate, MaxCoordinate)) for
                       i in range(CityNum)]

3. 计算城市列表中各城市间的距离

# 计算城市之间的距离
    dis_matrix = pd.DataFrame(data=None, columns=range(len(CityCoordinates)), index=range(len(CityCoordinates)))
    for i in range(len(CityCoordinates)):
        xi, yi = CityCoordinates[i][0], CityCoordinates[i][1]
        for j in range(len(CityCoordinates)):
            xj, yj = CityCoordinates[j][0], CityCoordinates[j][1]
            dis_matrix.iloc[i, j] = round(math.sqrt((xi - xj) ** 2 + (yi - yj) ** 2), 2)

4. 用贪婪算法得到最初的最优路径解

a. 主函数部分

# 贪婪构造
    line = greedy(CityCoordinates, dis_matrix)  # 用贪婪算法得到最短路径
    value = calFitness(line, dis_matrix)        # 初始路径距离

• 主函数中调用greedy函数来得到有贪婪算法解得初始的最优路径
• 主函数中调用calFitness函数来得到初始的最优路径的总距离

b. greedy函数：用贪婪算法得到初始的最优路径

def greedy(CityCoordinates, dis_matrix):
    '''贪婪策略构造初始解'''
    # 出来dis_matrix
    dis_matrix = dis_matrix.astype('float64')
    for i in range(len(CityCoordinates)):
        dis_matrix.loc[i, i] = math.pow(10, 10)     # 将自己与自己的距离定义为一个极大的数
    line = []  # 初始化
    now_city = random.randint(0, len(CityCoordinates) - 1)  # 随机生成出发城市
    line.append(now_city)  # 添加当前城市到路径
    dis_matrix.loc[:, now_city] = math.pow(10, 10)  # 更新距离矩阵(使该城市所在列为一个极大的数)，已经过城市不再被取出
    for i in range(len(CityCoordinates) - 1):
        next_city = dis_matrix.loc[now_city, :].idxmin()  # 在该城市所在行中寻找值最小的城市，即与其距离最近的城市
        line.append(next_city)  # 添加进路径
        dis_matrix.loc[:, next_city] = math.pow(10, 10)  # 更新距离矩阵（使该城市所在列为一个极大的数）
        now_city = next_city  # 更新当前城市
    return line     # 返回贪婪算法获得的最短路径

• 随机选定触发的城市，然后通过不断地逐行比较得到距离最小的城市从而得到最短路径

c. calFitness函数：由路径得到路径的总距离（评价函数）

# 计算路径距离，即评价函数
def calFitness(line, dis_matrix):
    dis_sum = 0
    dis = 0
    for i in range(len(line)):  # 0,1,2,...,19
        if i < len(line) - 1:   # i<19：算节点与下一个节点的距离；i=19：算节点与最初点的距离:
            dis = dis_matrix.loc[line[i], line[i + 1]]  # 计算距离
            dis_sum = dis_sum + dis
        else:
            dis = dis_matrix.loc[line[i], line[0]]
            dis_sum = dis_sum + dis
    return round(dis_sum, 1)    # 返回路径距离

• 通过逐个点可以计算出路径的总距离
• TSP问题中路径的长度就可以作为禁忌搜索算法中的评价函数

5. 存储初始化后的最优解

best_value, best_line = value, line
draw_path(best_line, CityCoordinates)
best_value_list = []
best_value_list.append(best_value)

• 将由贪婪算法得到的最优路径先行作为最优解存储起来

6. 首次更新禁忌表

tabu_list.append(line)          # 将贪婪算法所得到的的最初的最短路径先放入禁忌表中
tabu_time.append(tabu_limit)    # 初始化禁忌次数

• 将贪婪算法所得到的的最初的最短路径先放入禁忌表中（存储记忆），使得之后不再探索该路径
• 初始化禁忌次数

7. 进行循环搜索

itera = 0  # 已进行迭代的次数
while itera <= iterMax:
    new_value, new_line = traversal_search(line, dis_matrix, tabu_list)     # 遍历搜索——获得局部搜索后得到的最短路径（最优解）
    if new_value < best_value:  # 判断新获得的最优解是否优于本来的最优解
        best_value, best_line = new_value, new_line  # 更新最优解
        best_value_list.append(best_value)
    line, value = new_line, new_value  # 更新当前解

    # 更新禁忌表：如果禁忌次数到0了，则意味着禁忌表中的第一个元素可以解禁了
    tabu_time = [x - 1 for x in tabu_time]
    if 0 in tabu_time:
        tabu_list.remove(tabu_list[tabu_time.index(0)])
        tabu_time.remove(0)
    tabu_list.append(line)  # 把当前最优解放入禁忌表中作为已经探索过的路径，接下来非特殊情况就不再对该路径重复探索
    tabu_time.append(tabu_limit)    # 重新初始化禁忌次数
    itera += 1
'''
经过这样的循环后便可以获得迭代200次且每次局部都进行100次搜索的最优解
'''

a. 通过遍历获取依次迭代的最优解

new_value, new_line = traversal_search(line, dis_matrix, tabu_list)     # 遍历搜索——获得局部搜索后得到的最短路径（最优解）
if new_value < best_value:  # 判断新获得的最优解是否优于本来的最优解
    best_value, best_line = new_value, new_line  # 更新最优解
    best_value_list.append(best_value)
line, value = new_line, new_value  # 更新当前解

• 使用traversal_search函数，通过遍历进行局部搜索得到一次迭代的最优解

def traversal_search(line, dis_matrix, tabu_list):
    '''邻域随机遍历搜索'''
    traversal = 0  # 搜索次数
    traversal_list = []  # 存储局部搜索生成的解,也充当局部禁忌表
    traversal_value = []  # 存储局部解对应路径距离
    while traversal <= traversalMax:    # 局部进行traversalMax次搜索（100次）
        pos1, pos2 = random.randint(0, len(line) - 1), random.randint(0, len(line) - 1)  # 交换点：随即从城市中选择两个城市
        # 复制当前路径，并交换生成新路径
        new_line = line.copy()
        new_line[pos1], new_line[pos2] = new_line[pos2], new_line[pos1]     # 在新路径中将随机选出的两个城市进行交换
        new_value = calFitness(new_line, dis_matrix)  # 当前路径距离
        # 新生成路径不在局部禁忌表和全局禁忌表中，为有效搜索，否则重新继续搜索
        if (new_line not in traversal_list) & (new_line not in tabu_list):
            traversal_list.append(new_line)
            traversal_value.append(new_value)
            traversal += 1
    return min(traversal_value), traversal_list[traversal_value.index(min(traversal_value))]    # 返回局部搜索后路径距离最短的路线及其距离

• 在局部进行100次的搜索，每次搜索将路线中的随机两个城市进行交换，然后判断其是否在局部禁忌表和全局禁忌表中，如果不是则将其放入局部禁忌表中防止接下来局部搜索时重复放入
• 有想法：可以直接将得到的新路线其放入全局禁忌表中，不过考虑到禁忌表长度限制，所以只放入局部禁忌表中，而全局禁忌表仅放那些局部遍历的最优解
• 禁忌搜索应该就是先局部搜索得到最优解然后记录这个最优解，接下来再进行局部搜索然后同样记录一个最优解，······以此类推，迭代数次，得到最优解

b. 更新禁忌表

# 更新禁忌表：如果禁忌次数到0了，则意味着禁忌表中的第一个元素可以解禁了
        tabu_time = [x - 1 for x in tabu_time]
        if 0 in tabu_time:
            tabu_list.remove(tabu_list[tabu_time.index(0)])
            tabu_time.remove(0)
        tabu_list.append(line)  # 把当前最优解放入禁忌表中作为已经探索过的路径，接下来非特殊情况就不再对该路径重复探索
        tabu_time.append(tabu_limit)    # 重新初始化禁忌次数
        itera += 1

• 如果禁忌次数（禁忌表长度）达到则解禁一个并初始化禁忌次数

8. 输出结果

# 路径顺序
print(best_line)
print(best_value)

# 画路径图
draw_path(best_line, CityCoordinates)

9. 程序效果

• 生成的城市列表：

[(50, 14), (24, 82), (36, 39), (39, 100), (56, 36),
 (2, 7), (10, 78), (27, 64), (74, 68), (100, 17), 
 (51, 22), (77, 68), (43, 61), (101, 53), (10, 90),
 (16, 4), (59, 66), (39, 92), (47, 4), (65, 89)]

• 贪婪算法得到的最短路径图：
  
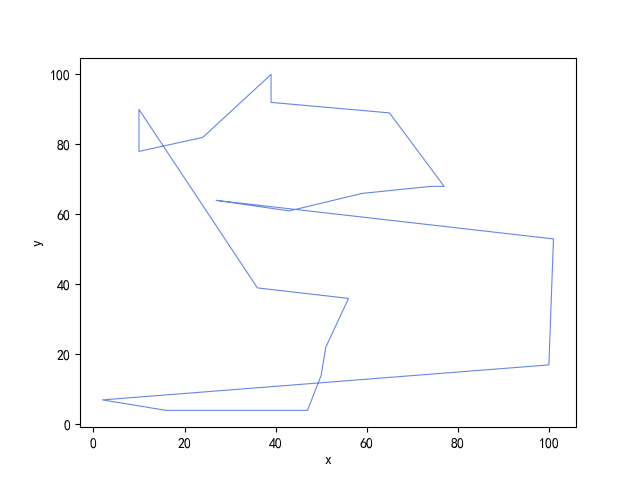
• 禁忌搜索算法得到的最优路径：[13, 11, 8, 16, 12, 19, 3, 17, 1, 14, 6, 7, 2, 5, 15, 18, 0, 10, 4, 9]
• 禁忌搜索算法得到的最优路径的距离：439.1
• 禁忌搜索算法得到的最优路径的路径图：